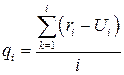|
|
Временные характеристики работ
В таблице временных характеристик работ приняты следующие обозначения: t(i,j)-продолжительность работы tpн -ранний срок начала работы tpo -ранний срок окончания работы tnн -поздний срок начала работы tnо -поздний срок окончания работы Rпол-полный резерв времени работы R1 -резерв времени первого рода (резерв времени увеличения продолжительности работы без изменения позднего срока начального события) R2 -резерв времени второго рода (резерв времени увеличения продолжительности работы без изменения раннего срока конечного события). Задача № 4 Распределение капиталовложений Найти оптимальное распределение капиталовложений в модернизацию производства между четырьмя предприятиями так, чтобы общий прирост продукции был максимальным. Исходные данные по каждому предприятию (прирост выпуска продукции
Таблица исходных данных задачи
Данная задача динамического программирования. Оптимальное управление строится поэтапно шаг за шагом. На каждом этапе оптимизируется управление только этого шага, но оно должно быть оптимальным с точки зрения процесса в целом. Каковы бы ни были начальное состояние системы на любом шаге и управление, выбранное на данном шаге, последующие управления должны выбираться оптимальными относительно состояния, к которому придет система в конце данного шага.
Шаг 1.Пусть все средства выделены первым двум предприятиям. Расчет прироста выпуска продукции в результате капиталовложений в модернизацию производства только первых двух предприятий будем производить в таб.№1.
Шаг 2. Пусть все средства выделены первым трем предприятиям. Расчет прироста выпуска продукции в результате капиталовложений в модернизацию производства только первых трех предприятий будем производить в таб.№2.
Шаг 3.Пусть средства выделены всем четырем предприятиям. Расчет прироста выпуска продукции в результате капиталовложений в модернизацию производства всех четырех предприятий будем производить в таб.№3.
Таким образом, при оптимальном распределении капиталовложений между предприятиями в зависимости от объема инвестиций (20, 40, 60, 80, 100 тыс. грн) прирост производства может составить 18, 36, 54, 72 или 90 единиц.
Задача №5 Матричная игра Методами линейного программирования найти решение матричной игры (найти оптимальные смешенные стратегии игроков) с платежной матрицей. Условие приведено в таблице:
В конфликтной ситуации столкнулись противоположные интересы двух сторон – A и B. Сторона A имеет три стратегии поведения в этой ситуации. Эти стратегии обозначены Цель первого игрока А обеспечить себе максимальный выигрыш при применении против него игроком В своей оптимальной стратегии. Цель второго игрока В – обеспечить минимальный проигрыш при применением игроком А своей оптимальной стратегии. Игрок А стремится выбором стратегии
Это нижняя цена игры, или гарантированный выигрыш игрока А. Игрок В выбирает такую стратегию
Пусть V – цена игры (выигрыш одного и равный ему проигрыш другого). и Если Если Решение Найдём нижнюю и верхнюю цену игры:
Так как
Переходим к канонической форме записи системы:
Разделим каждое из уравнений полученной системы на V и введём обозначения: Выражение
Решаем эту систему симплексным методом с помощью симплекс таблицы.
Так как в индексной строке третьей итерации нет отрицательных значений, то получен оптимальный план для переменной
Из принятых обозначений находим:
Оптимальная стратегия первого игрока: Одновременно с определением оптимальной стратегии игрока А найдена и оптимальная стратегия игрока В. Его стратегия отражена в индексной строке под переменными
Задача № 6 Замена оборудования Определить оптимальные сроки замены оборудования за плановый период n=10 лет, эксплуатировавшийся к началу планового периода t=8 лет, если стоимость нового оборудования составляет р=14, остаточная стоимость S(t)=2, стоимость продукции, произведенной за год r(t) и ежегодные расходы на эксплуатацию оборудования U(t) приведены в таблице: (i - срок эксплуатации; лет).
Определим затраты на приобретение нового оборудования:
Прибыль от эксплуатации нового оборудования за первый год с учётом затрат на его приобретение:
Прибыль от эксплуатации оборудования за i -й год: Средняя прибыль от эксплуатации вновь установленного оборудования за i лет:
Результаты расчёта прибыли приведены в таблице:
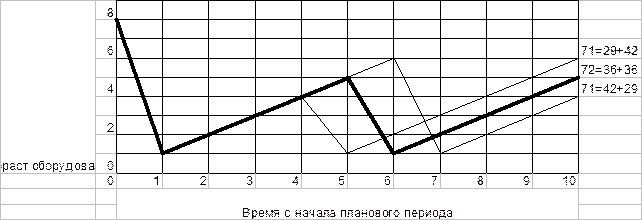
Cтроим график среднегодовой прибыли от эксплуатации оборудования i лет:
Так как среднегодовая прибыль максимальна при сроке эксплуатации оборудования 4 года, то оборудование имеет смысл заменять только после четырёх- шести лет его службы, чтобы обеспечить максимальную прибыль за плановый период. Так как возраст оборудования на начало планового периода превышает 4 года (восемь лет), то с начала первого года планового периода заменяем оборудование новым. Эксплуатируем это оборудование в течение пяти лет, снова заменяем его новым и снова эксплуатируем пять лет до окончания планового периода. Суммарная прибыль от использования оборудования в таком режиме составит 72 денежных единицы. Это максимально достижимая прибыль. При эксплуатации оборудования после замены четыре года, замены новым и эксплуатации второго нового оборудования уже в течении шести лет до окончания планового периода прибыль составит 71 денежную единицу. Такой же будет прибыль при эксплуатации оборудования в течении шести и четырёх лет соответственно.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 в зависимости от выделенных средств
в зависимости от выделенных средств  , (тыс. грн.) на реконструкцию и модернизацию) приведены в таблице.
, (тыс. грн.) на реконструкцию и модернизацию) приведены в таблице.









 , а стороной В стратегии
, а стороной В стратегии  выигрыш стороны А будет
выигрыш стороны А будет  . Для стороны В такой же по величине будет проигрыш. Эти значения приведены в платежной матрице. Для удобства вычислений в этой матрице все
. Для стороны В такой же по величине будет проигрыш. Эти значения приведены в платежной матрице. Для удобства вычислений в этой матрице все  . Если бы среди них были и отрицательные значения, то прибавлением ко всем элементам матрицы наибольшего по модулю отрицательного числа матрица переводится в положительно определенную.
. Если бы среди них были и отрицательные значения, то прибавлением ко всем элементам матрицы наибольшего по модулю отрицательного числа матрица переводится в положительно определенную. .
. :
: .
. .
. =
=  . Тогда интересы обоих игроков будут максимально удовлетворены, если игрок А выбирает стратегию
. Тогда интересы обоих игроков будут максимально удовлетворены, если игрок А выбирает стратегию  и
и  .
.

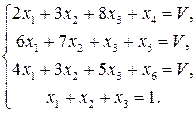





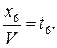
 будем рассматривать как целевую функцию, которая должна достигать максимума. Имеем стандартную задачу линейного программирования:
будем рассматривать как целевую функцию, которая должна достигать максимума. Имеем стандартную задачу линейного программирования: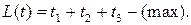
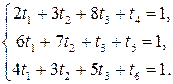

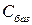










 .
.
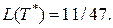
 - цена игры.
- цена игры. - относительная частота применения стратегии
- относительная частота применения стратегии 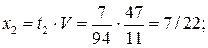 - относительная частота применения стратегии
- относительная частота применения стратегии  - относительная частота применения стратегии
- относительная частота применения стратегии 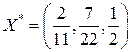
 Переменные
Переменные  , умноженные на цену игры V, представляют собой относительные частоты применения стратегий С1,С2,С3. Y*=(6/11;1/11;4/11).
, умноженные на цену игры V, представляют собой относительные частоты применения стратегий С1,С2,С3. Y*=(6/11;1/11;4/11). 14 – 2 = 12
14 – 2 = 12 25 - 13 – 12 = 0
25 - 13 – 12 = 0 .
.