|
|
Решения задач 2.1 – 2.3 диагностической работы2.1. Решение. Пусть O – центр нижнего основания призмы. Прямая BO параллельна AF. Так как плоскости ABC и BCC1перпендикулярны, то искомым углом будет угол OBC. Так как треугольник OBC равносторонний, то этот угол будет равен 60о.
Ответ. 60о.
2.2. Решение. Так как прямые BB1 и CC1 параллельны, то искомый угол будет равен углу между прямой BB1 и плоскостью BDE1. Прямая BD, через которую проходит плоскость BDE1, перпендикулярна плоскости ABB1 и, значит, плоскость BDE1 перпендикулярна плоскости ABB1. Следовательно, искомый угол будет равен углу A1BB1, т.е. равен 45о.
Ответ. 45о.
2.3. Решение. Через вершину S проведем прямую, параллельную прямой AB, и отложим на ней отрезок SF, равный отрезку AB. В тетраэдре SBCF все ребра равны 1 и плоскость BCF параллельна плоскости SAD. Перпендикуляр EH, опущенный из точки E на плоскость BCF, равен половине высоты тетраэдра, т.е. равен
Ответ.
Тренировочная работа 2. Угол между прямой и плоскостью
1. В кубе A…D1найдите тангенс угла между прямой AC1 и плоскостью BDD1.
2. В кубе A…D1найдите синус угла между прямой AB и плоскостью CB1D1.
3. В правильном тетраэдре ABCD точка E – середина ребра BD.Найдите синус угла между прямой AE и плоскостью ABC.
4. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между прямой BB1и плоскостью
AB1C1.
5. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BD и плоскостью SBC.
6. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите синус угла между прямой BC и плоскостью SAF.
7. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой AA1и плоскостью BCE1.
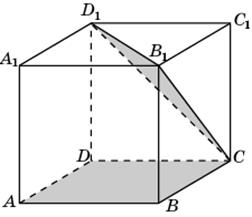
8. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите синус угла между прямой BC1и плоскостью AFF1.
Решения задач 3.1 – 3.3 диагностической работы
3.1. Первое решение. Так как плоскость FCC1 параллельна плоскости DEE1, то искомый угол равен углу между плоскостями AFF1 и FCC1. Так как плоскости AFF1 и FCC1 перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол AFC, который равен 60о. Второе решение. Так как плоскость AFF1 параллельна плоскости BEE1, то искомый угол равен углу между плоскостями BEE1 и DEE1. Так как плоскости BEE1 и DEE1 перпендикулярны плоскости ABC, то соответствующим линейным углом будет угол BED, который равен 60о.
Ответ. 60о. 3.2. Решение. Так как плоскость ADD1 параллельна плоскости BCC1, то искомый угол равен углу между плоскостями BCC1 и BDC1. Пусть E – середина отрезка BC1. Тогда прямые CE и DE будут перпендикулярны прямой BC1 и, следовательно,угол CED будет линейным углом между плоскостями BCC1 и BDC1. Треугольник CED прямоугольный, катет CD равен 1, катет CE равен
Ответ.
3.3. Пусть DE – линия пересечения данных плоскостей, F – середина отрезка DE, G – середина отрезка A1C1. Угол GFB1 является линейным углом между данными плоскостями. В треугольнике GFB1 имеем: FG = FB1 =
Ответ. Тренировочная работа 3. Угол между двумя плоскостями
1. В кубе A…D1найдите тангенс угла между плоскостями ABC и CB1D1.
2. В кубе A…D1найдите косинус угла между плоскостями B A1C1 и AB1D1.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и CA1B1.
4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус угла между плоскостями S
AD и SBC.
5. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите косинус двугранного угла, образованного гранями SBC и SCD.
6. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SBC и SEF.
7. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между плоскостями SAF и SBC.
8. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите тангенс угла между плоскостями ABC и DB1F1.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 . Угол между прямой BE и плоскостью SAD равен углу EBH, синус которого равен
. Угол между прямой BE и плоскостью SAD равен углу EBH, синус которого равен 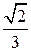 .
.
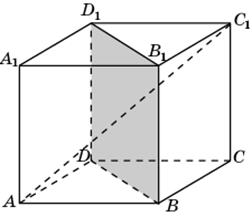









 . Следовательно,
. Следовательно,  .
.
 .
. , GB1 =
, GB1 =  . По теореме косинусов находим
. По теореме косинусов находим  .
.
 .
.