|
|
Тренировочная работа 1. Угол между прямымиДиагностическая работа
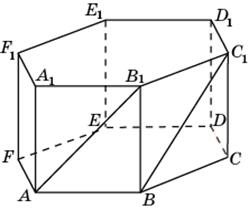
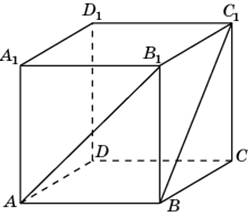
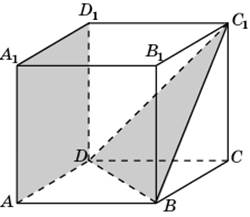
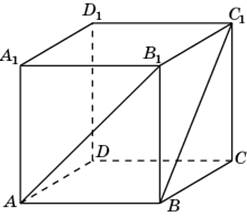
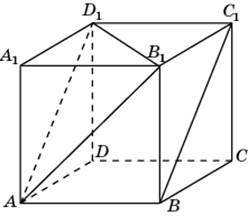
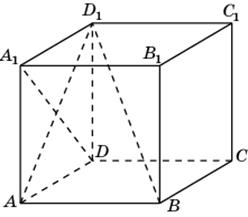
1.1.В единичном кубе A…D1 найдите угол между прямыми AB1 и BC1.
1.2.В единичном кубе A…D1 найдите угол между прямыми DA1и BD1.
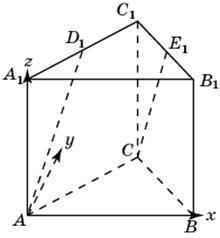
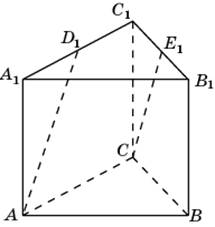
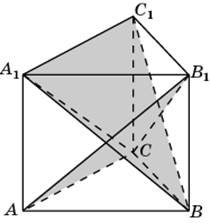
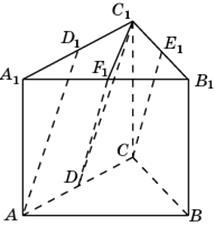
1.3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AD1 и CE1, где D1 и E1 – соответственно середины ребер A1C1 и B1C1.
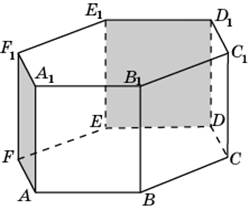
2.1.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой AF и плоскостью BCC1.
2.2. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между прямой CC1и плоскостью BDE1.
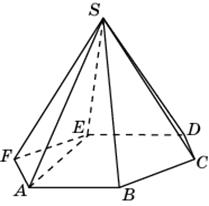
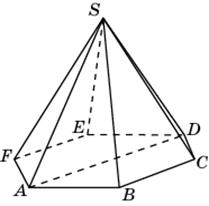
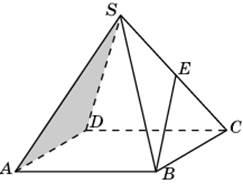
2.3. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите синус угла между прямой BE и плоскостью SAD, где E – середина ребра SC.
3.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите угол между плоскостями AFF1 и DEE1.
3.2. В единичном кубе A…D1найдите тангенс угла между плоскостями
ADD1 и BDC1.
3.3. В правильной треугольной призме ABCA1B1C1D1, все ребра которой равны 1, найдите косинус угла между плоскостями ACB1 и BA1C1.
4.1. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до прямой D1F1.
4.2. В единичном кубе A…D1 найдите расстояние от точки A до прямой BD1.
4.3.В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки F до прямой BG, где G – середина ребра SC.
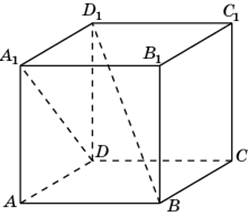
5.1. В единичном кубе A…D1 найдите расстояние от точки A до плоскости BDA1.
5.2. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки A до плоскости SBC.
5.3.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние от точки A до плоскости BFE1.
6.1.В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, найдите расстояние между прямыми SA и BC.
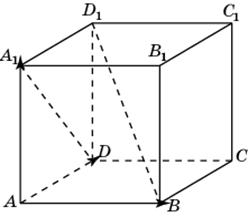
6.2. В единичном кубе A…D1 найдите расстояние между прямыми AB1и BC1.
6.3.В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите расстояние между прямыми AA1и CF1.
Решения задач 1.1 – 1.3 диагностической работы
1.1. Первое решение. Прямая AD1 параллельна прямой BC1 и, следовательно, угол между прямыми AB1 и BC1 равен углу B1AD1. Треугольник B1AD1равносторонний и, значит, угол B1AD1 равен 60о.
Второе решение. Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1. Вектор
Ответ. 60о.
1.2. Первое решение. Рассмотрим ортогональную проекцию AD1 прямой BD1 на плоскость ADD1. Прямые AD1 и DA1 перпендикулярны. Из теоремы о трех перпендикулярах следует, что прямые DA1 и BD1 также перпендикулярны, т.е. искомый угол между прямыми DA1 и BD1 равен 90о.
Второе решение. Введем систему координат, считая началом координат точку A, осями координат – прямые AB, AD, AA1. Вектор  имеет координаты (0, -1, 1). Вектор имеет координаты (0, -1, 1). Вектор 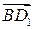 имеет координаты (-1, 1, 1). Скалярное произведение этих векторов равно нулю и, значит, искомый угол между прямыми DA1 и BD1 равен 90о. имеет координаты (-1, 1, 1). Скалярное произведение этих векторов равно нулю и, значит, искомый угол между прямыми DA1 и BD1 равен 90о.
Ответ. 90о.
1.3. Первое решение. Обозначим D и F1 соответственносередины ребер AC и A1B1.
Прямые DC1 и DF1 будут соответственно параллельны прямым AD1 и CE1. Следовательно, угол между прямыми AD1 и CE1 будет равен углу C1DF1. Треугольник C1DF1 равнобедренный, DC1 = DF1 = Второе решение. Введем систему координат, считая началом координат точку A, как показано на рисунке. Точка C имеет координаты
Ответ. 0,7.
Тренировочная работа 1. Угол между прямыми
1. В кубе A…D1 найдите косинус угла между прямыми AB и CA1.
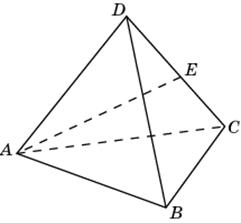
2. В правильном тетраэдре ABCD точка E – середина ребра CD. Найдитекосинус угла между прямыми BC и AE.
3. В правильной треугольной призме ABCA1B1C1, все ребра которой равны 1, найдите косинус угла между прямыми AB и CA1.
4. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точка E – середина ребра SD. Найдите тангенс угла между прямыми SB и AE.
5. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите косинус угла между прямыми AB и FE1.
6. В правильной шестиугольной призме A…F1, все ребра которой равны 1, найдите косинус угла между прямыми AB1 и BC1.
7. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AE.
8. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите косинус угла между прямыми SB и AD.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



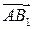 имеет координаты (1, 0, 1). Вектор
имеет координаты (1, 0, 1). Вектор 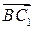 имеет координаты (0, 1, 1). Воспользуемся формулой нахождения косинуса угла
имеет координаты (0, 1, 1). Воспользуемся формулой нахождения косинуса угла  между векторами
между векторами  и, значит, угол
и, значит, угол 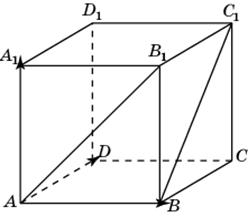
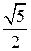 , C1F1 =
, C1F1 =  . Используя теорему косинусов, получаем
. Используя теорему косинусов, получаем 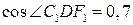 .
.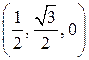 , точка D1 имеет координаты
, точка D1 имеет координаты 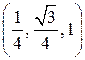 , точка E1 имеет координаты
, точка E1 имеет координаты 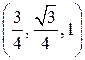 . Вектор
. Вектор  имеет координаты
имеет координаты 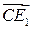 имеет координаты
имеет координаты 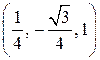 . Косинус угла между прямыми AD1 и CE1 равен косинусу угла между векторами
. Косинус угла между прямыми AD1 и CE1 равен косинусу угла между векторами 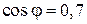 .
.