
|
|
РЕШЕНИЕ СИСТЕМ УРАВНЕНИЙ И НЕРАВЕНСТВСоставление алгоритма решения систем уравнений методом подстановки. · Из любого уравнения выразить x или y (например: y из 1 уравнения). · В другое уравнение вместо выраженной переменной (y) подставить полученное буквенное выражение . · Получилось уравнение с одной переменной (x). Решив его, найти значение переменной (x). · Подставить найденное значение переменной (x) в выражение, определённое на первом шаге (например: y). Вычислить значение другой переменной (y). VI. Решение систем способом подстановки: № 1. Решить систему Решение: y = 1/2 +1 = 1,5 . Ответ: ( 1/2; 1,5 ) . № 2. Решить систему Решение: Ответ: (21; 34).
Метод сложения Ввести решение систем методом алгебраического решения с помощью решения системы уравнения:
РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ Рациональные уравнения
Термин «рациональное уравнение» мы ввели выше в § 7. Сначала напомним, что такое рациональное выражение. Это — алгебраическое выражение, составленное из чисел и переменной х с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем. Если r(х) — рациональное выражение, то уравнение r(х) = 0 называют рациональным уравнением. Впрочем, на практике удобнее пользоваться несколько более широким толкованием термина «рациональное уравнение»: это уравнение вида h(x) = q(x), где h(x) и q(x) — рациональные выражения. До сих пор мы могли решить не любое рациональное уравнение, а только такое, которое в результате различных преобразований и рассуждений сводилось к линейному уравнению. Теперь наши возможности значительно больше: мы сумеем решить рациональное уравнение, которое сводится не только к линейно- Напомним, как мы решали рациональные уравнения раньше, и попробуем сформулировать алгоритм решения. Пример 1. Решить уравнение
Решение. Перепишем уравнение в виде
При этом, как обычно, мы пользуемся тем, что равенства А = В и А - В = 0 выражают одну и ту же зависимость между А и В. Это и позволило нам перенести член Выполним преобразования левой части уравнения. Имеем
1) числитель дроби равен нулю (а = 0); 2) знаменатель дроби отличен от нуля
Осталось проверить выполнение второго указанного выше условия. Соотношение Ответ: 2; 0,6. Если среди корней числителя окажется число, при котором знаменатель дроби обращается в нуль, то такое число корнем уравнения быть не может, его называют посторонним корнем и в ответ не включают. Опираясь на решенный пример, сформулируем следующий алгоритм.
1) Преобразуем уравнение к виду
2) Выполним преобразования левой части этого уравнения:
(одновременно изменили знаки в числителе и знаменателе
3) Решим уравнение х2 - 6x + 8 = 0. Находим
4) Для найденных значений проверим выполнение условия 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

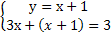 ,
,  , 4х = 2 , х = 1/2.
, 4х = 2 , х = 1/2.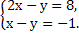

 ,
,  ,
,  , y = 34, x = 21.
, y = 34, x = 21.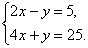
 , для этого надо сложить два уравнения системы:
, для этого надо сложить два уравнения системы: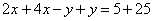 ;
; 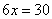 ;
; 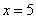 .
.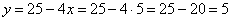 .
.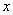 или при переменной
или при переменной 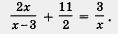
 в левую часть уравнения с противоположным знаком.
в левую часть уравнения с противоположным знаком.
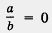 тогда, и только тогда, когда одновременно выполняются два соотношения:
тогда, и только тогда, когда одновременно выполняются два соотношения: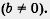 ).
). 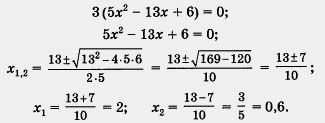
 . Значения х1 = 2 и х2 = 0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения.
. Значения х1 = 2 и х2 = 0,6 указанным соотношениям удовлетворяют и потому служат корнями уравнения (1), а вместе с тем и корнями заданного уравнения.

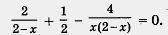

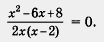
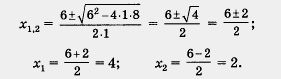
 . Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень.
. Число 4 этому условию удовлетворяет, а число 2 — нет. Значит, 4 — корень заданного уравнения, а 2 — посторонний корень.