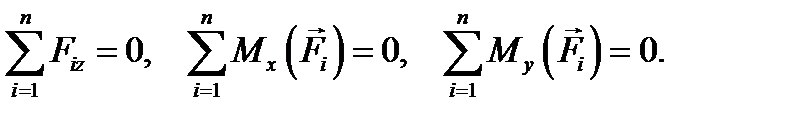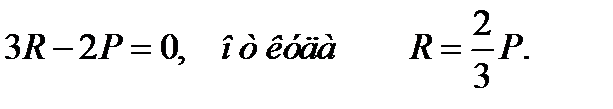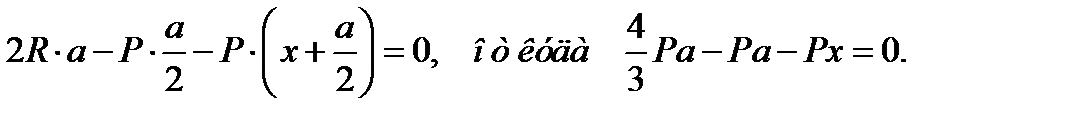|
|
ПРИМЕРЫ РЕШЕНИЯ ОЛИМПИАДНЫХ ЗАДАЧЗАДАЧА 11
Решение Найдем проекции на координатные оси главного вектора:
Модуль главного вектора также равен нулю (3-й, 4-й и 5-й ответы неверны). Найдем проекции на координатные оси главного момента:
Модуль главного момента не равен нулю (6-й ответ неверен). При этом результирующая пара не дает момента относительно оси х (1-й ответ неверен). Ответ:Верным является второй ответ. ЗАДАЧА 12
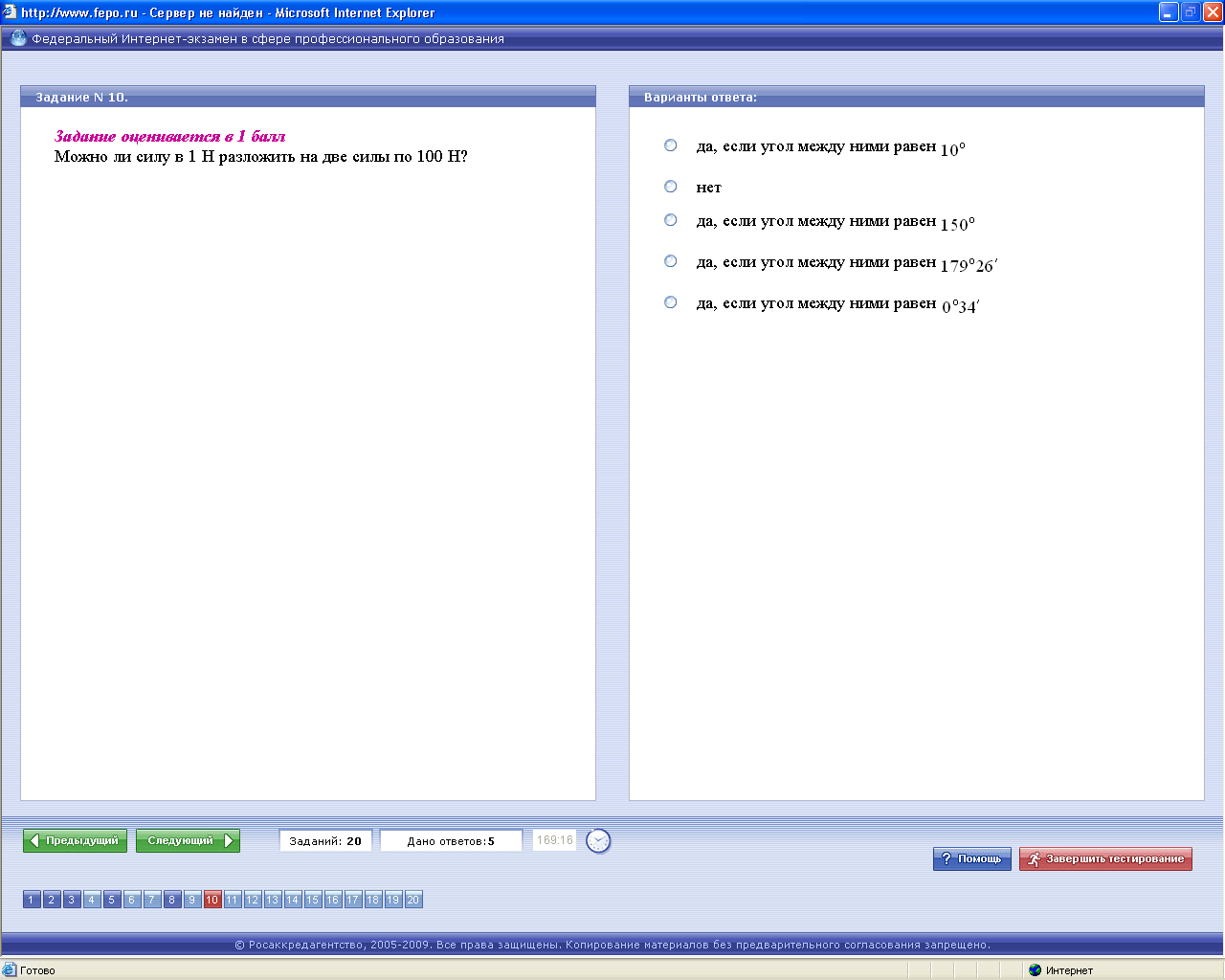
Решение Как известно, система из двух сил, приложенных в одной точке, имеет равнодействующую, равную их векторной сумме, и приложенную в той же точке. Модуль этой равнодействующей можно определить с помощью теоремы косинусов по формуле
где φ – угол меду исходными векторами. Пусть, некая сила, модуль которой равен R,является равнодействующей двух приложенных в одной точке сил, модули которых равны Р. Тогда
Отсюда следует, что
Ответ:Верным является четвертый ответ. ЗАДАЧА 13
Решение
Оставшаяся в рассмотрении часть конструкции (так же как и вся конструкция в целом) должна находиться в равновесии.
Как известно, условие равновесия произвольной плоской системы сил включает в себя три уравнения:
Искомую силу N2 легко найти из второго уравнения этой системы:
Ответ:Верным является второй ответ.
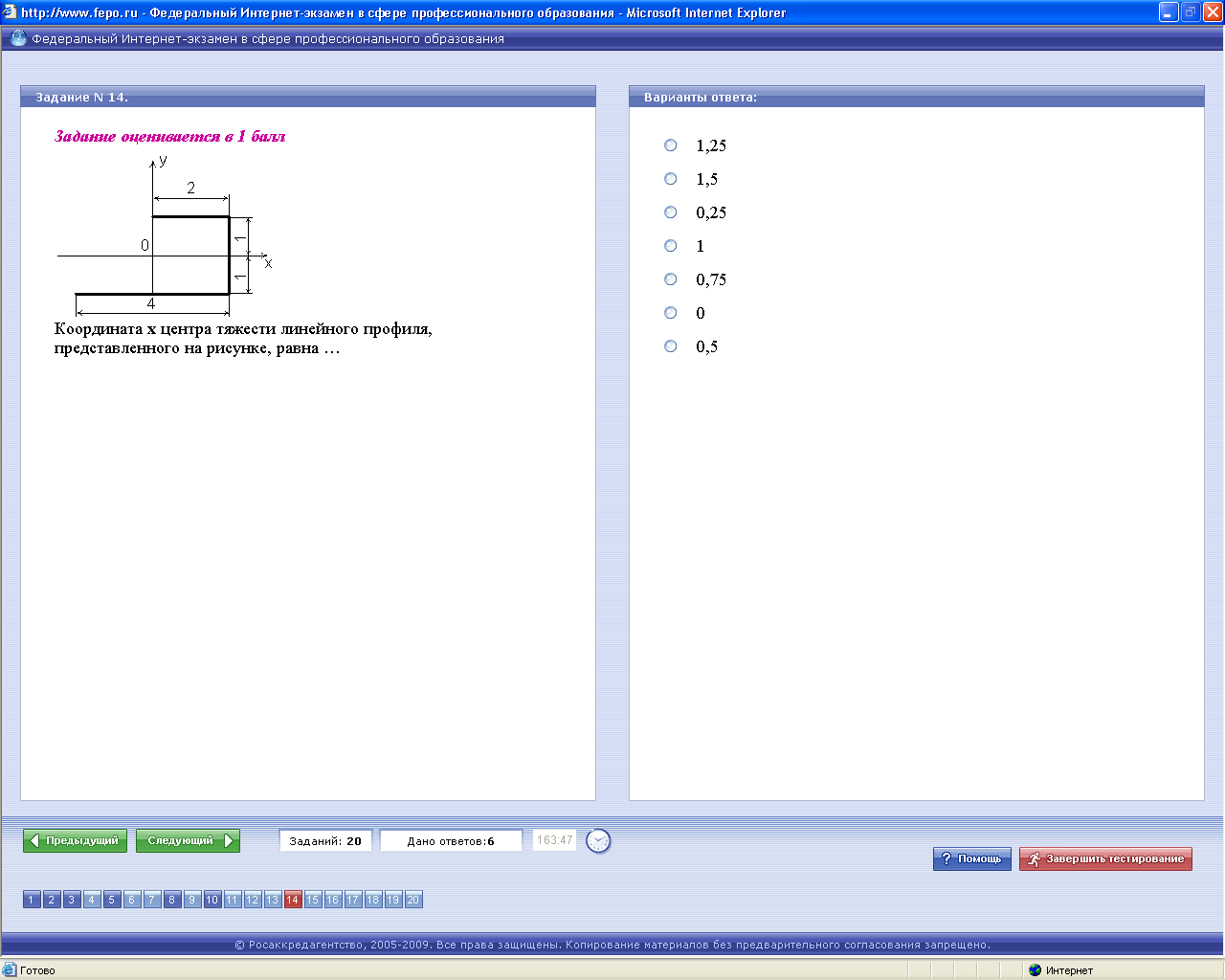
ЗАДАЧА 14
Решение
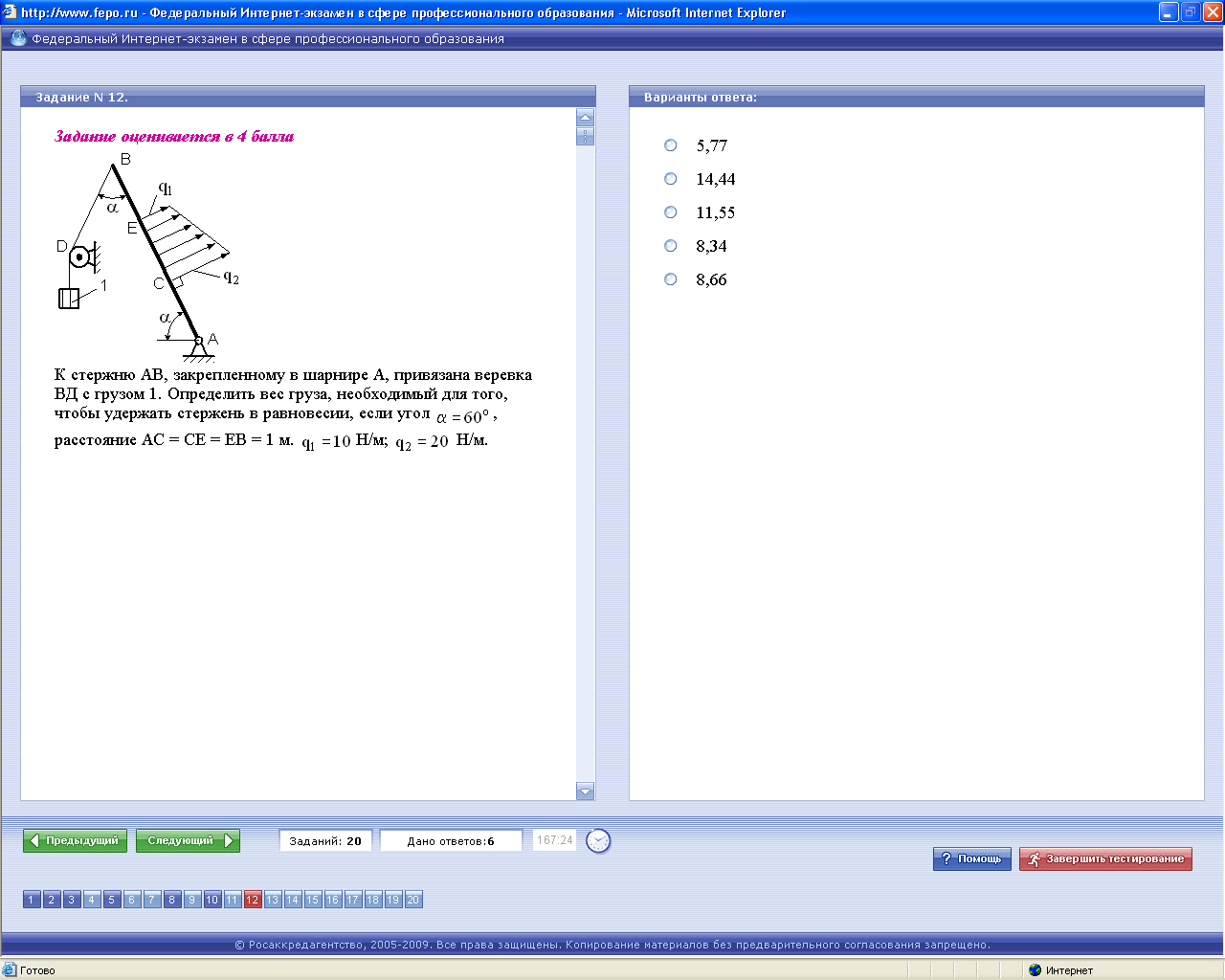
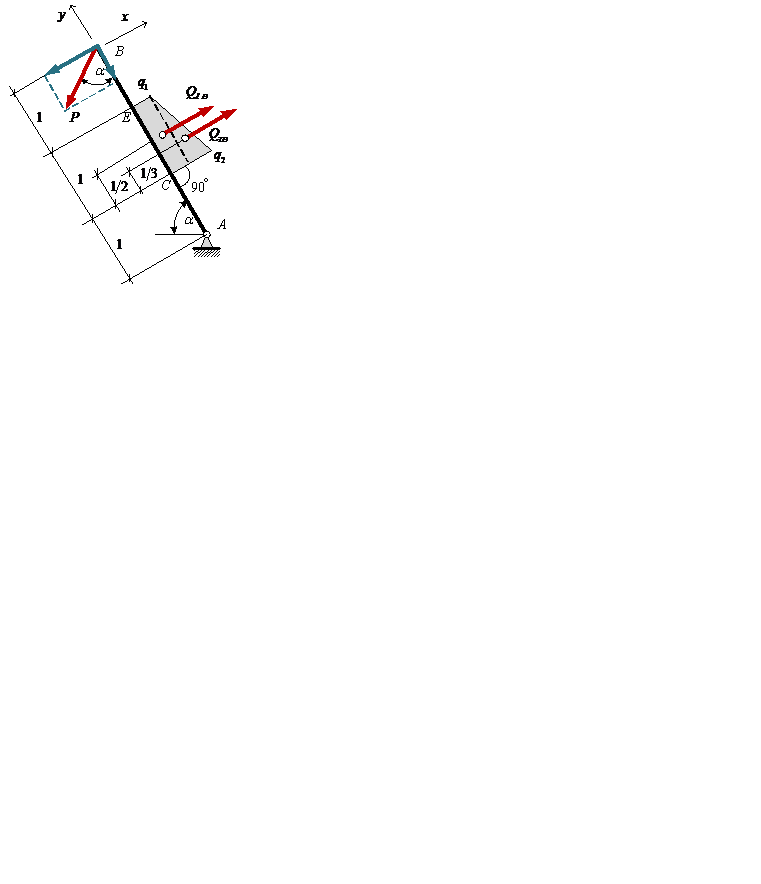
Для определения веса груза Р составим уравнение равновесия в виде ∑MА(F)=0:
где
Учитывая, что α = 600, получим следующее уравнение:
решая которое, получим:
Ответ:Верным является четвертый ответ. ЗАДАЧА 15
Решение Равнодействующая и уравновешивающая силы образуют уравновешенную систему сил, поэтому по аксиоме о равновесии двух сил они равны по модулю, действуют вдоль одной линии действия и направлены в противоположные стороны. Ответ:Верными являются четвертое, пятое и шестое суждения. ЗАДАЧА 16
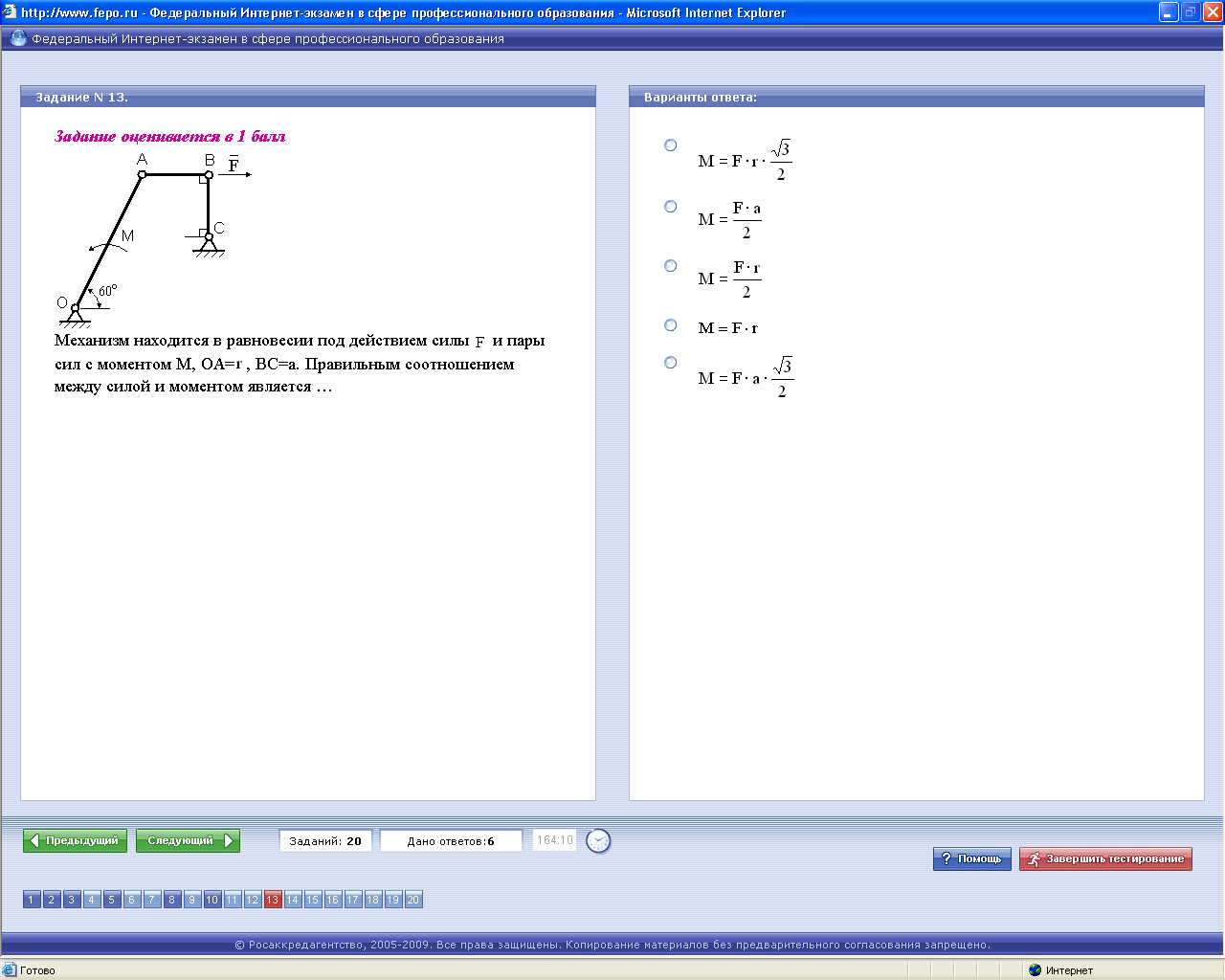
Решение Разобьем механизм на три диска: 1, 2 и 3, между которыми возникают силы взаимодействия в шарнирах А и В. Эти силы взаимодействия Линия действия реакции Rc пройдет по линии соединяющей шарниры С и В, так как тело ВС представляет собой стержень с шарнирами по концам. В этом случае, из уравнения Из аксиомы о равновесии двух сил и аксиомы о взаимодействии двух тел следует, что силы взаимодействия в шарнирах А и В равны по модулю, то есть Так как механизм находится в равновесии, для определения соотношения между моментом и силой составим для первого диска уравнение равновесия вида ∑Mо(F)=0:
Из этого уравнения видно, что для равновесия необходимо следующее соотношение между моментом и силой: М = F r Ответ:Верным является первый ответ. ЗАДАЧА 17
Решение Координату xС центра тяжести ломаного стержня определим по формуле:
Ответ:Верным является пятый ответ. ЗАДАЧА 18
Решение Рассмотрим цилиндры 1 и 2 по отдельности.
Силы взаимодействия между цилиндрами, обозначенные на рисунках 1 и 2 как N и N’, наклонены к вертикали под неизвестным углом γ. Каждый из цилиндров, как это видно из рисунков, загружен плоской сходящейся системой сил. Для равновесия каждой из этих систем, как известно, должны выполняться два уравнения:
Таким образом, для решения задачи необходимо сформировать систему из четырех уравнений равновесия:
Третье из этих уравнений выполняется тождественно в силу симметрии системы сил, приложенной ко второму цилиндру. В оставшиеся три уравнения входят три неизвестные величины: силы N и P и угол γ. Сформируем уравнения (1), (2) и (4):
Удваивая слагаемые уравнения (2) и складывая уравнение (2) с уравнением (4), получим: откуда следует, что Подставляя полученное выражение в уравнения (1) и (2), получим следующую систему:
Возводя эти уравнения в квадрат, и складывая их, получим:
откуда Из уравнения (4) выразим неизвестный угол:
Учитывая, что Найдем неизвестный угол, который будет равен Ответ:Верным является пятый ответ. ЗАДАЧА 19
Решение Примем, что все три реакции равны по модулю. Вес каждой из плит обозначим Р. Модули реакций (неизвестные) обозначим R. Условие равновесия пространственной системы параллельных сил включает в себя три следующих уравнения:
Если выбрать систему координат, поместив ее начало в точку А, как это показано на рисунке, то третье уравнение в силу симметрии системы обратится в тождество. Из первого уравнения получим:
Учитывая, что координаты «y» центра тяжести первой (нижней) плиты равна y1 = а/2, а второй – y2 = x+а/2, сформируем второе уравнение системы:
Выражая из уравнения неизвестную величину х, получим, что х = а/3. Ответ:Верным является третий ответ. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|



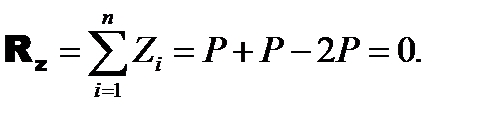
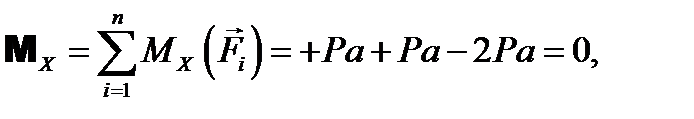
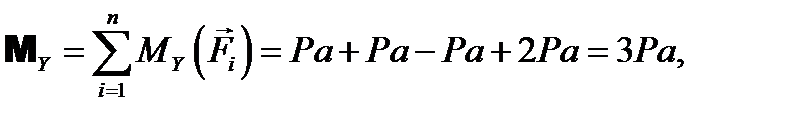
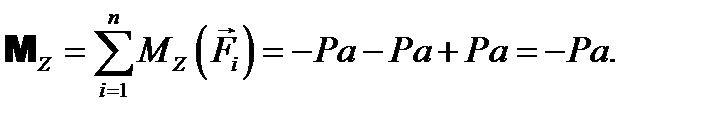
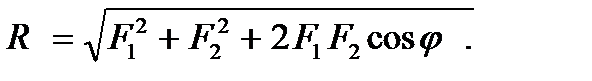

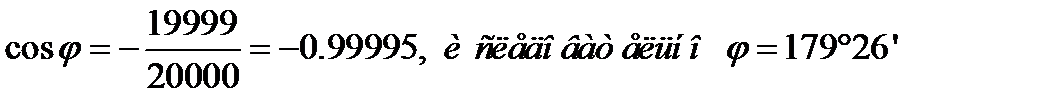
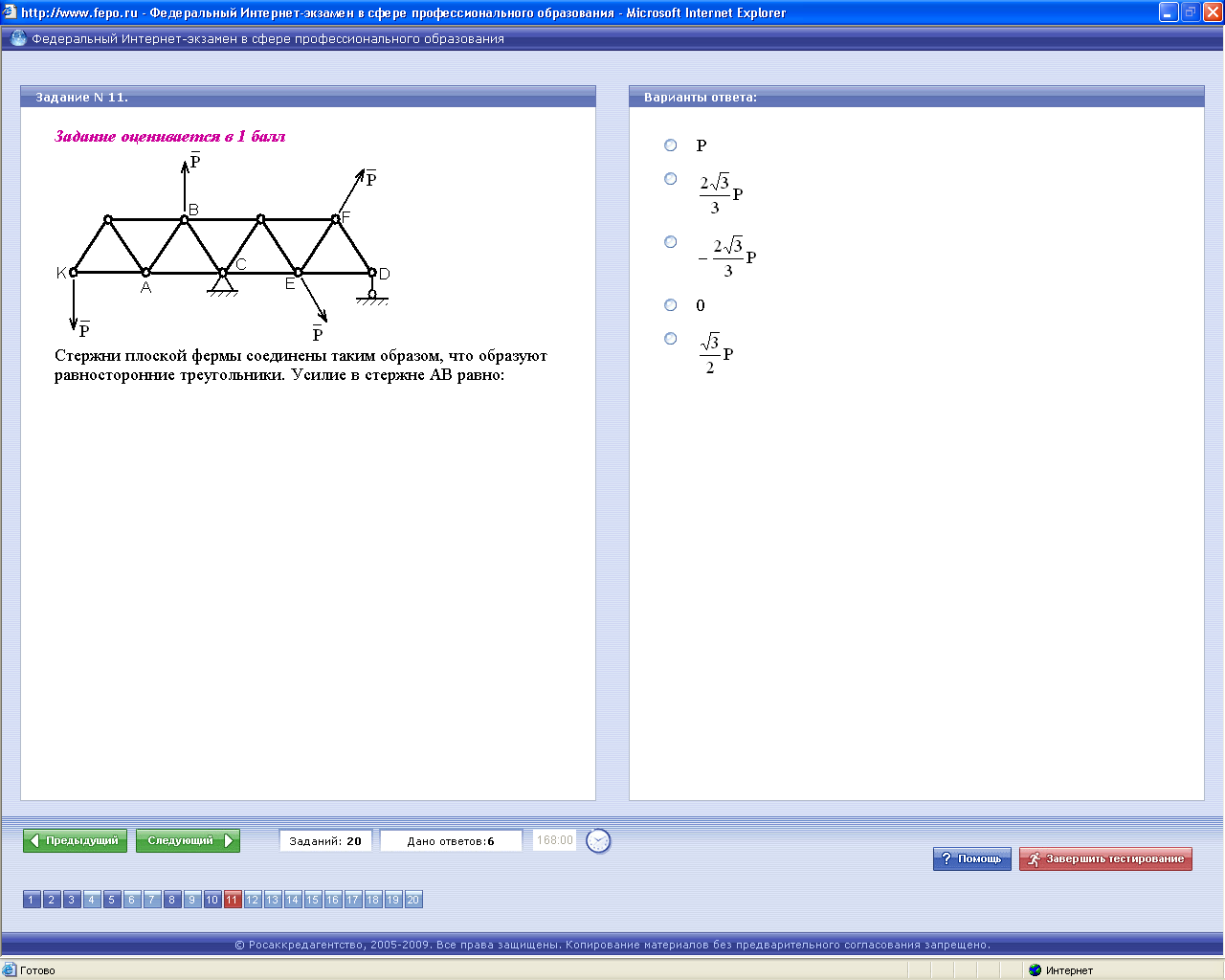
 Рассечем три стержня фермы так, как показано на рисунке. Отбросим правую часть фермы, заменив ее действие неизвестными силами, возникающими в стержнях. Будем считать, что все три стержня растянуты.
Рассечем три стержня фермы так, как показано на рисунке. Отбросим правую часть фермы, заменив ее действие неизвестными силами, возникающими в стержнях. Будем считать, что все три стержня растянуты.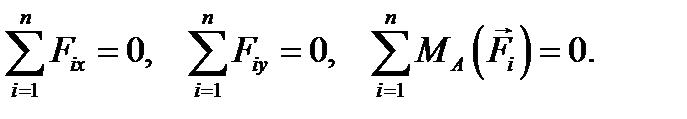
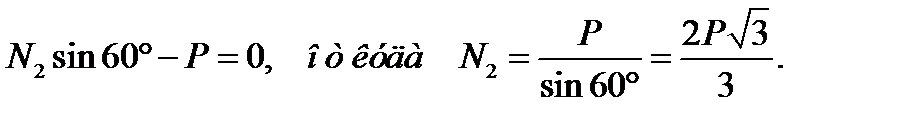

 =0,
=0, – равнодействующие прямоугольной и треугольной составляющих распределенной нагрузки:
– равнодействующие прямоугольной и треугольной составляющих распределенной нагрузки: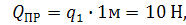
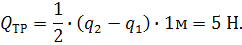

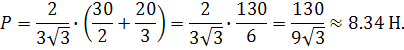
 направлены вдоль диска АВ, поскольку он представляет собой стержень с шарнирами по концам (здесь
направлены вдоль диска АВ, поскольку он представляет собой стержень с шарнирами по концам (здесь 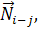 означает силу, с которой диск с номером i действует на диск с номером j).
означает силу, с которой диск с номером i действует на диск с номером j). , составленного для 3-го диска следует, что
, составленного для 3-го диска следует, что 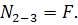
 Отсюда следует, что сила
Отсюда следует, что сила  по модулю тоже будет равна F.
по модулю тоже будет равна F.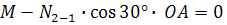 или
или 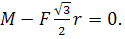
 .
.



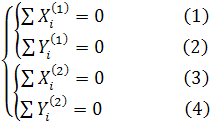
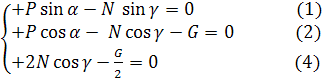

 .
.
 ,
, .
. .
. получим значение
получим значение  .
.