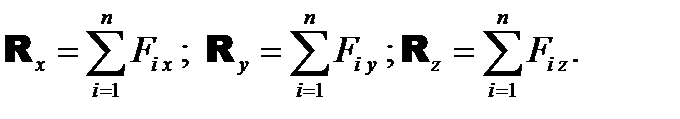|
|
Шарнирно-неподвижная опораТЕОРЕТИЧЕСКИЕ ПОЛОЖЕНИЯ СИЛЫ И СИСТЕМЫ СИЛ Совокупность нескольких сил Если одну систему сил, действующую на свободное твердое тело, можно заменить другой системой сил так, что при этом кинематическое состояние тела не изменится, то эти системы сил называют эквивалентными друг другу. Для обозначения эквивалентности систем сил используются символ Одна сила, эквивалентная некоторой системе сил, называется ее равнодействующей. Она обозначается символом Система сил, не выводящая из равновесия свободное твердое тело, называется уравновешенной системой, или эквивалентной нулю. Силу можно переносить вдоль линии действия в любую точку данного тела,не меняя ее модуля и направления. Система из двух сил, приложенных в одной точке, имеет равнодействующую, равную их векторной сумме и приложенную в той же точке. Модуль и направление равнодействующей двух сил, приложенных в одной точке, можно определить, используя формулы тригонометрии для треугольников. По теореме косинусов модуль равнодействующей равен:
По теореме синусов:
Отсюда можно определить направление равнодействующей.
СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Ограничения, наложенные на перемещения (скорости) точек механической системы, называются связями. Связи всегда осуществляются какими-либо материальными телами. Реакцией связи называется сила, с которой связь действует на тело. Силы, не являющиеся реакциями связей, называют активными силами или нагрузками. Определение реакций, наложенных на механическую систему связей при ее равновесии, составляет содержание большинства решаемых в статике задач. Изучение равновесия несвободных тел основано на принципе освобождаемости от связей: Всякое несвободное тело можно рассматривать как свободное, если мысленно отбросить связи, заменив их действие соответствующими реакциями связей. Реакция всегда направлена в сторону, противоположную той, куда тело, осуществляющее связь, не дает перемещаться данному телу.
РАЗНОВИДНОСТИ СВЯЗЕЙ Свободное опирание Гладкая поверхность (поверхность без трения) позволяет взаимодействующему с ней телу свободно перемещаться по касательной плоскости в точке касания и не позволяет перемещаться в направлении нормали к этой плоскости. Реакция такой поверхности (сила При опирании углом или на угол реакция направлена по нормали к той поверхности, которая соприкасается с углом.
Реакция нити всегда направлена от тела вдоль нити (возникает только при натягивании нити).
Опорным стержнем принято называть невесомый стержень, прикрепляемый с двух сторон с помощью шаровых шарниров, которые допускают свободный поворот тел вокруг центра этого шарнира. Реакция такого стержня направлена по линии, которая проходит через центры опорных шарниров. Шарнирно-подвижная опора Такой тип опоры реализуется в виде опоры на катках. Для шарнирно-подвижной опоры известна точка приложения реакции (шарнир) и линия ее действия (она перпендикулярна опорной поверхности).
Шарнирно-неподвижная опора Для этой опоры известна точка приложения реакции (шарнир), а линия действия неизвестна, т.к. угол В этом случае силу
Жёсткая заделка препятствует любому поступательному перемещению тела, поэтому направление её реакции заранее определить нельзя и сначала определяют её составляющие Кроме того, жёсткая заделка препятствует повороту телу, поэтому, кроме силовой реакции, на тело действует ещё момент заделки ПРОЕКЦИИ СИЛЫ Проекцией вектора на ось называется скалярная величина равная произведению модуля вектора на косинус угла между направлением силы и положительным направлением оси. Рассмотрим некоторые частные случаи проектирования вектора на ось: Проекцией вектора на плоскость называется вектор, заключенный между проекциями начала и конца вектора на эту плоскость.
ГЛАВНЫЙ ВЕКТОР СИСТЕМЫ СИЛ Главный вектор системы сил равен векторной сумме всех сил системы:
Модуль главного вектора равен
где
РАВНОДЕЙСТВУЮЩАЯ СХОДЯЩЕЙСЯ СИСТЕМЫ СИЛ Сходящейся системой сил называются совокупность сил, линии действия которых пересекаются в одной точке. Система сходящихся сил имеет равнодействующую, приложенную в точке пересечения линий действия сил, которая геометрически равна главному вектору этой системы сил.
ТЕОРЕМА О ТРЕХ СИЛАХ При решении задач удобно пользоваться теоремой: 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется системой сил.
называется системой сил. .
. .
.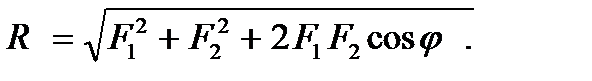
 .
. ) направлена по общей нормали.
) направлена по общей нормали. Гибкая нить (трос, канат, цепь)
Гибкая нить (трос, канат, цепь)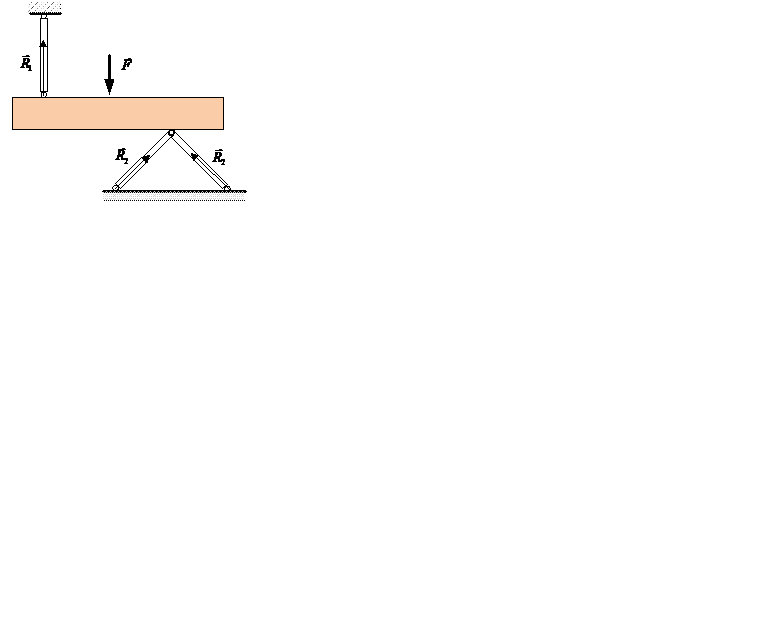 Опорный стержень
Опорный стержень может быть любым.
может быть любым. неизвестного направления удобно разложить на две неизвестные силы
неизвестного направления удобно разложить на две неизвестные силы  и
и  , направленные по координатным осям.
, направленные по координатным осям. Жесткая заделка
Жесткая заделка и
и  .
. , уравновешивающий стремление нагрузок повернуть тело в заделке.
, уравновешивающий стремление нагрузок повернуть тело в заделке.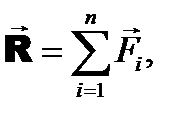
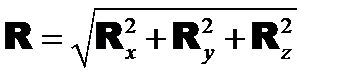
 - проекции главного вектора на координатные оси:
- проекции главного вектора на координатные оси: