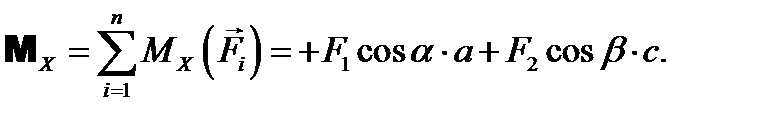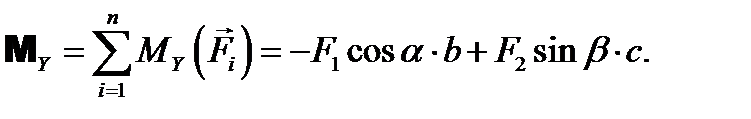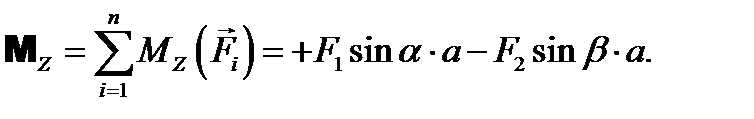|
|
Момент равнодействующей системы сил относительно некоторой оси равен алгебраической сумме моментов всех сил системы относительно этой оси.ГЛАВНЫЕ МОМЕНТЫ СИЛ Главным моментом
Модуль главного момента равен
где
ПАРА СИЛ, МОМЕНТ ПАРЫ
Моментом пары
УРАВНЕНИЯ РАВНОВЕСИЯ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ. Условием равновесия произвольной пространственной системы сил является равенство нулю главного вектора и главного момента. Для этого необходимо, чтобы суммы проекций сил на каждую из координатных осей и суммы моментов сил относительно каждой из координатных осей были равны нулю:
Таким образом, в статике для произвольной пространственной системы сил в общем случае можно составить шесть уравнений равновесия.
ЧАСТНЫЕ СЛУЧАИ РАВНОВЕСИЯ СИСТЕМ СИЛ Сходящаяся система сил Если линии действия всех сил системы проходят через одну точку, то моменты сил относительно этой точки (или любой проходящей через нее оси) будут равны нулю. В этом случае уравнения моментов оказываются тождествами и остаются только уравнения проекций сил:
Система пар сил Если система сил состоит только из пар, для каждой из которых, как известно, векторная сумма сил равна нулю, то уравнения проекций сил оказываются тождествами. Тогда в системе остаются только уравнения для моментов пар:
Пространственная система параллельных сил Пусть линии действия всех сил параллельны друг другу. Направим ось z параллельно этим силам. В этом случае являются тождествами уравнения проекций сил на оси х и у, а также уравнения моментов сил относительно оси z. Тогда остаются три уравнения:
Эти уравнения называются уравнениями равновесия пространственной системы параллельных сил.
УРАВНЕНИЯ РАВНОВЕСИЯ ПЛОСКОЙ СИСТЕМЫ СИЛ Уравнения равновесия плоской системы сил в аналитической форме представлены только тремя уравнениями:
Это есть первая (основная) форма уравнений равновесия произвольной плоской системы сил. Можно показать, что этой системе уравнений равносильны еще две формы записей уравнений равновесия.
Это вторая форма уравнений равновесия плоской системы сил. (ось
Это третья форма уравнений равновесия плоской системы сил. (при этом точки А, В и С не должны лежать на одной прямой).
ЦЕНТР ТЯЖЕСТИ Положение центра тяжести некоторого объема, состоящего из нескольких частей, можно найти по формулам:
Координаты центра тяжести однородной тонкой пластины постоянной толщины определяются через площади отдельных ее частей
Центр тяжести однородного (имеющего одинаковую по длине площадь поперечного сечения и удельную плотность материала) длинного тонкого тела определяется через длины его участков
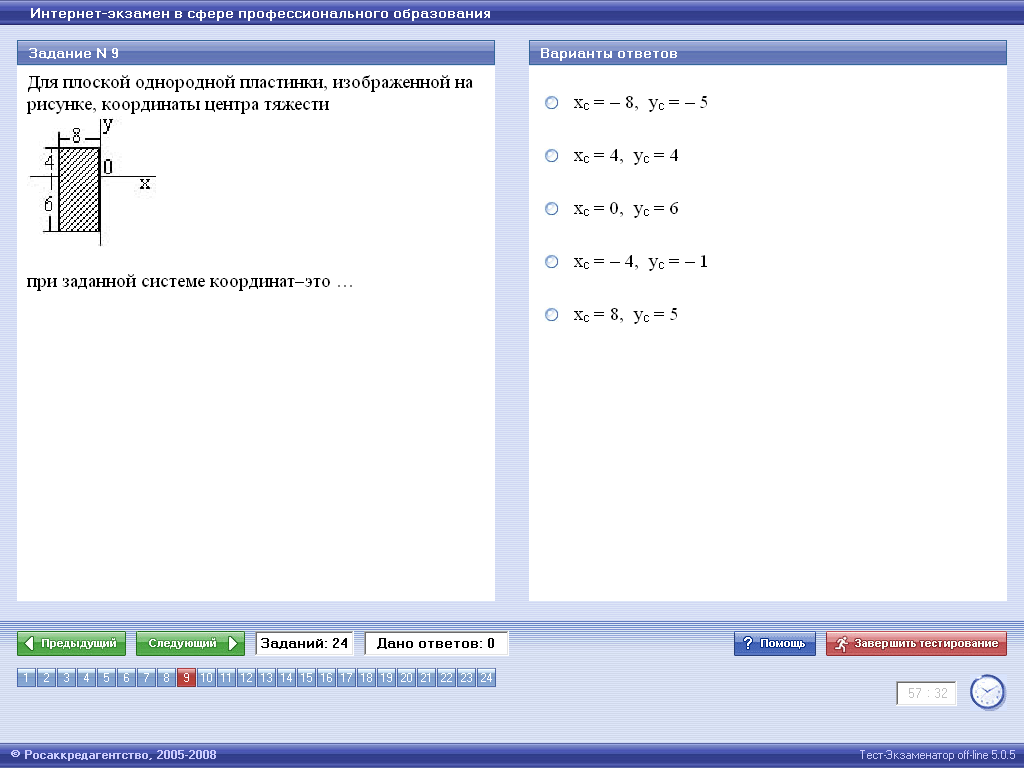
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ЗАДАЧА 1
Решение
Центр тяжести такой пластины находится на пересечении диагоналей прямоугольника, поэтому в показанной на рисунке системе координат координаты центра тяжести пластины будут равны Ответ:Верным является четвертый ответ.
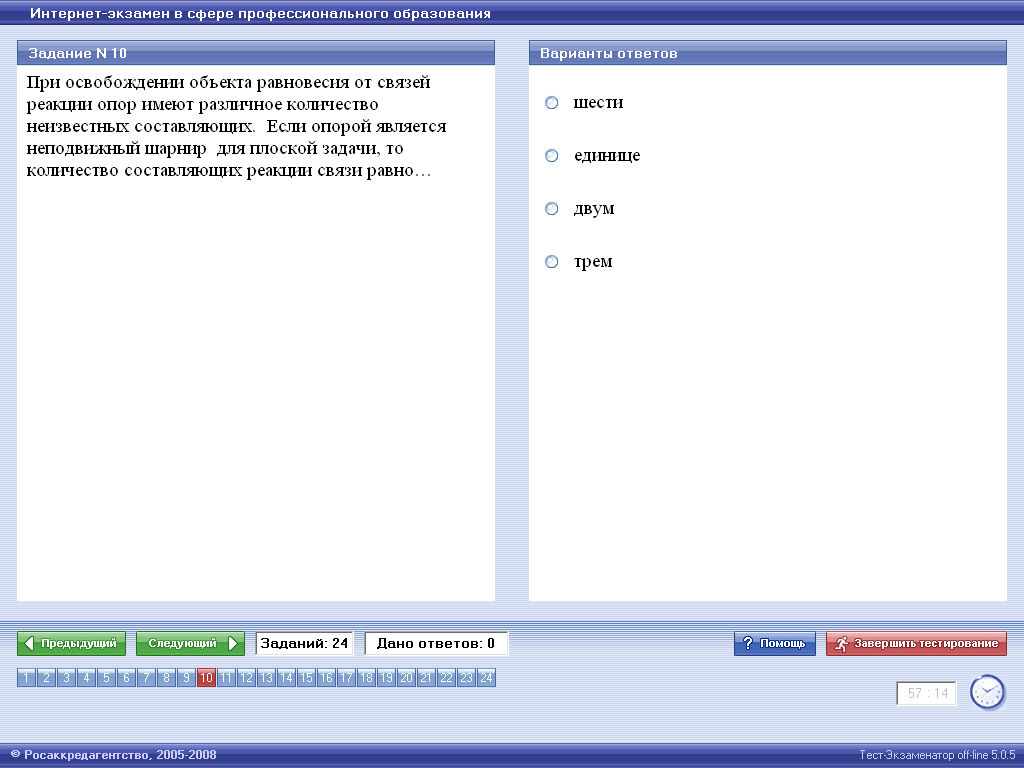
ЗАДАЧА 2
Ответ:Верным является третий ответ.
ЗАДАЧА 3
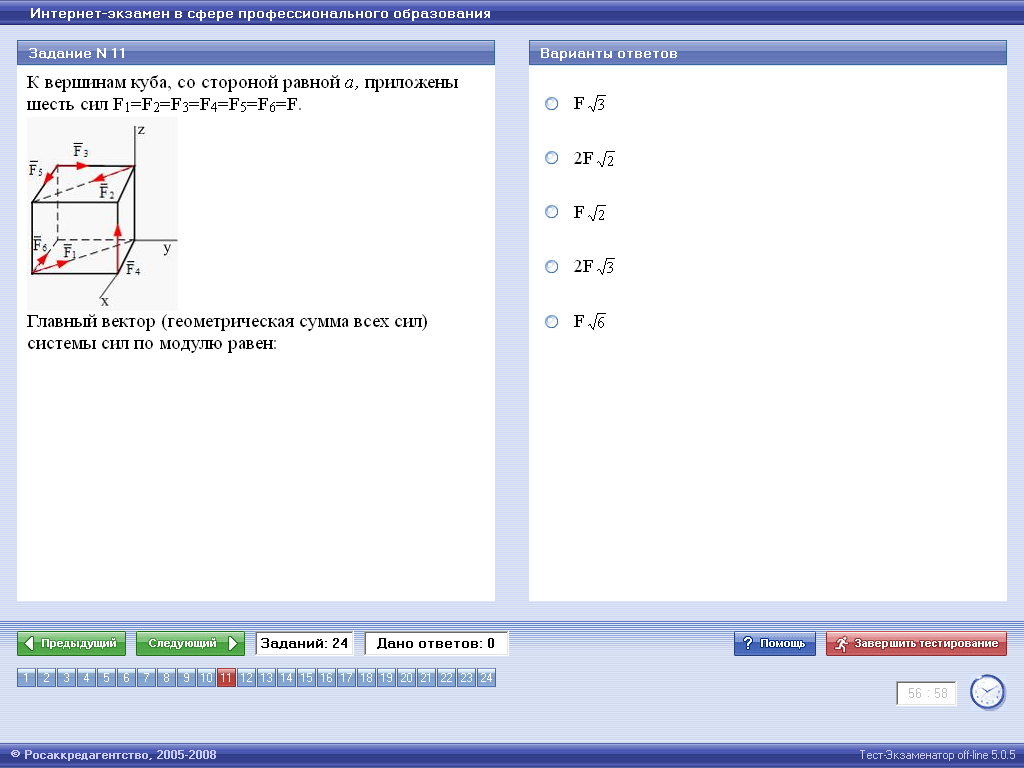
Решение Определяем проекции главного вектора на координатные оси:
Определяем модуль главного вектора:
Ответ:Верным является третий ответ. ЗАДАЧА 4
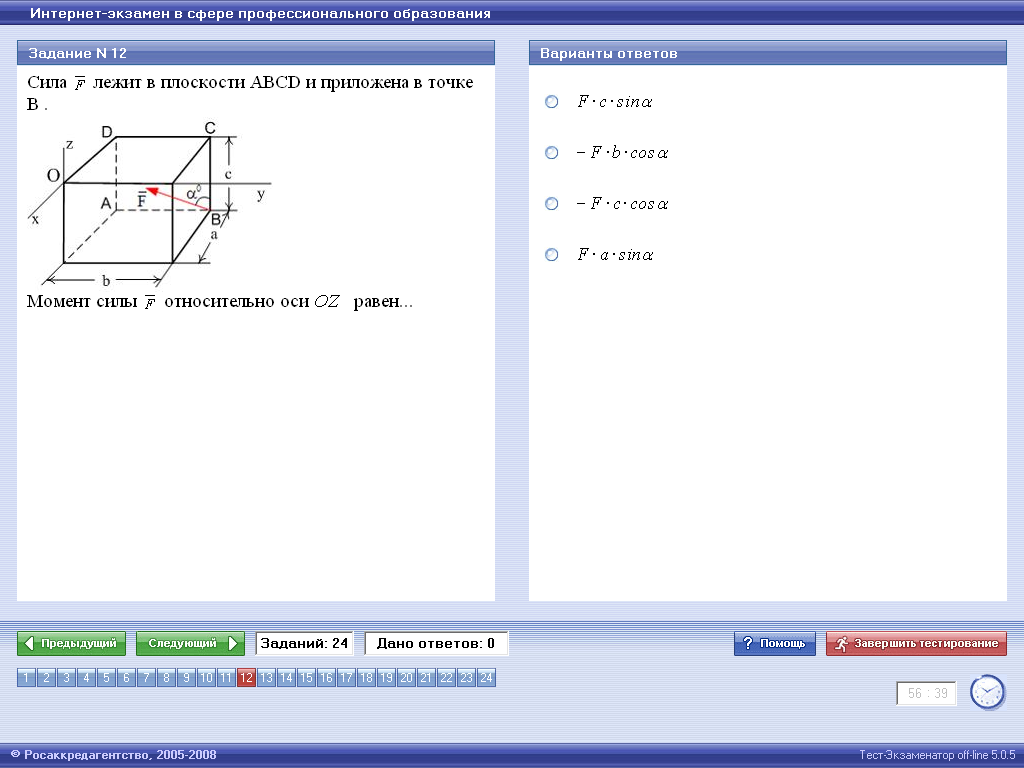
Решение Спроектируем силу на плоскость перпендикулярную указанной оси. Умножив модуль полученной проекции на плечо, получим модуль момента. Знак момента укажем, руководствуясь правилом правого винта.
Ответ:Верным является четвертый ответ. ЗАДАЧА 5
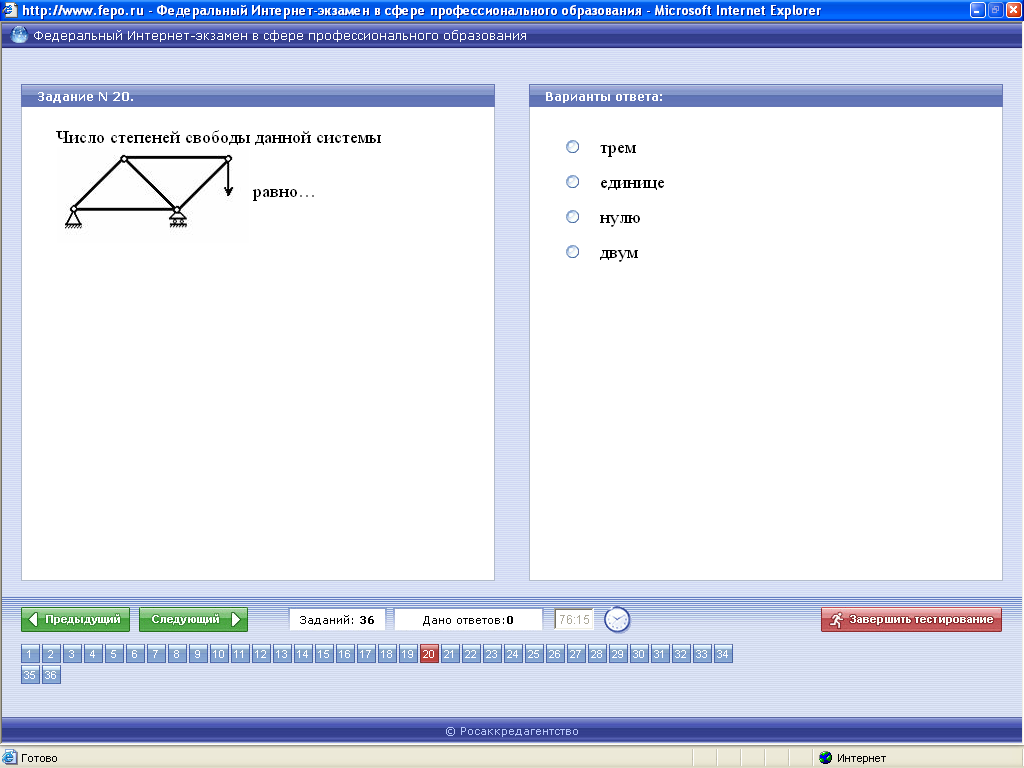
Решение Система, изображенная на рисунке, представляет собой геометрически неизменяемую ферму (диск), которая закреплена на опорах неподвижно. Любые формы движения для нее невозможны. Ответ:Верным является третий ответ.
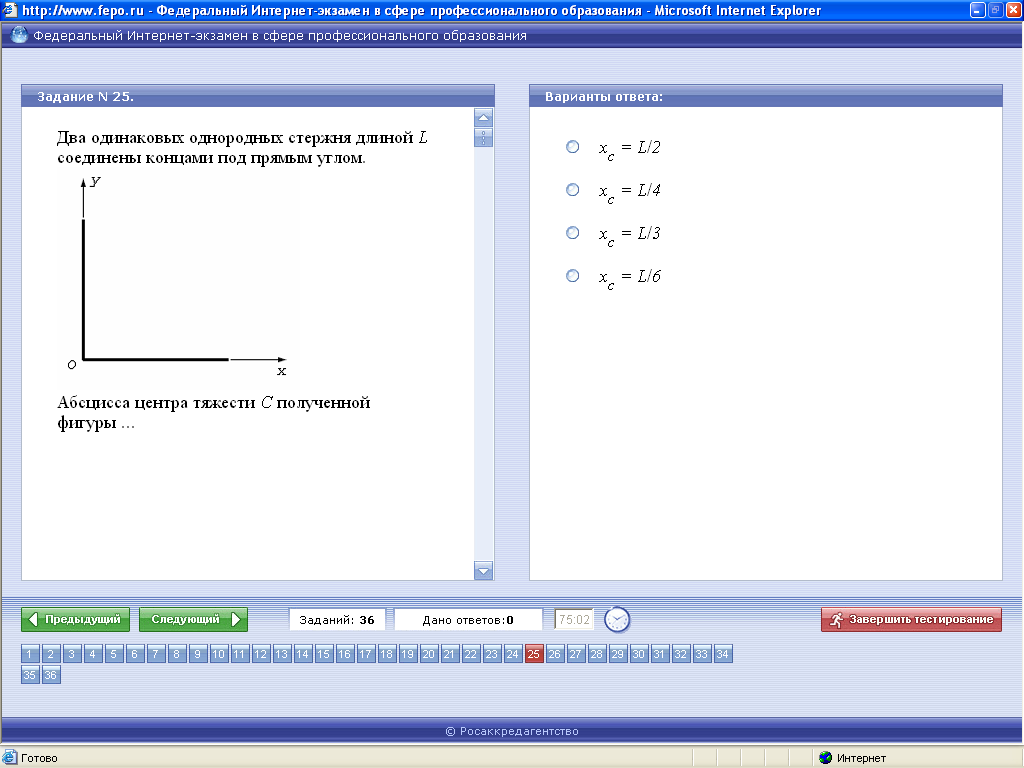
ЗАДАЧА 6
Решение Координату xС центра тяжести ломаного стержня определим по формуле:
Ответ:Верным является второй ответ.
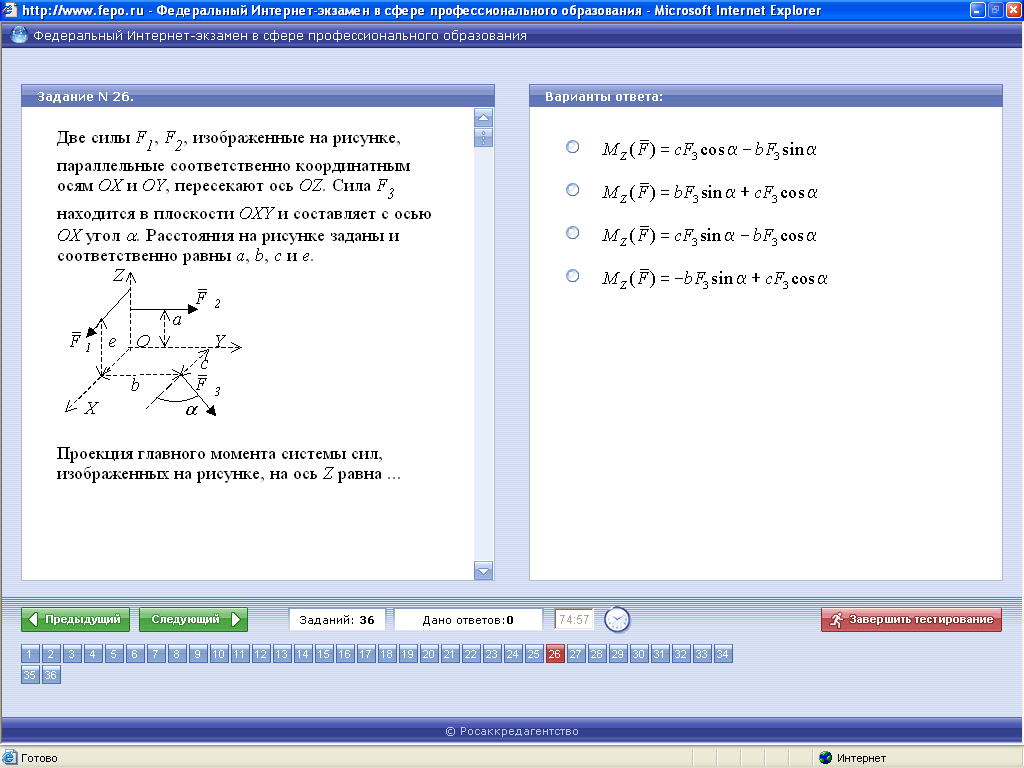
ЗАДАЧА 7
Решение Проекция главного момента системы сил на ось Z равна сумме моментов сил системы относительно этой оси. Моменты первой и второй сил равны нулю, поскольку их линии действия пересекают ось (равны нулю плечи). Для вычисления момента третьей силы можно использовать теорему Вариньона о моменте равнодействующей, разбив силу F3 на составляющие по осям x и y. Модули полученных составляющих умножим на соответствующие плечи, выбрав знаки произведений в соответствии с правилом правого винта: Ответ:Верным является третий ответ. ЗАДАЧА 8
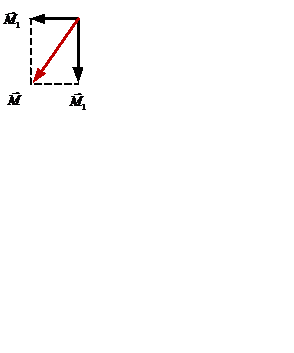
Решение Вектора моментов пар М1 и М2 направлены перпендикулярно плоскостям, в которых расположены пары, а направление моментов определяется правилом правого винта. Таким образом, результирующий вектор-момент геометрически совпадает с диагональю прямоугольника, стороны которого равны 3 Нм и 4 Нм. Модуль этого момента равен
Ответ:Верным является третий ответ.
ЗАДАЧА 9 Решение Вектор-момент перпендикулярен плоскости,в которой лежат точка О и вектора Ответ:Верным является второй ответ. ЗАДАЧА 10
Решение Проекции главного момента
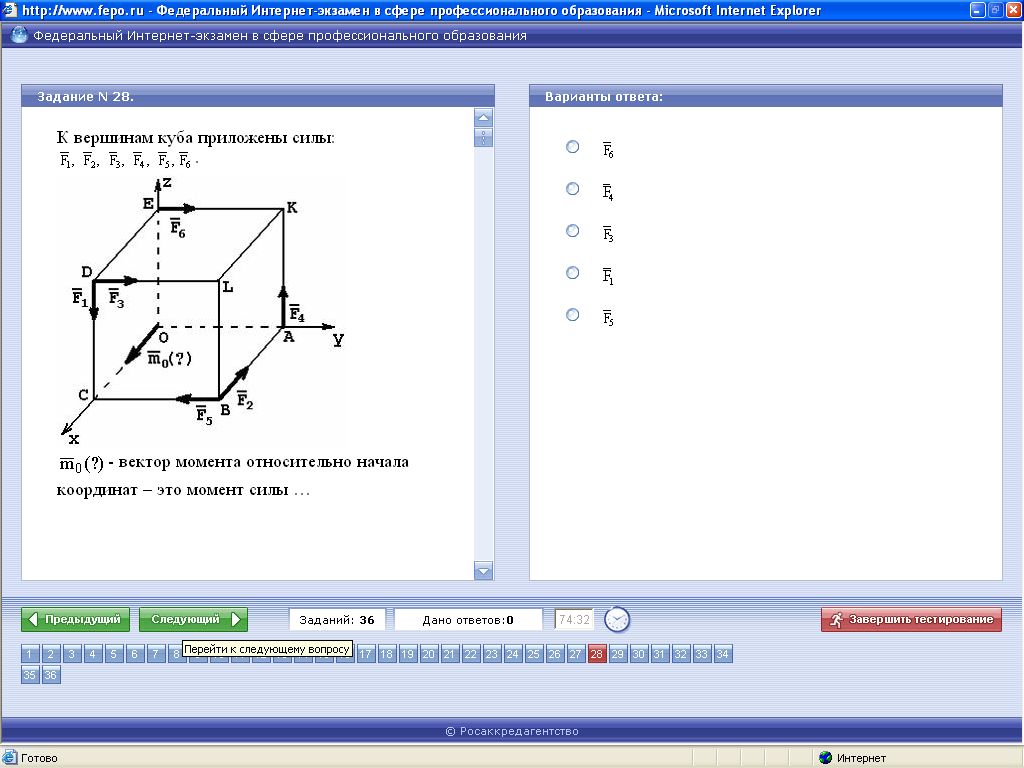
Чтобы вычислить момент силы относительно оси z, надо: 1. Спроектировать силу 2. Найти модуль момента, для чего следует перемножить модуль проекции силы 3. Выбрать знак в соответствии с правилом правого винта. Вычислим три проекции главного момента:
Ответ:Значение проекции главного момента на ось x приведено во второй строке ответа, на ось y – в третьей строке ответа, на ось z – в первой строке ответа. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 системы сил относительно некоторой точки О (данного центра) называется векторная сумма моментов всех сил системы относительно этой точки:
системы сил относительно некоторой точки О (данного центра) называется векторная сумма моментов всех сил системы относительно этой точки: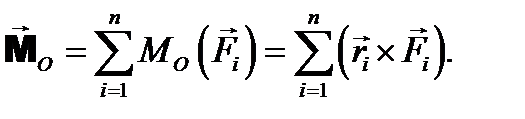
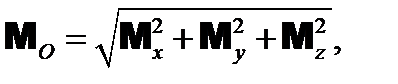
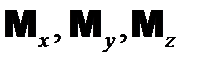 − проекции главного момента на координатные оси, проходящие через центр О:
− проекции главного момента на координатные оси, проходящие через центр О: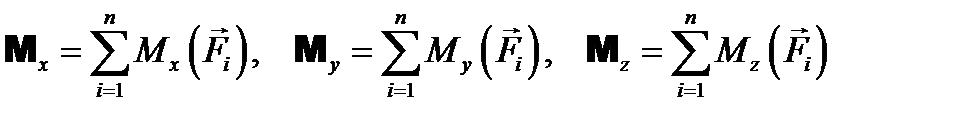
 Парой сил (или просто парой) называется система из двух равных по модулю, противоположно направленных параллельных сил.
Парой сил (или просто парой) называется система из двух равных по модулю, противоположно направленных параллельных сил. 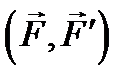 называется вектор
называется вектор  , направленный перпендикулярно плоскости действия пары в такую сторону, чтобы, глядя навстречу ему, видеть вращение, осуществляемое парой, происходящим против часовой стрелки(рис. 6.4), и равный по модулю произведению модуля одной из сил пары на плечо пары:
, направленный перпендикулярно плоскости действия пары в такую сторону, чтобы, глядя навстречу ему, видеть вращение, осуществляемое парой, происходящим против часовой стрелки(рис. 6.4), и равный по модулю произведению модуля одной из сил пары на плечо пары: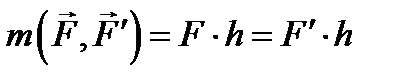
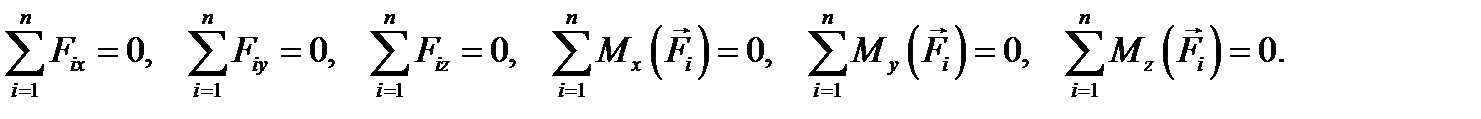
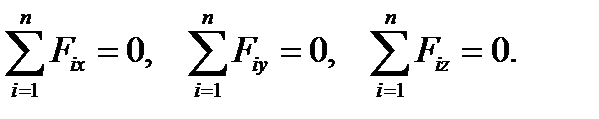
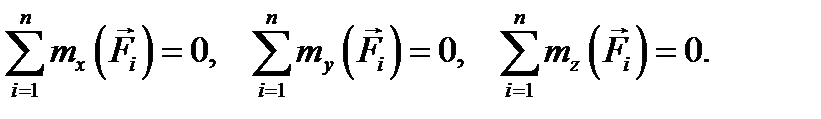
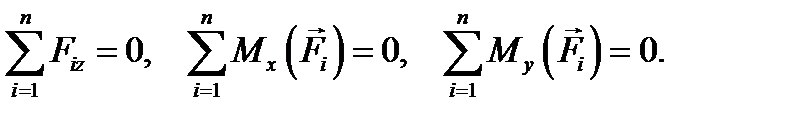
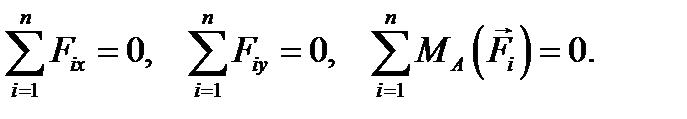
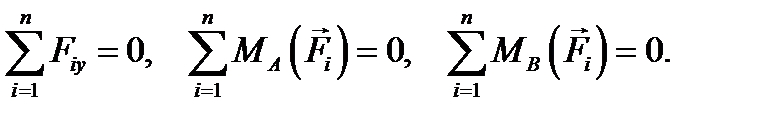
 не должна быть перпендикулярна линии АВ, иначе уравнения не будут независимы).
не должна быть перпендикулярна линии АВ, иначе уравнения не будут независимы).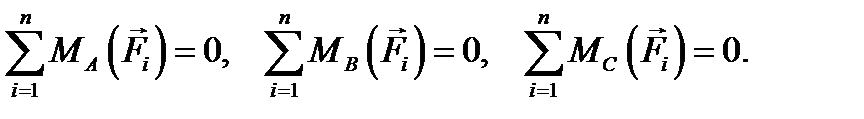
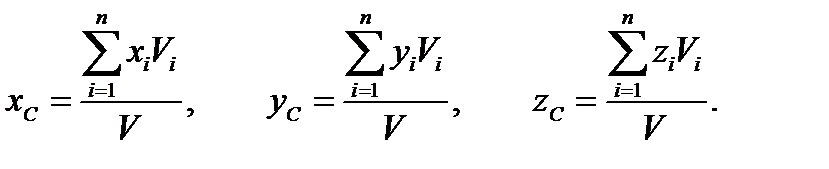
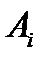 и общую площадь
и общую площадь 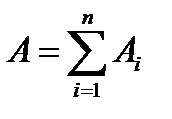 :
: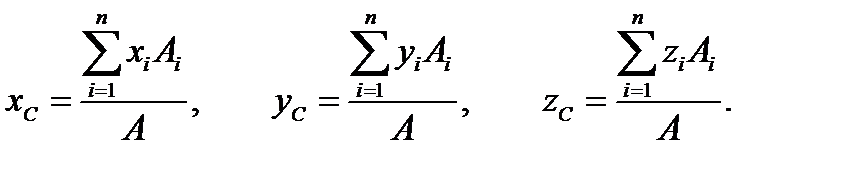
 и общую длину
и общую длину  :
: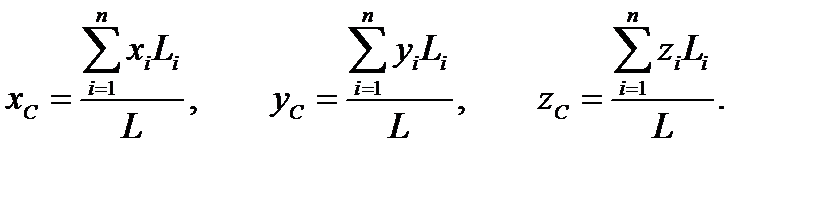

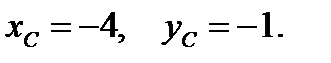

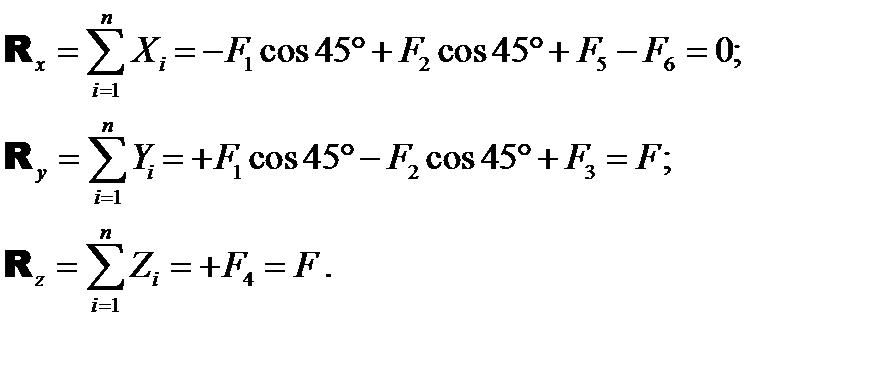
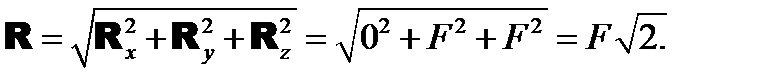

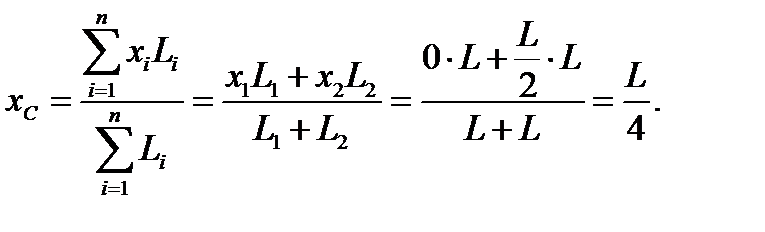
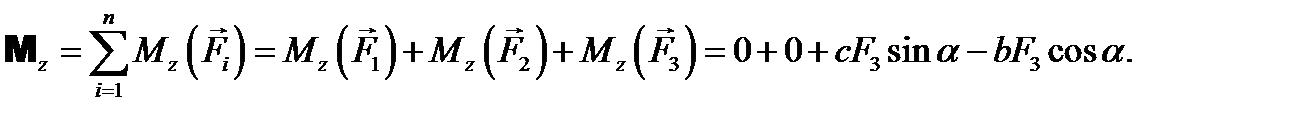

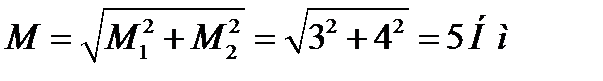
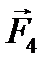 и
и 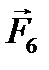 . Однако, в соответствии с правилом правого винта, направление вектор момента силы
. Однако, в соответствии с правилом правого винта, направление вектор момента силы 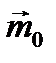 . Следовательно вектор-момент
. Следовательно вектор-момент 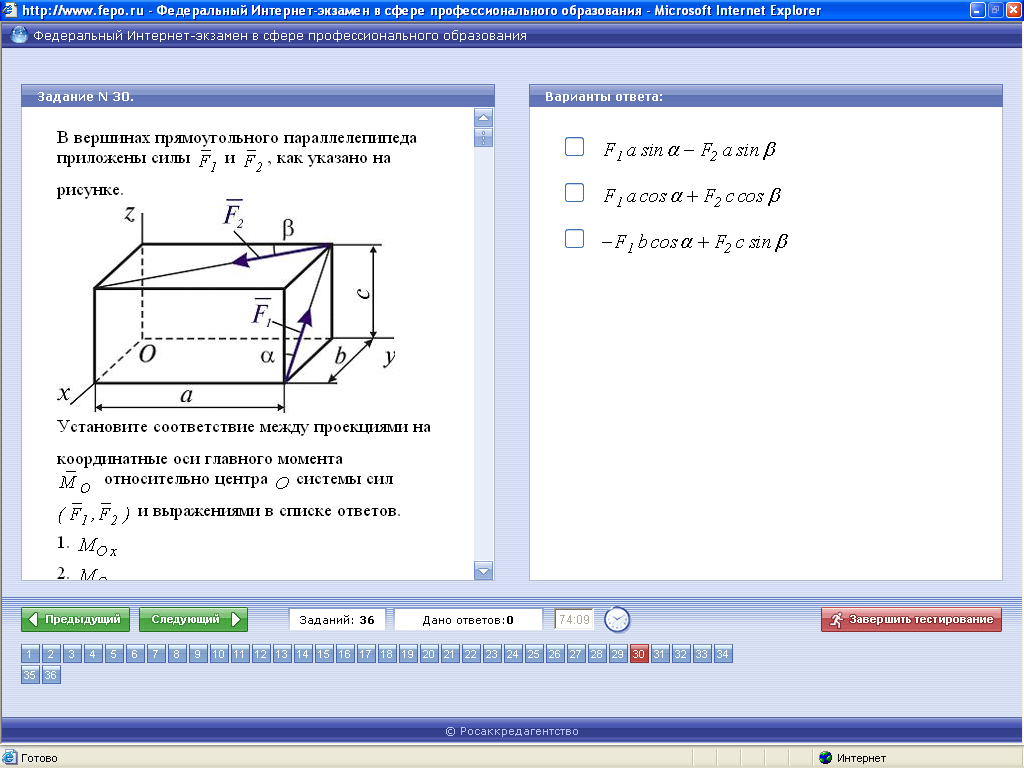
 относительно центра О на координатные оси, как известно, можно получить просуммировав моменты всех сил системы относительно этих координатных осей:
относительно центра О на координатные оси, как известно, можно получить просуммировав моменты всех сил системы относительно этих координатных осей:

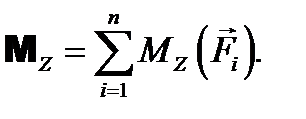
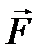 на плоскость, перпендикулярную оси.
на плоскость, перпендикулярную оси.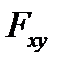 на ее плечо
на ее плечо 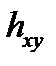 относительно точки пересечения оси с плоскостью.
относительно точки пересечения оси с плоскостью.