
|
|
Решение уравнений геометрического анализа
OA*cosq=Xd+DB*cosf3+ABcosf2
OA*sinq=Yd+DB*sinf3+ABsinf2
(OA*cosq-Xd)^2 = (DB*cosf3+BA*cosf2)^2
(OA*sinq-Yd)^2 = (DB*sinf3+BA*sinf2)^2
(OA*cosq-Xd)^2+(OA*sinq-Yd)^2 =BD^2+AB^2+2BD*BA*(cosf2*cosf3+sinf2*sinf3)
f2=f23+f3
OA*cosq=Xd+BD*cosf3+BD*cosf23*cosf3-BA*sinf23*sinf3
OA*sinq=Yd+BD*sinf3+BA*sinf23-cosf3+BA*sinf3*cosf23
Особое положение:
OA*sinq=Yd+DB*sinf3+ABsinf2 В неявной форме:
F1= Xd+DB*cosf3+ABcosf2-OA*cosq F2= Yd+DB*sinf3+ABsinf2-OA*sinq
Частные производные
dF1/df3= -DBsinf3 dF2/df3= BDcosf3 dF1/df2= -ABsinf2 dF2/f2= AB*cosf3
Определитель матрицы Якоби
J=cos(f2-f3)=0
f2=f3– особое положение группы ВВВ Особое положение группы ВВВ
Xe+BE*cosy4=OA*cosq-AB*cosf2
Ye+BE*sinf4=OA*sinq-AB*sinf2
Ye(q) = OA*sinq-AB*sinf2-BE*sinf4
Xe+BE*cosf4=OA*cosq-AB*cosf2
Ye+BE*sinf4=OA*sinq-AB*sinf2 В неявной форме F1= OA*cos(q)-AB*cosf2(q)-Xe-Be*cosf4(q) F2=OA*sin(q)-AB*sinf2(q)-Ye-Be*sinf4(q) Частные производные dF1/df4=+BEsinf4 dF2/df4=-BEcosf4 dF1/Ye=0 dF2/Ye=1 Определитель матрицы Якоби J=BEsinf4=0 f4=0 град – особое положение группы ВВП Особое положение группы ВВП
Исследование функций положения (определение хода, зон холостого хода, зон рабочего хода)
Сравнение по выбранным критериям
Приведем максимальные значения коэффициентов
Для определения коэффициента К1 нам необходимо знать максимальное значение скорости выходного звена, для находим скорость точки Е и строим ее график.
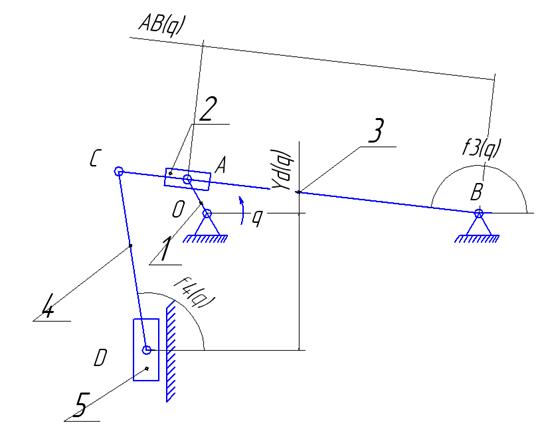
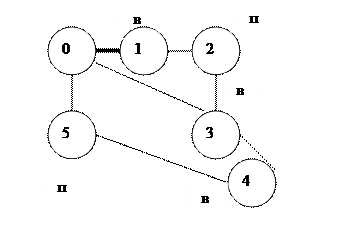
ВТОРОЙ ПРОТОТИП Схема механизма
Длины звеньев (м)
с – коэффициент параметризации Структурный анализ механизма
Число подвижных звеньев механизма N=5. Количество кинематических пар механизма P=7. Суммарное число подвижностей всех кинематических пар S=7. Число независимых контуров графа K=P-N=2. Степень подвижности механизма W=S-3K=7-6=1. Механизм нормальный, т.к. n=W. Составление уравнений геометрического анализа
OAsinq = Yb+AB*sinf3
2) Yd+CD*sinf4=Yb+BC*sinf3(q) Исследование функций положения (определение хода, зон холостого хода, зон рабочего хода)
Сравнение по выбранным критериям Приведем максимальные значения коэффициентов Для определения коэффициента К1 нам необходимо знать максимальное значение скорости выходного звена, для находим скорость точки D и строим ее график.
Выводы
Из таблицы видно, что наиболее подходящим по данным критериям является 1 прототип, так как он обладает меньшим коэффициентом К1, наиболее приближенным к заданному значению ходу рабочего звена. Следовательно, выбираю первый механизм. Кинематический анализ механизмов. Задача кинематического анализа. Задачей кинематического анализа является определение скоростей и ускорений точек механизма угловых скоростей и угловых ускорений его звеньев при заданных первых и вторых производных по времени от обобщенных координат. Нахождение скоростей и ускорений звеньев механизма Аналог скорости – первая производная по обобщающей координате q.
OAsinq = Yd + BDsinf3 + ABsinf2 Дифференцируем первую систему по q:
OAcosq = CDcosf3∙f31 + ACcosf2∙f21 По методу Крамера определяем аналоги скоростей:
Аналог ускорения – вторая производная по обобщенной координате q:
-OAsinq = -CDsinf3∙f31^ 2 +CDcosf3∙f311 - ACsinf2∙f21^2+ ACcosf2∙f211
CDsinf3∙f3^ 2 +ACsinf2∙f21^2-OAsinq = CDcosf3∙f311 +ACcosf2∙f211
По методу Крамера определяем аналоги ускорений:
Ye+BE*sinf4=OA*sinq-AB*sinf2
-BE*sinf4(q)*f41(q)= -OA*sin(q)+AB*sinf2(q)*f21(q)
Ye1(q)+BE*cosf4(q)*f41(q)= OA*cos(q)-AB*cosf2(q)*f21(q) f41(q) = (-OA*sin(q)-AB*cosf2(q)*f21(q))/-BE*sinf4(q) Ye1(q) = OA*cos(q)-AB*cosf2(q)*f21(q)-BE*cosf4(q)*f41(q) Снова дифференцируем по q:
Ye11-BE*sinf4*f41^2+BE*cosf4*f411= -OA*sinq+AB*sinf2*f21^2-AB*cosf2*f211
f411(q) = (- OAcos(q)+AB*cosf2(q)*f21(q)^2+AB*sinf2(q)*f211(q)+BE*cosf4(q)*f41(q)^2)/-BE*sinf4(q)
Ye11(q) = -OA*sin(q)+AB*sinf2(q)*f21(q)^2-AB*cosf2(q)*f211(q)+BE*sinf4(q)*f41(q)^2-BE*cosf4(q)*f411(q)
Графоаналитическое исследование кинематики механизмов. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Первыя система :
Первыя система :



 OA*cosq=Xd+DB*cosf3+ABcosf2
OA*cosq=Xd+DB*cosf3+ABcosf2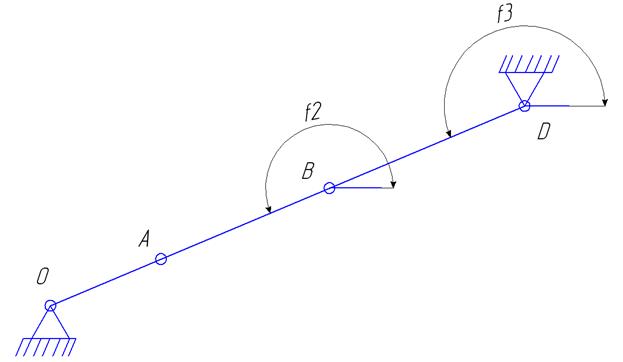
 Вторая система:
Вторая система:
 Особое положение
Особое положение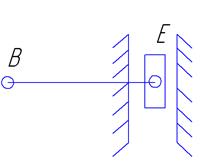











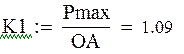






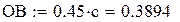




 1) OAcosq = Xb+AB*cosf3
1) OAcosq = Xb+AB*cosf3 Xd+CD*cosf4=Xb+BC*cosf3(q)
Xd+CD*cosf4=Xb+BC*cosf3(q)



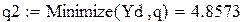





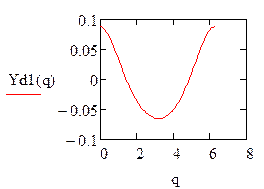




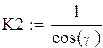

 1) OAcosq = Xd + BDcosf3 + ABcosf2
1) OAcosq = Xd + BDcosf3 + ABcosf2

 -OAcosq = -CDcosf3∙f31^2 -CDsinf3∙f311 - ACcosf2∙f21^2- ACsinf2∙f211
-OAcosq = -CDcosf3∙f31^2 -CDsinf3∙f311 - ACcosf2∙f21^2- ACsinf2∙f211

 Дифференцируем вторую систему по q:
Дифференцируем вторую систему по q: -BE*cosf4*f41^2-BE*sinf4*f411= -AB*cosq+AB*cosf2*f21^2+AB*sinf2*f211
-BE*cosf4*f41^2-BE*sinf4*f411= -AB*cosq+AB*cosf2*f21^2+AB*sinf2*f211