
|
|
Условные силы, действующие на шатунные шейки коленчатого вала от двух смежных шатунов
Коленчатый вал двигателя полноопорный с кривошипами, расположенными в вертикальной и горизонтальной плоскостях. Порядок работы двигателя 1-5-4-2-6-3-7-8. Чередование вспышек равномерное через 90˚. В соответствии с порядком работы двигателя на 1, 2 и 3-ю шатунные шейки одновременно действуют силы от левого и правого шатунов, смещенные одна относительно другой на 90˚, а на 4-ю шейку действуют силы от левого и правого шатунов, смещенные на 450˚. Суммарные тангенциальные силы, действующие на шатунные шейки от двух смежных шатунов: Суммарные силы, действующие на шатунные шейки по радиусу кривошипа от двух смежных шатунов: Условные суммарные силы, действующие на шатунные шейки, строят при условии, что во всех левых цилиндрах отсчет углов начинается от 0˚. Силы TΣ и KΣ рассчитываем табличным методом (табл. 6.3). Таблица 6.3
По полученным данным строим условные полярные диаграммы суммарных сил Диаграммы сил SΣ1(2,3) и SΣ4 с центрами в точках Oш1(2,3) и Oш4 Значения сил Rш.шΣ1(2,3) и Rш.шΣ4 для различных φ заносим в таблицу 6.3 и по ним строим диаграммы Rш.шΣ1(2,3) и Rш.шΣ4 в прямоугольных координатах. Масштабы развернутой диаграммы: По развернутым диаграммам определяем:
где OB – длина диаграммы, мм; F – площадь под кривой Rш.ш, мм2. По полярной диаграмме строим диаграмму износа 1-ой шатунной шейки. Сумму сил Rш.шi, действующих по каждому лучу диаграммы износа (от 1 до 12), определяем с помощью таблицы 6.4. По данным таблицы 6.4 в масштабе Таблица 6.4
Силы, действующие на колена вала
Суммарные силы, действующие на колена вала по радиусу кривошипа: Полярные диаграммы сил Rш.шΣ1(2,3) и Rш.шΣ4 с центрами в точках Oк1(2,3) и Oк4
Уравновешивание
Силы инерции первого порядка взаимно уравновешиваются где a =253 мм – расстояние между центрами шатунных шеек. Равнодействующие сил инерции второго порядка для каждой секции двигателя всегда направлены по горизонтали перпендикулярно оси коленчатого вала. Сумма этих равнодействующих сил равна нулю: Суммарный момент сил инерции второго порядка также равен нулю: Суммарный момент
Уравновешивание моментов Расчет деталей двигателя
Расчет поршня
Поршень воспринимает высокие газовые, инерционные и тепловые нагрузки. Его основными функциями являются уплотнение внутрицилиндрового пространства и передачи газовых сил давления кривошипно-шатунному механизму. Поверочный расчет элементов поршня осуществляется без учета переменных нагрузок, величина которых учитывается при установлении соответствующих допускаемых напряжений.
С учетом соотношений, приведенных в табл. 12.1 [1], принимаем: толщину днища поршня δ=19 мм, высоту поршня H=160 мм, высоту юбки поршня hю=83 мм, радиальную толщину кольца t=5,4 мм, радиальный зазор кольца в канавке поршня Δt=0,8 мм, толщину стенки головки поршня s=10 мм, толщину верхней кольцевой перемычки hп=6,4 мм, число и диаметр масляных каналов в поршне nм=8 и dм=1,5 мм (рис. 8.1). Материал поршня – эвтектический алюминиевый сплав с содержанием кремния около 12%, коэффициент линейного расширения αп=22∙10-6 1/К, материал гильзы цилиндра – серый чугун, αц=11∙10-6 1/К. Напряжения сжатия в сечении x – x: площадь сечения x – x где
максимальная сжимающая сила напряжение сжатия где [σсж]=30-40 МПа – допустимое напряжение на сжатие для алюминиевого поршня. Напряжения разрыва в сечении x – x: максимальная угловая скорость холостого хода
масса головки поршня с кольцами, расположенными выше сечения x – x
максимальная разрывающая сила напряжение разрыва Напряжение в верхней кольцевой перемычке: среза изгиба сложное Удельное давление поршня на стенку цилиндра:
Ускорение приработки юбки поршня, также уменьшение трения и снижения износа пары – юбка поршня – стенка цилиндра – достигается покрытием юбки поршня тонким (0,003 – 0,005 мм) слоем олова, свинца или оловянно-свинцового сплава. Гарантированная подвижность поршня в цилиндре достигается за счет установления оптимальных диаметральных зазоров между цилиндром и поршнем при их неодинаковом расширении в верхнем сечении головки поршня Δг’ и нижнем сечении юбки Δю’. Диаметры головки и юбки поршня с учетом монтажных зазоров:
где Диаметральные зазоры в горячем состоянии соответственно между стенкой цилиндра и головкой поршня и между стенкой цилиндра и юбкой поршня
где Tц=388 К, Tг=493 К, Tю=428 К – соответственно температура стенок цилиндра, головки и юбки поршня в рабочем состоянии, принятые с учетом жидкостного охлаждения двигателя; T0=293 К – начальная температура цилиндра и поршня. Т.к. Δг’>0 и Δю’>0 (натяг отсутствует), то поршень пригоден к работе.
Расчет поршневого кольца
Поршневые кольца работают в условиях высоких температур и значительных переменных нагрузок, обеспечивая герметизацию надпоршневого пространства, отвод избыточной доли теплоты от поршня в стенки цилиндра, рациональное распределение масляного слоя по зеркалу цилиндра и ограничения попадания масла в камеру сгорания. Материал кольца – серый чугун, E=1∙105 МПа. Среднее давление кольца на стенку цилиндра
где Давление (МПа) кольца на стенку цилиндра в различных точках окружности при каплевидной форме эпюры давления Результаты расчета p, а также μк для различных углов ψ приведены ниже. По этим данным построена каплевидная эпюра давлений кольца на стенку цилиндра (рис. 8.2).
Напряжения изгиба при надевании кольца на поршень
где m=1,57 – коэффициент, зависящий от способа надевания кольца. Монтажный зазор в замке поршневого кольца в холодном состоянии
где Δ’к=0,08 мм – минимально допустимый зазор в замке кольца во время работы двигателя, αк=αц=11∙10-6 1/К – коэффициенты линейного расширения материала кольца и гильзы цилиндра, Tц=388 К, Tк=498 К – соответственно температура стенок цилиндра, кольца в рабочем состоянии, принятые с учетом жидкостного охлаждения двигателя; T0=293 К – начальная температура.
Расчет поршневого пальца
Во время работы двигателя поршневой палец подвергается воздействию переменных нагрузок, приводящих к возникновению напряжений изгиба, сдвига, смятия и овализации. Принимаем наружный диаметр пальца dп=45 мм, внутренний диаметр пальца dв=27 мм, длину пальца lп=112 мм, длину втулки шатуна lш=38 мм, расстояние между торцами бобышек b=51 мм. Материал поршневого пальца – сталь 12ХН3А, E=2,2∙105 МПа. Палец закрепленного типа. Расчетная сила, действующая на поршневой палец: газовая инерционная где расчетная где k=0,72 – коэффициент, учитывающий массу поршневого пальца. Удельное давление пальца на втулку поршневой головки шатуна Удельное давление пальца на бобышки Напряжение изгиба в среднем сечении пальца при распределении нагрузки по длине пальца согласно эпюре на рис. 8.3:
Касательные напряжения среза в сечениях между бобышками и головкой шатуна
Вследствие неравномерного распределения сил, приложенных к пальцу (принимается синусоидальное распределение нагрузки по поверхности пальца – рис. 8.3, а), при работе двигателя происходит деформация сечения пальца (овализация). Наибольшее увеличение горизонтального диаметра пальца при овализации
Напряжения овализации на внешней поверхности пальца (рис. 8.3, б): в горизонтальной плоскости (точки 1, ψ=0˚)
в вертикальной плоскости (точки 3, ψ=90˚)
в горизонтальной плоскости (точки 2, ψ=0˚)
в вертикальной плоскости (точки 4, ψ=90˚)
Наибольшее напряжение овализации возникает на внутренней поверхности пальца в горизонтальной плоскости, оно не должно превышать 300-350 МПа.
Расчет коленчатого вала
При расчете коленчатого вала принимается, что: кривошип свободно лежит на опорах; опоры и точки приложения сил проходят через средние плоскости шеек; весь пролет между опорами представляет собой абсолютно жесткую балку. На основании данных динамического расчета имеем: коленчатый вал с симметричными коленами, с противовесами, расположенными только на концах вала; центробежная сила инерции вращающихся масс По табл. 11.2 и 11.4 [1] для углеродистой стали 50Г определяем: пределы прочности σв=800 МПа и текучести σт=370 МПа и τт=250 МПа; пределы усталости (выносливости) при изгибе σ-1=340 МПа, растяжении – сжатии коэффициенты приведения цикла при изгибе ασ=0,18, кручении ατ=0,08 и растяжении – сжатии ασ=0,14. По формулам определяем: при изгибе при растяжении – сжатии
при кручении Удельное давление на поверхности шатунных шеек
где Расчет коренной шейки. Момент сопротивления коренной шейки кручению
Максимальное и минимальное касательные напряжения коренной шейки:
Среднее напряжение и амплитуды напряжений:
где Так как
Расчет шатунной шейки. Момент сопротивления кручению шатунной шейки
Максимальное и минимальное касательные напряжения шатунной шейки:
Среднее напряжение и амплитуды напряжений:
где Так как
Моменты, изгибающие шатунную шейку двухпролетного коленчатого вала (рис. 8.4): в плоскости, перпендикулярной плоскости колена, для сечения I – I по оси масляного отверстия
для среднего сечения B – B
где
в плоскости колена для сечения I – I подсчет не производим, т.к. на основании анализа полярной диаграммы и диаграммы износа масляное отверстие на шатунной шейке целесообразно сделать в горизонтальной плоскости (φм=90˚) и, следовательно, для среднего сечения B – B
где
расчет моментов Максимальные и минимальные нормальные напряжения в шатунной шейке: в сечении I – I
где в сечении B – B
Среднее напряжение и амплитуда напряжений: для сечения I – I
где Таблица 8.1
для сечения B – B
где Запас прочности шатунной шейки от нормальных напряжений определяется для сечения I – I – по пределу усталости (при σм<0)

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
.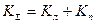 .
. , действующих на 1 (2, 3)-ю и 4-ю шатунные шейки от каждой пары смежных шатунов. Масштаб диаграмм
, действующих на 1 (2, 3)-ю и 4-ю шатунные шейки от каждой пары смежных шатунов. Масштаб диаграмм 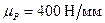 .
. являются соответственно полярными диаграммами условных нагрузок на 1, 2 и 3-ю шатунные шейки – Rш.шΣ1(2,3) и на 4-ю шатунную шейку - Rш.шΣ4.
являются соответственно полярными диаграммами условных нагрузок на 1, 2 и 3-ю шатунные шейки – Rш.шΣ1(2,3) и на 4-ю шатунную шейку - Rш.шΣ4. и
и 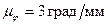 .
. ;
; 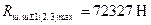 ;
; 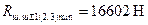 ;
; ;
; 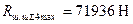 ;
; 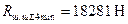 ,
,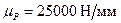 по каждому лучу откладываем величины суммарных сил ΣRш.шi в мм от окружности к центру. По диаграмме износа определяем положение оси масляного отверстия φм=90˚.
по каждому лучу откладываем величины суммарных сил ΣRш.шi в мм от окружности к центру. По диаграмме износа определяем положение оси масляного отверстия φм=90˚. .
. являются соответственно полярными диаграммами нагрузок на колена вала RкΣ1(2,3) и RкΣ4. Значения RкΣ1(2,3) и RкΣ4 для различных φ заносим в табл. 6.3.
являются соответственно полярными диаграммами нагрузок на колена вала RкΣ1(2,3) и RкΣ4. Значения RкΣ1(2,3) и RкΣ4 для различных φ заносим в табл. 6.3. Проектируемый однорядный шестицилиндровый двигатель имеет следующий порядок работы цилиндров: 1-5-4-2-6-3-7-8. Промежутки между вспышками равны 90˚. Угол развала цилиндров γ=90˚. Коленчатый вал имеет кривошипы, расположенные в двух взаимно перпендикулярных плоскостях (рис. 7.1).
Проектируемый однорядный шестицилиндровый двигатель имеет следующий порядок работы цилиндров: 1-5-4-2-6-3-7-8. Промежутки между вспышками равны 90˚. Угол развала цилиндров γ=90˚. Коленчатый вал имеет кривошипы, расположенные в двух взаимно перпендикулярных плоскостях (рис. 7.1).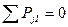 . Суммарный момент этих сил действует во вращающейся плоскости, составляющей с плоскостью первого кривошипа угол 18˚26’:
. Суммарный момент этих сил действует во вращающейся плоскости, составляющей с плоскостью первого кривошипа угол 18˚26’: 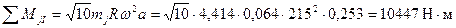 ,
, .
. . Центробежные силы инерции для всех секций равны и направлены попарно в разные стороны. Равнодействующая этих сил
. Центробежные силы инерции для всех секций равны и направлены попарно в разные стороны. Равнодействующая этих сил 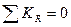 .
.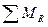 центробежных сил действует в той же плоскости, что и равнодействующий момент сил инерции первого порядка
центробежных сил действует в той же плоскости, что и равнодействующий момент сил инерции первого порядка 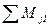 :
: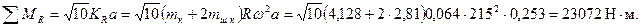
 На основании данных расчетов (теплового, скоростной характеристики и динамического) получили: диаметр цилиндра D=128 мм, ход поршня S=128 мм, максимальное давление сгорания pZ=8,56 МПа при nN=2200 об/мин, площадь поршня Fп=129 см2, наибольшую нормальную силу
На основании данных расчетов (теплового, скоростной характеристики и динамического) получили: диаметр цилиндра D=128 мм, ход поршня S=128 мм, максимальное давление сгорания pZ=8,56 МПа при nN=2200 об/мин, площадь поршня Fп=129 см2, наибольшую нормальную силу 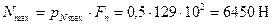 при φ=380˚, массу поршневой группы
при φ=380˚, массу поршневой группы 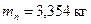 , частоту вращения nх.х.max=2100 об/мин и λ=0,27.
, частоту вращения nх.х.max=2100 об/мин и λ=0,27. ,
,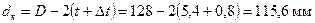 ,
,  ,
,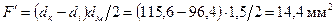 ;
;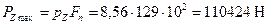 ,
,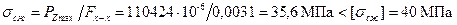 ,
,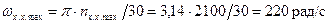 ;
;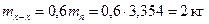 ;
;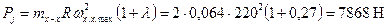 ;
;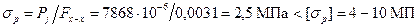 .
.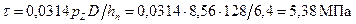 ;
; ;
; .
.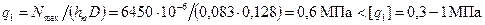 ;
;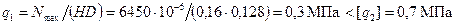 .
.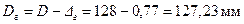 ;
;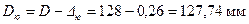 ,
,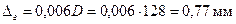 ;
; 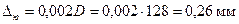 .
.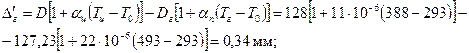
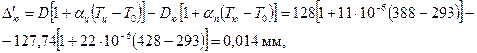
 ,
,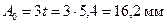 – разность между величинами зазоров замка кольца в свободном и рабочем состоянии.
– разность между величинами зазоров замка кольца в свободном и рабочем состоянии. , где μк – переменный коэффициент, определяемый изготовителем в соответствии с принятой формой эпюры давления кольца на зеркало цилиндра.
, где μк – переменный коэффициент, определяемый изготовителем в соответствии с принятой формой эпюры давления кольца на зеркало цилиндра.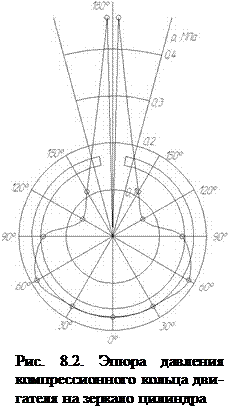 Напряжение изгиба кольца, возникающее в сечении кольца, противоположном замку в рабочем состоянии
Напряжение изгиба кольца, возникающее в сечении кольца, противоположном замку в рабочем состоянии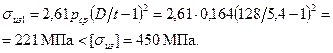
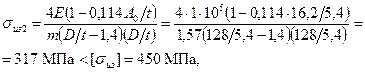
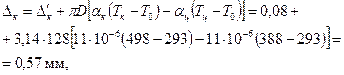
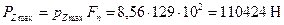 ,
,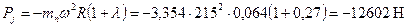 ,
, ,
,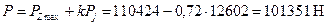 ,
,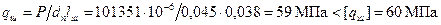 .
.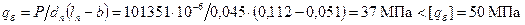 .
. где
где 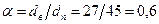 .
.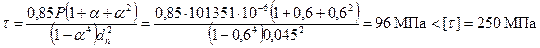 .
.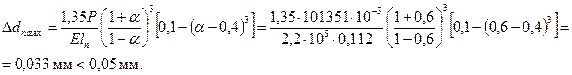
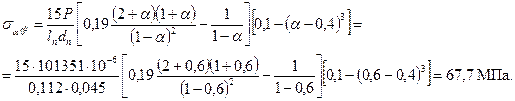
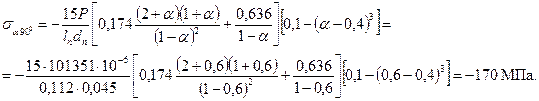

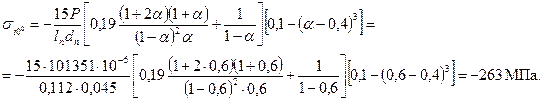
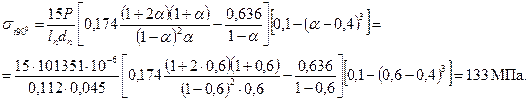
 Коленчатый вал – наиболее сложная в конструктивном отношении и наиболее напряженная деталь двигателя, воспринимающая периодические нагрузки от сил давления газов, сил инерции и их моментов. Действие этих сил и моментов приводит к возникновению в материале коленчатого вала значительных напряжений скручивания, изгиба и растяжения – сжатия.
Коленчатый вал – наиболее сложная в конструктивном отношении и наиболее напряженная деталь двигателя, воспринимающая периодические нагрузки от сил давления газов, сил инерции и их моментов. Действие этих сил и моментов приводит к возникновению в материале коленчатого вала значительных напряжений скручивания, изгиба и растяжения – сжатия.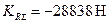 ; радиус кривошипа R=64 мм. С учетом соотношений, приведенных в табл. 14.1 [1], принимаем следующие основные размеры колена вала (рис. 8.4): коренная шейка – наружный диаметр dк.ш=93 мм, длина lк.ш=74 мм; шатунная шейка – наружный диаметр dш.ш=89 мм, внутренний диаметр δш.ш=33 мм, длина lш.ш=115 мм; расчетное сечение A – A щеки – ширина b=147 мм, толщина h=32 мм; радиус галтелей
; радиус кривошипа R=64 мм. С учетом соотношений, приведенных в табл. 14.1 [1], принимаем следующие основные размеры колена вала (рис. 8.4): коренная шейка – наружный диаметр dк.ш=93 мм, длина lк.ш=74 мм; шатунная шейка – наружный диаметр dш.ш=89 мм, внутренний диаметр δш.ш=33 мм, длина lш.ш=115 мм; расчетное сечение A – A щеки – ширина b=147 мм, толщина h=32 мм; радиус галтелей 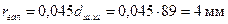 . Материал вала – сталь 50Г.
. Материал вала – сталь 50Г.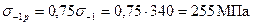 и кручении
и кручении 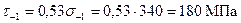 ;
;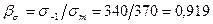 и
и 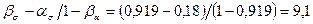 ;
;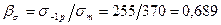 и
и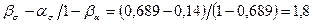 ;
;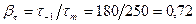 и
и 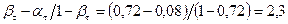 .
.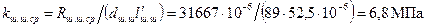 ;
;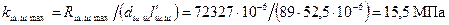 ,
, ;
;  – соответственно средняя и максимальная нагрузки на шатунную шейку;
– соответственно средняя и максимальная нагрузки на шатунную шейку; 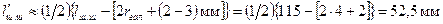 – рабочая ширина одного шатунного вкладыша.
– рабочая ширина одного шатунного вкладыша.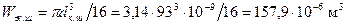 .
.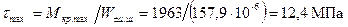 ;
; .
.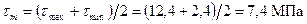 ;
; ;
;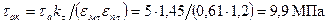 ,
,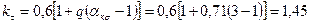 – эффективный коэффициент концентрации напряжений; q=0,71 – коэффициент чувствительности материала к концентрации напряжений, принятый по данным §11.3 [1]; αкσ=3 – теоретический коэффициент концентрации напряжений, определенный по табл. 11.6 [1] с учетом наличия в шейке масляного отверстия; εмτ=0,61 – масштабный коэффициент, определенный по табл. 11.7 [1] при dк.ш=93 мм, εпτ=1,2 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] с учетом закалки шеек токами высокой частоты.
– эффективный коэффициент концентрации напряжений; q=0,71 – коэффициент чувствительности материала к концентрации напряжений, принятый по данным §11.3 [1]; αкσ=3 – теоретический коэффициент концентрации напряжений, определенный по табл. 11.6 [1] с учетом наличия в шейке масляного отверстия; εмτ=0,61 – масштабный коэффициент, определенный по табл. 11.7 [1] при dк.ш=93 мм, εпτ=1,2 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] с учетом закалки шеек токами высокой частоты.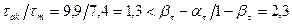 , то запас прочности коренной шейки от касательных напряжений определяем по пределу текучести:
, то запас прочности коренной шейки от касательных напряжений определяем по пределу текучести: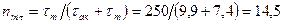 .
.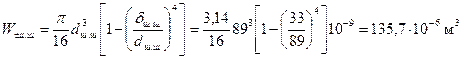 .
.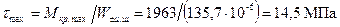 ;
;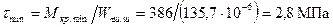 .
.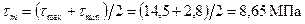 ;
;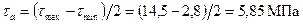 ;
;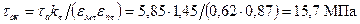 ,
,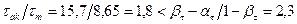 , то запас прочности шатунной шейки от касательных напряжений определяем по пределу текучести:
, то запас прочности шатунной шейки от касательных напряжений определяем по пределу текучести: .
.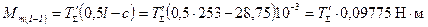 ;
; ,
,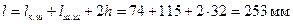 ;
; 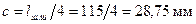 ;
;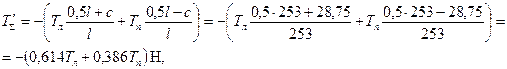
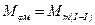 ;
; ,
, ;
;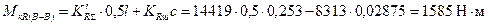 ;
; ;
;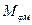 и
и 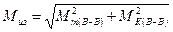 приведен в табл. 8.1, где значения Tл, Tп, Kл и Kп взяты из табл. 6.3.
приведен в табл. 8.1, где значения Tл, Tп, Kл и Kп взяты из табл. 6.3. ;
;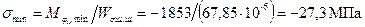 ,
,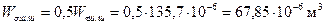 ;
;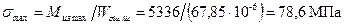 ;
;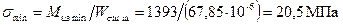 .
.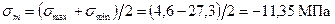 ;
; ;
; ,
, – эффективный коэффициент концентрации напряжений; q=0,71 – коэффициент чувствительности материала к концентрации напряжений, принятый по данным §11.3 [1]; αкσ=3 – теоретический коэффициент концентрации напряжений, определенный по табл. 11.6 [1] с учетом наличия в шейке масляного отверстия; εмσ=0,67 – масштабный коэффициент, определенный по табл. 11.7 [1] при dш.ш=89 мм, εпσ=0,87 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] для внутренней поверхности шейки (сверления), на которую выходит масляное отверстие;
– эффективный коэффициент концентрации напряжений; q=0,71 – коэффициент чувствительности материала к концентрации напряжений, принятый по данным §11.3 [1]; αкσ=3 – теоретический коэффициент концентрации напряжений, определенный по табл. 11.6 [1] с учетом наличия в шейке масляного отверстия; εмσ=0,67 – масштабный коэффициент, определенный по табл. 11.7 [1] при dш.ш=89 мм, εпσ=0,87 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] для внутренней поверхности шейки (сверления), на которую выходит масляное отверстие;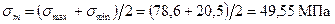 ;
;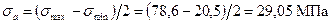 ;
;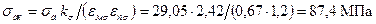 ,
,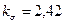 ; εмσ=0,67 (как для сечения I – I); εпσ=1,2 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] с учетом закалки шеек токами высокой частоты.
; εмσ=0,67 (как для сечения I – I); εпσ=1,2 – коэффициент поверхностной чувствительности, определенный по табл. 11.8 [1] с учетом закалки шеек токами высокой частоты. ;
;