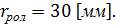|
|
Простые зубчатые механизмы
7.1 Структурный анализ простого зубчатого механизма
Структурный анализ простых зубчатых механизмов сводится к определению подвижности механизма.
Таблица 8 - звенья простого зубчатого механизма
Подвижность механизма определяемпо формуле Чебышева:
где
В структуру механизма входят два подвижных звена (Таблица 9) и стойка, представленная двумя шарнирно-неподвижными опорами. Следовательно,
Таблица 9 –кинематические пары простого зубчатого механизма
Из таблицы 9 видно, что кинематические пары 0-1 и 0-2 являются вращательными парами пятого класса, следовательно, р1=2. Кинематическая пара 1-2 является парой 4 класса, р2=1. Подставим число подвижных звеньев и число пар пятого и четвертого классов в формулу Чебышева:
Полученный результат означает, что для однозначного описания
положения всех звеньев механизма в рассматриваемой плоскости достаточно
задать одну обобщенную координату. 7.2 Синтез эвольвентного зацепления простого зубчатого механизма Найдем инвалюту угла зацепления:
По таблице значений инвалют найден угол зацепления:
Найдем минимальную величину коэффициента смещения для шестерни:
Найдем коэффициент смещения для колеса:
Отложим значения смещения Найдем геометрические параметры зубчатых колес. Диаметры делительных окружностей:
для шестерни
для колеса
где
Диаметры начальных окружностей:
для шестерни: для колеса: Шаг по делительной окружности:
Шаг по основной окружности:
Диаметры основных окружностей: для шестерни: для колеса: Диаметры окружностей впадин зубьев: для шестерни: для колеса: где Диаметры окружностей вершин зубьев:
для шестерни для колеса
где
Коэффициент уравнительного смешения:
Коэффициент воспринимаемого смешения:
Уточненное межосевое расстояние:
Делительное межосевое расстояние:
Толщина зуба по делительной окружности:
для шестерни
для колеса
Толщина впадин по делительной окружности:
для шестерни
для колеса
Высота зубьев:
Углы профиля на окружности вершин:
для шестерни:
для колеса:
Толщина зубьев по окружности вершин:
для шестерни
для колеса
Проверка:
Оба значения толщины зубьев по окружности больше значения минимальной толщины, проверка сходится.
Коэффициент торцевого перекрытия:
Для построения зубчатого зацепления определим масштабный коэффициент длин и переведем все геометрические параметры зубчатых колес в данный масштабный коэффициент.
Переведем все значения через
Для построения зубчатого зацепления отложим межосевое расстояние Начальные окружности Чтобы построить участок активного зацепления, следует на линии активного зацепления обозначить точки А1 и В1, они находятся на пересечении линии зацепления и окружностей радиусами Ra1 и Ra2. Затем радиусом О1А1 и О2А2 проводим окружности. Эти окружности будут нижней границей участка активного зацепления. А верхней границей будут являться окружности радиусом Ra1 и Ra2.
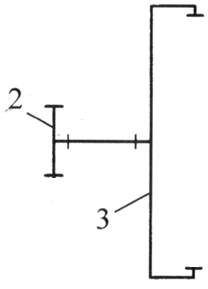
8. Сложный зубчатый механизм. Сложный зубчатый механизм − это зубчатый механизм, образованный числом зубчатых колес больше двух. Таблица 9- звенья сложного зубчатого механизма
Из таблицы видим, что механизм имеет семь подвижных звеньев, совершающих вращательные и сложные движения. Корона 6 является неподвижным звеном и относится к элементам стойки. Для выявления числа, класса, подвижности, вида контакта и замыкания всех кинематических пар составим таблицу:
Таблица 10 – кинематические пары сложного зубчатого механизма
Зубчатый механизм является плоским, следовательно, подвижность определяем по формуле Чебышева:
Анализируя схему, видим, что механизм состоит из стойки 0, представленной пятью шарнирно неподвижными опорами, и пятью подвижными звеньями (1; 2-3; 4- 5; 6-H; 7; 8). Колесо 9 является неподвижным звеном и относится к стойке. Таким образом, Схема содержит шесть одноподвижных кинематических пар: 0-1; 0-2,3; 0-4,5; 0,9-6,Н; 0-7; 6H-8. И пятью высших двухподвижных кинематических пар: 1-2,3; 2,3-4,5; 4,5-6H;;8-9; 7-8. Следовательно, Подставив найденные значения в Чебышева, получим:
Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.
8.1 Синтез сложного зубчатого механизма
Разобьем данный сложный зубчатый механизм на четыре простых зубчатые передачи и, планетарный механизм:
Разложим передаточное число по ступеням (рядам):
Передаточное отношение первого ряда:
тогда Из условия отсутствия интерференции:
Передаточное отношение второго ряда:
тогда Из условия отсутствия интерференции:
Передаточное отношение третьего ряда:
тогда Из условия отсутствия интерференции:
Передаточное отношение планетарного механизма:
Используя условие соосности:
Для обеспечения собираемости однорядного планетарного механизма необходимо проверить условие сборки:
где: p-число полных циклов солнечного колеса (1,2,3…)
Для обеспечения отсутствия контакта сателлитов друг с другом необходимо проверить условие соседства:
0,50 > 0,39 Условия выполняются. В качестве окончательных чисел зубьев зубчатых колес принимаем следующие значения:
Определим диаметры зубчатых колес механизма.
Рассчитаем масштабный коэффициент длин для данной схемы:
Переведем все диаметры в масштабный коэффициент:
Построим кинематическую схему механизма в найденном масштабном коэффициенте. Расстояние между колесами берем произвольным, поскольку оно не влияет на передаточную функцию механизма.
8.2 Кинематический анализ
Построим план скоростей для данной схемы сложного зубчатого механизма.
Угловая скорость на первом колеса дана: Найдем линейную скорость первого колеса:
Найдем масштабный коэффициент скоростей:
где Построим план угловых скоростей методом параллельного переноса годографов с плана скоростей на план угловых скоростей от полюса и до пересечения с осью ω. Расстояния от нуля до найденных точек и есть значения величин угловых скоростей. Составим пропорцию и вычислим их значения.
Определим передаточное число
Вычислим погрешность:
Полученная погрешность меньше допустимых 5%, следовательно расчет и построение сложного зубчатого механизма выполнено верно. Кулачковый механизм 9.1 Структурный анализ Так как все звенья данного механизма лежат в одной плоскости, то его подвижность рассчитывается по формуле Чебышева:
Таблица 11- звенья кулачкового механизма
Механизм состоит из стойки и трех подвижных звеньев: кулачка 1, коромысла 2 и ролика 3. Ролик введен в схему механизма для замены трения скольжения на трение качения, с целью уменьшения интенсивности износа рабочих поверхностей контактирующих звеньев, а также с целью увеличения КПД и ресурса работы механизма. Ролик образует с выходным звеном поступательную кинематическую пару пятого класса. Подвижность этой кинематической пары не изменяет подвижности кулачкового механизма, не влияет на его передаточную функцию, так как является местной подвижностью. Таблица 11- кинематические пары кулачкового механизма
Звенья 1 и 2 образуют со стойкой низшие кинематические пары 0-1; 0-2; подвижность кинематической пары 2-3 является дефектом структуры с местной подвижностью, равной 1, следовательно,
Расчет по формуле Чебышева для типовых кулачковых механизмов с роликом показывает, что подвижность равна двум. Результат говорит о нали- чии дефектов структуры в схемах типовых кулачковых механизмов с роликом, что свидетельствует о наличии двух видов подвижностей разного функционального назначения. Подвижность типового плоского кулачкового механизма с одним ведущим звеном, образующим первичный механизм с подвижностью, равной единице, следовательно, вторая единица подвижности приходится на долю местной подвижности, образованной роликом с выходным звеном: При удалении ролика, получим:
где
Следовательно, подвижность равна:
9.2 Функция аналога пути Для построения диаграммы зависимости перемещения от угла поворота кулачка вычислим перемещение:
где
Ход механизма с коромыслом равен:
Определим масштабный коэффициент оси аналога пути:
где
Определим масштабный коэффициент угла поворота:
где Переведем все фазовые углы в масштабный коэффициент. Фаза удаления:
Фаза верхнего выстоя отсутствует. Фаза сближения:
Фаза нижнего выстоя:
Разобьем фазовые углы удаления и сближения на восемь частей и посчитаем перемещения для каждого значения фазового угла.
Для первого положения:
Переведем полученную величину перемещения в масштабный коэффициент: s w:val="28"/></w:rPr><m:t>РјРј</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>.</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Для остальных положений расчет ведется аналогично. Результаты сведём в таблицу 12. Таблица 12 – Значения перемещения
Для построения диаграммы отложим переведенные в масштабный коэффициент величины перемещений, с учетом того, что в положениях, соответствующих фазе сближения (7 – 13), отрезки откладываем в обратном порядке. 9.3 Функция аналога скорости Для построения диаграммы аналога скорости воспользуемся формулой:
Для первого положения:
Для остальных положений аналогично, их результаты сводим в таблицу 13. Таблица 13 – Значения скоростей
Рассчитаем масштабный коэффициент:
Для построения диаграммы переведем все полученные значения в масштабный коэффициент. Отложим их на диаграмме, с учетом того, что график на фазе сближения должен находиться ниже оси угла.
9.4 Функция аналога ускорения Для построения диаграммы аналога ускорения, применима следующуя формула:
Для первого положения:
Для остальных положений вычисления проводятся аналогично. Результаты сводим в таблицу 14.
Таблица 14 – Значения ускорений
Рассчитаем масштабный коэффициент:
Для построения диаграммы переведем все полученные значения ускорений в масштабный коэффициент оси аналога ускорения. Отложим рассчитанные отрезки на диаграмме. В положениях фазы сближения график изображаем симметрично относительно оси угла. 9.5 Определение радиуса исходного контура. Построение диаграммы угла давления Для определения радиуса исходного контура построим кривую зависимости аналога скорости От точки О, соответствующей нижнему начальному положению коромысла, в направлении его движения будем откладывать перемещения. Через получившиеся точки проведем перпендикуляры из точки Е находящейся на расстоянии l от Длину коромысла l строим в масштабном коэффициенте длин:
Далее проводим касательные к полученной диаграмме под углом Затем через точку Е проводим прямую под углом К характерным точкам диаграммы для определения радиуса исходного контура кулачка (1…13) проведем из точки
Таблица 17 – значения углов давления
9.6 Синтез профиля кулачка Для построения теоретической окружности возьмем точку Каждый из углов Радиус ролика найдем из выражения: s w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Times New Roman"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>РјРј</m:t></m:r></m:e></m:d><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Times New Roman"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>,</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> где Выберем стандартное целое значение из полученного ряда. Возьмем:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
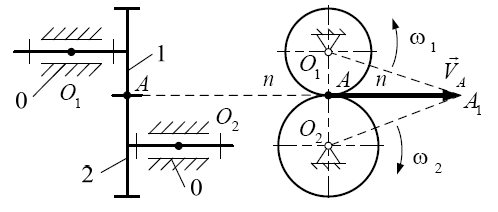


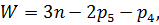
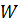 - подвижность механизма;
- подвижность механизма; - число подвижных звеньев;
- число подвижных звеньев; и
и  - соответственно число пар пятого и четвертого класса.
- соответственно число пар пятого и четвертого класса.



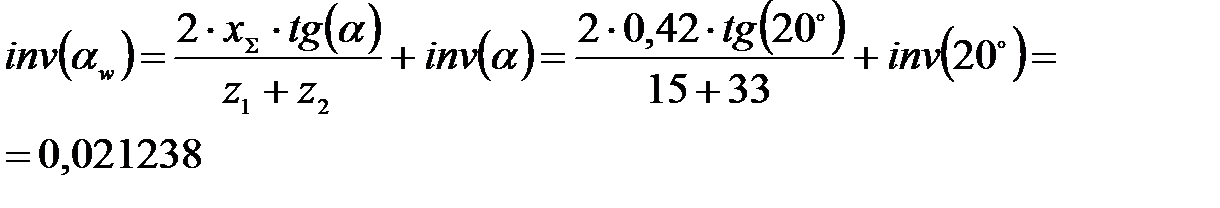
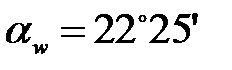

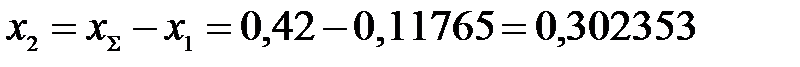
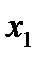 и
и  на соответствующих осях блокирующего контура. Точка их пересечения должна находится в блокирующем контуре. В данном случае точка находится в контуре, следовательно, полученные значения коэффициентов смещения по осям для дальнейших расчетов остаются неизменны.
на соответствующих осях блокирующего контура. Точка их пересечения должна находится в блокирующем контуре. В данном случае точка находится в контуре, следовательно, полученные значения коэффициентов смещения по осям для дальнейших расчетов остаются неизменны.
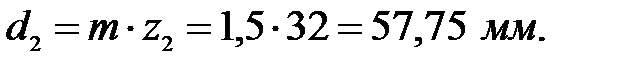
 - модуль;
- модуль; - число зубьев на шестерне и колесе соответственно.
- число зубьев на шестерне и колесе соответственно.
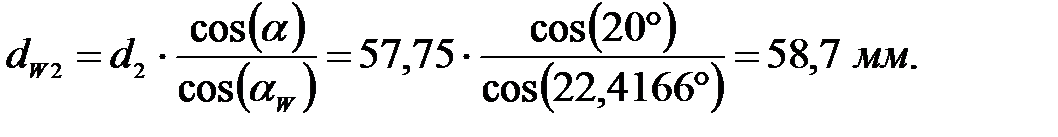
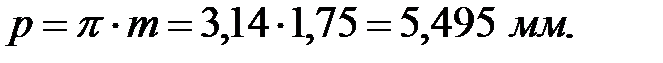
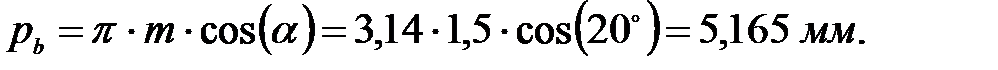
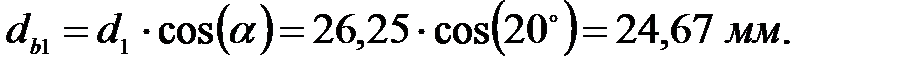
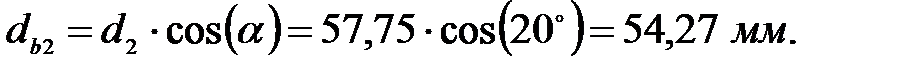
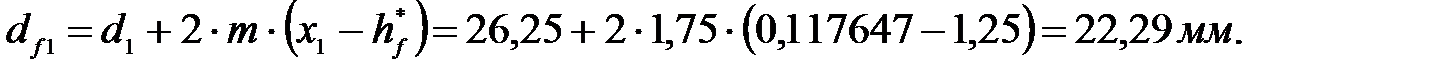
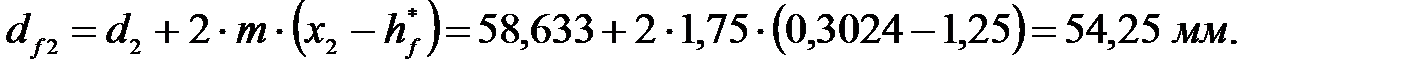
 - коэффициент ножки зуба.
- коэффициент ножки зуба.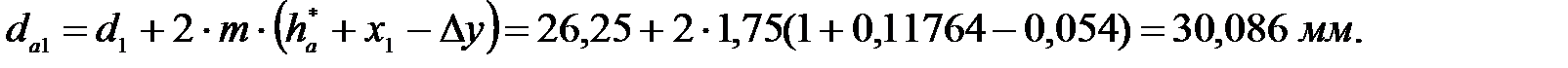
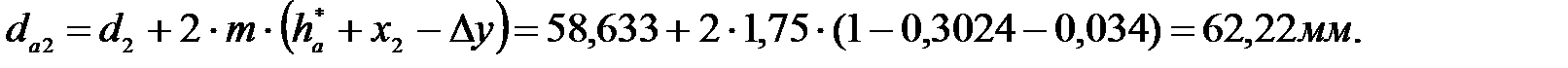
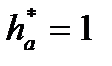 - коэффициент головки зуба.
- коэффициент головки зуба. .
. .
.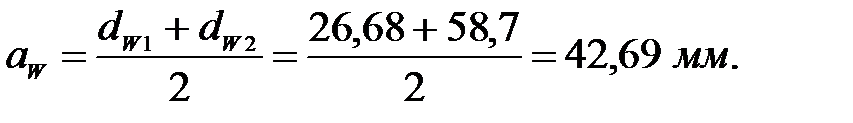
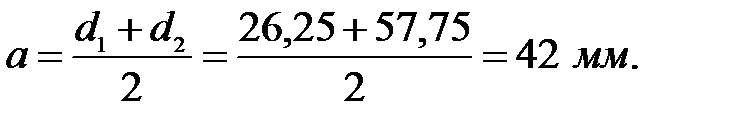

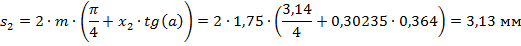
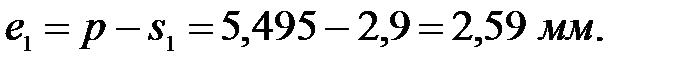
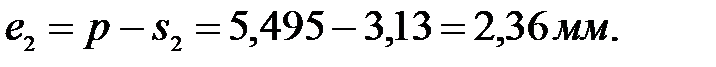
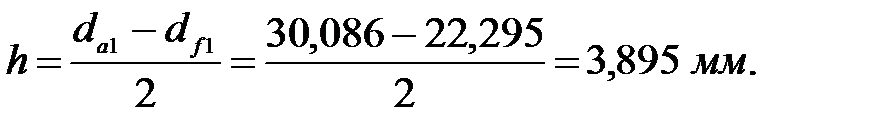
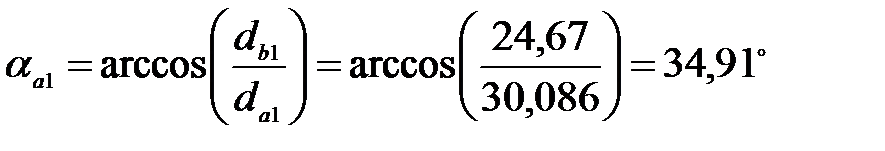
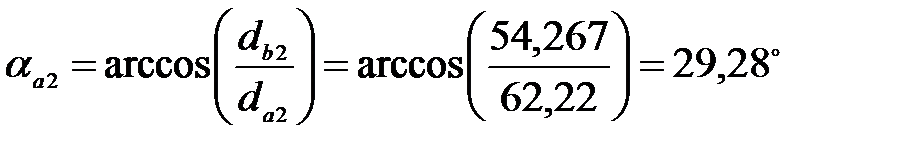

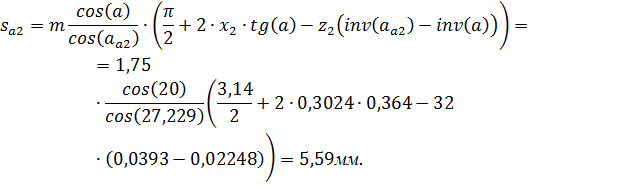
 , где
, где 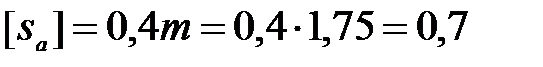
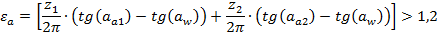
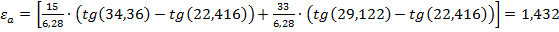
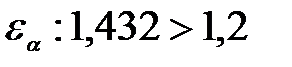
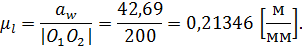
 :
: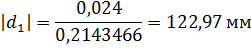
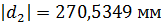
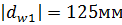
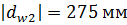
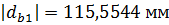
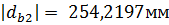

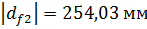
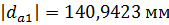
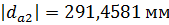
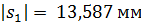
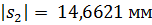
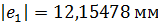
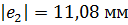
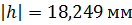
 . Проведем начальную, делительную, основную окружности, а также окружности вершин и впадин зубьев для каждого зубчатого колеса.
. Проведем начальную, делительную, основную окружности, а также окружности вершин и впадин зубьев для каждого зубчатого колеса. и
и  должны сопрягаться в полюсе зацепления P. При выполнении данного условия откладываем под углом
должны сопрягаться в полюсе зацепления P. При выполнении данного условия откладываем под углом  для колеса и для шестерни лучи, пересекающие основные окружности в точках A и B. Через точки A и B проводим прямую - линию зацепления. Она проходит через полюс зацепления P. Отрезок от точки сопряжения P до точки пересечения A, делим на шесть равных частей
для колеса и для шестерни лучи, пересекающие основные окружности в точках A и B. Через точки A и B проводим прямую - линию зацепления. Она проходит через полюс зацепления P. Отрезок от точки сопряжения P до точки пересечения A, делим на шесть равных частей 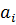 . Проецируем полученные точки на основную окружность, проводим через каждую из них касательную к основной окружности, и на касательных откладываем величину отрезка PA, каждый раз уменьшая на величину t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
. Проецируем полученные точки на основную окружность, проводим через каждую из них касательную к основной окружности, и на касательных откладываем величину отрезка PA, каждый раз уменьшая на величину t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 
















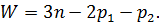
 .
. .
.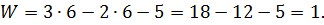
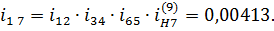

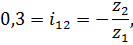

 следовательно
следовательно 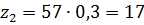
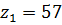
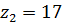
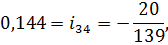
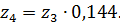
 следовательно
следовательно 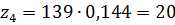
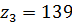
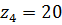
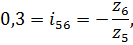
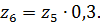
 следовательно
следовательно 
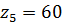
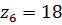




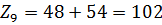
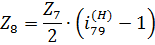
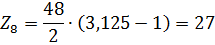
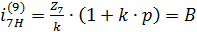
 - целое натуральное число.
- целое натуральное число. - число сателлитов;
- число сателлитов;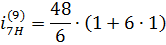
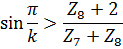
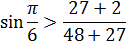
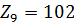
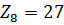
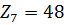


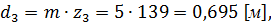

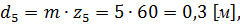



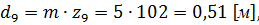

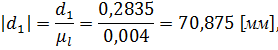
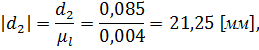
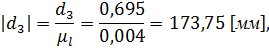
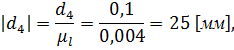
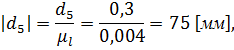
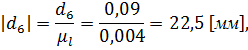
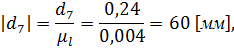
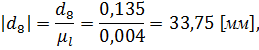
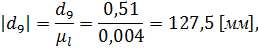
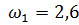
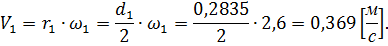
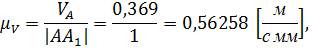
 - отрезок, изображающий скорость точки А на плане скоростей.
- отрезок, изображающий скорость точки А на плане скоростей.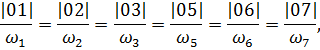
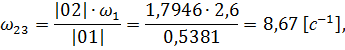

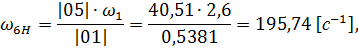
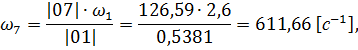
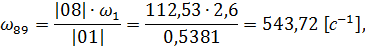
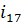 , используя следующую формулу:
, используя следующую формулу: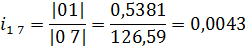
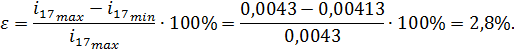

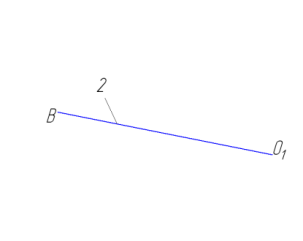






 Кинематическая пара 1-3 является высшей, следовательно,
Кинематическая пара 1-3 является высшей, следовательно,  .
.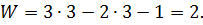
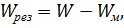
 - подвижность механизма в результате удаления дефектов;
- подвижность механизма в результате удаления дефектов; - местная подвижность.
- местная подвижность.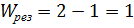
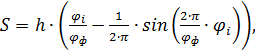
 - перемещение, м;
- перемещение, м; - ход кулачкового механизма, м;
- ход кулачкового механизма, м; - фазовый угол соответствующей фазы, рад;
- фазовый угол соответствующей фазы, рад; - текущее значение фазового угла, рад.
- текущее значение фазового угла, рад.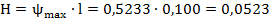
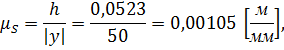
 - расстояние, изображающее максимальное перемещение на диаграмме, мм.
- расстояние, изображающее максимальное перемещение на диаграмме, мм.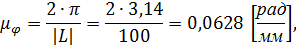
 - произвольно выбранное расстояние, изображающее один период работы механизма на диаграмме, мм.
- произвольно выбранное расстояние, изображающее один период работы механизма на диаграмме, мм.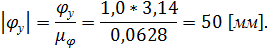
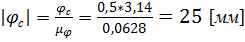 .
.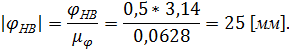
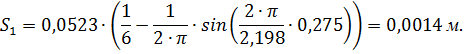
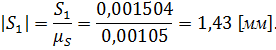

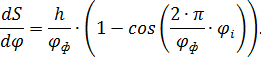
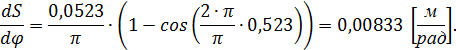

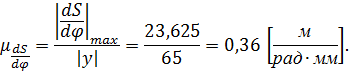

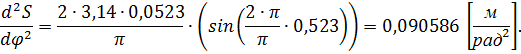

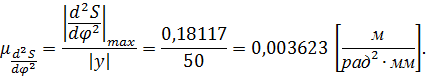
 от перемещения S.
от перемещения S. . Отрезки, значения которых возьмем в миллиметрах, с диаграммы скорости, и отложим их по этим лучам (для фазы удаления в положительную, для фазы сближения в отрицательную сторону относительно оси S). Соединим все найденные точки плавной кривой и получим диаграмму для определения радиуса исходного контура кулачка.
. Отрезки, значения которых возьмем в миллиметрах, с диаграммы скорости, и отложим их по этим лучам (для фазы удаления в положительную, для фазы сближения в отрицательную сторону относительно оси S). Соединим все найденные точки плавной кривой и получим диаграмму для определения радиуса исходного контура кулачка.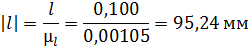
 к оси аналога скорости
к оси аналога скорости  , при пересечении ее с касательной контура кулачка находим точку
, при пересечении ее с касательной контура кулачка находим точку  . Соединив ее с точкой
. Соединив ее с точкой  , получим исходный радиус
, получим исходный радиус  , в данном случае
, в данном случае 
 вспомогательные прямые. От характерных точек отложим перпендикуляры и, замеряя углы, откладываем их на диаграмме углов давления в масштабном коэффициенте угла давления:
вспомогательные прямые. От характерных точек отложим перпендикуляры и, замеряя углы, откладываем их на диаграмме углов давления в масштабном коэффициенте угла давления: .
. поделим на шесть равных дуг и из центра окружности проведем лучи. Радиусами от точки О до 1, 2, 3и так далее по очереди будем проводить дуги до пересечения с лучом, тем самым получим профиль кулачка. Так получим теоретический профиль кулачка.
поделим на шесть равных дуг и из центра окружности проведем лучи. Радиусами от точки О до 1, 2, 3и так далее по очереди будем проводить дуги до пересечения с лучом, тем самым получим профиль кулачка. Так получим теоретический профиль кулачка.
 - начальный радиус, мм.
- начальный радиус, мм.