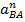|
|
Плоские рычажные механизмыИсходные данные 1. Дано: lOA = 0,14м , lAB = 0,55м , lOC = 0,14м, lСD = 0,40м, lAS2 = 0,18м , lCS4 = 0,13м, α = 45˚, AOC = 90˚, BOD = 90˚, n1=25 мин-1, Pпс = 300Н а) структурный анализ плоского рычажного механизма б) синтез кинематической схемы плоского рычажного механизма 2. Кинематический анализ плоского рычажного механизма а) построение планов положений б) построение планов скоростей и планов ускорений в) определение значений и направлений угловых скоростей и угловых ускорений всех звеньев 3. Силовой анализ плоского рычажного механизма а) составление расчетной схемы б) метод кинетостатики для одного положения кривошипа в) теорема Жуковского для того же положения звеньев 4. Динамический анализ плоского рычажного механизма а) составление динамической модели
б) построение диаграмм в) вывод уравнения и построение диаграммы г) построение диаграммы энергия-масса д) определение значения момента инерции маховой массы
Механизм с высшими кинематическими парами 5. Простой зубчатый механизм
Z2 = 33 M = 1,75
а) структурный анализ простого зубчатого механизма б) синтез эвольвентного зацепления простого зубчатого механизма
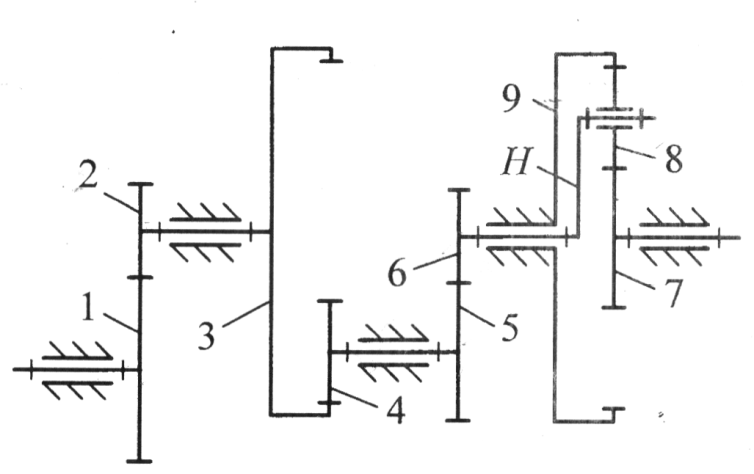
6. а) структурный анализ сложного зубчатого механизма б) синтез кинематической схемы сложного зубчатого механизма в) кинематический анализ сложного зубчатого механизма
I17 = 4,13*10-2, K = 6, m = 5,00мм, α = 20º,
а) структурный и кинематический анализы б) определение радиуса исходного контура в) синтез профилей кулачка
[ϑ]= 45° 8. Завершение работ графической части, оформление пояснительной записки, защита курсового проекта.
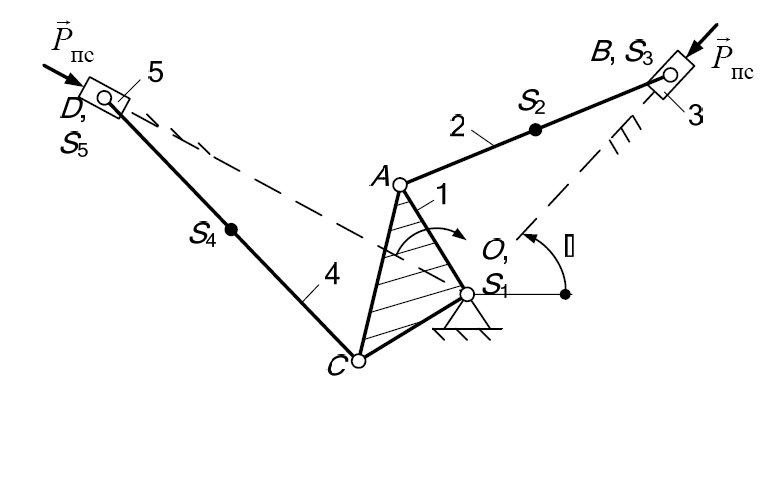
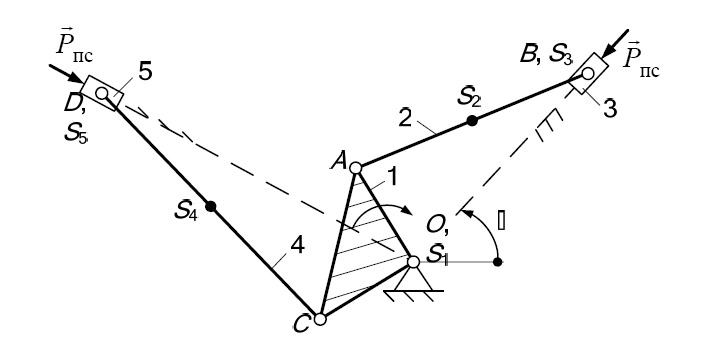
Плоские рычажные механизмы 1.1 Структурный анализ Для данного сложного рычажного механизма необходимо определить число степеней свободы (подвижность) и выполнить структурный анализ. Число степеней свободы исследуемого механизма определим по формуле Чебышева:
где n – число подвижных звеньев в составе исследуемой кинематической цепи;
Для определения величины коэффициента n проанализируем структурную схему механизма . Структурная схема механизма состоит из шести звеньев, рассмотрим движения каждого звена и занесем их в таблицу 1.
Таблица 1 – Звенья механизма.
Звенья 1– 5 являются подвижными звеньями, а стойка 0 – неподвижным звеном. Она представлена в составе структурной схемы двумя направляющими ползуна и шарнирно-неподвижной опорой. Следовательно, n = 5. Для определения коэффициентов и найдем все кинематические пары, входящие в состав рассматриваемой кинематической цепи. Результаты исследований заносим в Таблицу 2 – Кинематические пары.
Таблица 2 – Кинематические пары
Из анализа данных табл. 2 следует, что исследуемый механизм состоит из семи пар пятого класса и образует простая замкнутую кинематическую цепь. Следовательно, Подставив найденные значения коэффициентов n,
Рисунок 2 Группа звеньев 2 – 3 (рисунок 2). Данная группа состоит из двух подвижных звеньев: шатун 2 и ползун 3; двух поводков: кривошип 1 и направляющая (стойка) 0: и трех кинематических пар: 3 – 2 вращательная пара пятого класса; 2 – 1 вращательная пара пятого класса; 3 – 0 поступательная пара пятого класса; тогда
Подставив выявленные значения коэффициентов в формулу Чебышева, получим:
Следовательно, группа звеньев 2-3 является структурной группой 2 класса ( так как число подвижных звеньев n=2), 2 порядка (так как структурная группа имеет 2 поводка), 2 вида (ВВП).
Рисунок 3 Группа звеньев 5 – 4 (рисунок 3). Данная группа состоит из двух подвижных звеньев: шатун 4 и ползун 5; двух поводков: кривошип 1 и направляющая (стойка) 0: и трех кинематических пар: 5 – 4 вращательная пара пятого класса; 4 – 1 вращательная пара пятого класса; 5 – 0 поступательная пара пятого класса; тогда
Подставив выявленные значения коэффициентов в формулу Чебышева, имеем следующий результат:
Следовательно, группа звеньев 5-4 является структурной группой 2 класса (так как число подвижных звеньев n=2), 2 порядка (так как структурная группа имеет 2 поводка), 2 вида (ВВП). Для решения 2-ой задачи структурного анализа плоских рычажных механизмов используется структурная классификация: Рисунок 1 Группа 0-1 состоит из одного подвижного и одного не подвижного звена. Стойка – 0 и кривошип – 1. 0 – 1 – вращательная пара пятого класса; тогда Подставляя найденные значения коэффициентов в формулу Чебышева:
Полученный результат означает, что для однозначного определения возможных положений звеньев данного механизма достаточно одной обобщенной координаты. Следовательно, группа звеньев 0 – 1 не является структурной группой Асура, а представляет собой первичный механизм, подвижность которого равна 1. Из проведённого анализа следует, что подвижность данного сложного рычажного механизма равна 1; механизм имеет следующий структурный состав: первичный механизм с подвижностью равной 1 и две структурные группы 2 класса, 2 порядка, 1 и 2 вида. Структурная формула механизма
Вывод: Из проведенного анализа следует, что подвижность механизма равна 1. Механизм имеет следующий структурный состав: первичный механизм с подвижностью равной 1, и две структурные группы Ассура 2 класса, 2 порядка, 1 и 2 вида. Класс механизма определяется наиболее сложной структурной группой, входящей в его состав, следовательно, данный механизм принадлежит 2 классу.
2 Синтез кинематической схемы плоского рычажного механизма по заданным параметрам Чтобы построить кинематическую схему плоского рычажного механизма по заданным параметрам, нужно найти масштабный коэффициент длины
где
Остальные размеры звеньев вычислим по формуле:
где i – номер звена, для которого вычисляется длина на кинематической схеме.
Перейдем построению положения звеньев механизма относительно друг друга. Для этого на плоскости выбираем точку O. Исходя из задания на курсовой проект находим точку O1. Из точки O1 проводим окружность радиусом |O1B|. Из точки O радиусом
Кинематический анализ 3.1 Построение 12-ти планов положений Построим двенадцать положений механизма в масштабном коэффициенте Процесс построения повторяется до полного завершения построения плана положений, содержащего требуемое число положений ведущего звена. 3.2 Построение планов скоростей относительно 12-ти планов положений для седьмого положения механизма Проанализируем полученную схему механизма: точка О является неподвижной точкой, следовательно, модуль скорости этой точки равен нулю Вектор скорости точки А представляет собой геометрическую сумму вектора скорости точки О и скорости относительного вращательного движения точки А вокруг О:
где
Линия действия вектора Модуль скорости точки А:
где
Зададим масштабный коэффициент скоростей
где
Зададим масштабный коэффициент:
Выбираем в качестве полюса плана скоростей произвольную точку p, проводим в выбранном масштабе вектор Для нахождения скорости точки В рассмотрим вращательное движение второго звена, взяв за полюс точку А. Тогда формула будет иметь следующий вид:
где
С другой стороны точка В вращается вокруг
где
Определим скорость точки E, для этого составим равенство:
Где
Определим скорость точки D, для этого составим векторное уравнение:
В тоже время точка D принадлежит выходному звену, которое совершает возвратно – поступательное движение в вертикальной плоскости вдоль направляющей.
Определим угловые скорости
Направление действия угловой скорости шатуна 2 указывает вектор скорости Направление действия угловой скорости коромысла 3 указывает вектор скорости Строим планы скоростей для оставшихся положений механизма. Вычисляем действительные величины линейных и угловых скоростей для всех положений механизма, округляем полученные значения и сводим их в таблицу 3. Таблица 3 – Угловые и линейные скорости
3.3 Построение планов ускорений относительно 12-ти планов положений для седьмого положения механизма Для построения плана ускорений составим векторные уравнения. Определение ускорений плоского рычажного механизма, также рассмотрим на примере первого положения. Вектор ускорения точки А представляет собой геометрическую сумму вектора ускорения точки О, вектора нормального ускорения и вектора тангенциального ускорения относительного вращательного движения точки А вокруг точки О:
Так как кривошип ОА совершает равномерное вращательное движение
Вектор ускорения Масштабный коэффициент ускорений:
где
Зададим масштабный коэффициент:
Выбираем в качестве полюса плана ускорений произвольную точку p, из точки π в выбранном масштабном коэффициенте проведем вектор Рассмотрим плоское движение второго звена.
где
Ускорение
где
Полное ускорение
Рассчитаем длину вектора
Решим графически векторное равенство и найдём величины Из полюса на плане ускорений, в выбранном масштабе, проведем вектор
Вектор ускорения точки С представляет собой геометрическую сумму вектора ускорения точки О, вектора нормального ускорения и вектора тангенсального ускорения относительного вращательного движения точки С вокруг точки О
Так как кривошип ОС совершает равномерное вращательное движение
Направлено ускорение t wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>C</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> Переведем ускорение точки С в масштабный коэффициент:
Вектор ускорения точки D запишем следующей формулой:
где
Рассчитаем длину вектора
Решим графически векторное равенство и найдём величины Для этого из конца вектора
Найдём угловое ускорение второго звена, зная тангенциальное ускорение
Найдём угловое ускорение четвёртого звена, зная тангенциальное ускорение
Угловая скорость кривошипа 1 является постоянной величиной, следовательно, угловое ускорение этого звена равно нулю, т.е. e1 =0. Ползуны 3 и 5 совершают только поступательные движения, следовательно, угловые ускорение этих звеньев равно нулю, т.е. e3=e5=0. Направление действия углового ускорения шатуна 2 указывает вектор тангенциального ускорения Угловая скорость кривошипа 1 является постоянной величиной, следовательно, угловое ускорение этого звена равно нулю, т.е. e1 =0. Ползуны 3 и 5 совершают только поступательные движения, следовательно, угловые ускорение этих звеньев равно нулю, т.е. e3=e5=0. Направление действия углового ускорения шатуна 4 указывает вектор тангенциального ускорения Строим планы ускорений для оставшихся положений механизма. Вычисляем истинные величины линейных и угловых ускорений для всех положений механизма и сводим их в таблицу 4.
Таблица 4 – Линейные ускорения точек звеньев

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Плоские рычажные механизмы
Плоские рычажные механизмы
 Z1 = 15
Z1 = 15 = 0,42
= 0,42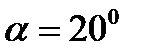
 Сложный зубчатый механизм
Сложный зубчатый механизм
 7. Кулачковый механизм
7. Кулачковый механизм ,
, 
 ,
, 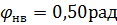
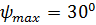 ,
, 
 ,№ сектора - 1
,№ сектора - 1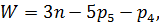
 - число пар четвертого класса;
- число пар четвертого класса; - число пар пятого класса;
- число пар пятого класса;














 , а
, а 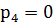 .
. и
и  в формулу Чебышева, получим:
в формулу Чебышева, получим: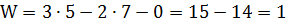
 и
и  .
.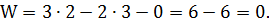
 и
и  .
.
 , который рассчитывается по формуле:
, который рассчитывается по формуле:
 – действительная длина шатуна в метрах;
– действительная длина шатуна в метрах; – размер кривошипа в миллиметрах принимаемый на чертеже.
– размер кривошипа в миллиметрах принимаемый на чертеже.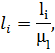
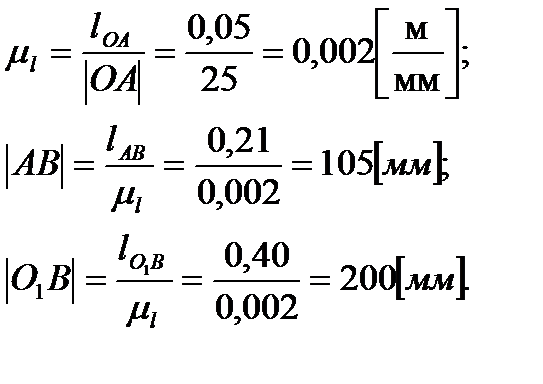
 проводим окружность. Теперь на данной окружности отмечаем точку А, далее откладываем длину шатуна AB из соответствующих точек до пересечения с O1B. В результате чего будут найдены точки B и D. Данное действие проводим для каждого положения.
проводим окружность. Теперь на данной окружности отмечаем точку А, далее откладываем длину шатуна AB из соответствующих точек до пересечения с O1B. В результате чего будут найдены точки B и D. Данное действие проводим для каждого положения. м/мм. Чтобы найти крайние положения, необходимо, отложив длину кривошипа OA и коромысла AB необходимо, чтобы они располагались на одной прямой. Верхнее положение точки D и будет являться нулевым положением м-ма, поскольку движение выходного звена будет совершаться против силы полезного сопротивления. Каждое новое положение механизма получим поворотом кривошипа на 30 градусов в сторону вращения (в данном случае против хода движения часовой стрелки относительно наблюдателя) Второе крайнее положение будет являться таким положением, когда точка D будет максимально приближена к стойке O и после прохождения этой точки начнется холостой ход механизма.
м/мм. Чтобы найти крайние положения, необходимо, отложив длину кривошипа OA и коромысла AB необходимо, чтобы они располагались на одной прямой. Верхнее положение точки D и будет являться нулевым положением м-ма, поскольку движение выходного звена будет совершаться против силы полезного сопротивления. Каждое новое положение механизма получим поворотом кривошипа на 30 градусов в сторону вращения (в данном случае против хода движения часовой стрелки относительно наблюдателя) Второе крайнее положение будет являться таким положением, когда точка D будет максимально приближена к стойке O и после прохождения этой точки начнется холостой ход механизма. .
.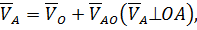
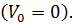
 – вектор скорости точки А;
– вектор скорости точки А; – вектор скорости точки О, принятой за полюс;
– вектор скорости точки О, принятой за полюс; – вектор скорости вращения точки А вокруг точки О.
– вектор скорости вращения точки А вокруг точки О.
 – угловая скорость звена AO,
– угловая скорость звена AO,  ;
; – длинна звена АO, м;
– длинна звена АO, м; 
 – частота вращения звена АO,
– частота вращения звена АO, 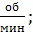
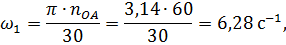
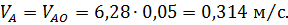
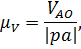
 – значение скорости вращения точки А вокруг точки О;
– значение скорости вращения точки А вокруг точки О; – длина отрезка
– длина отрезка  на плане скоростей, представляющая скорость
на плане скоростей, представляющая скорость 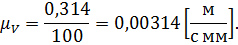
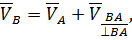
 – вектор неизвестной скорости точки В.
– вектор неизвестной скорости точки В. – вектор скорости точки В при её вращении вокруг точки А.
– вектор скорости точки В при её вращении вокруг точки А. . Следовательно, скорость точки В можно представить следующей формулой:
. Следовательно, скорость точки В можно представить следующей формулой: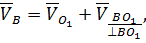
 .
.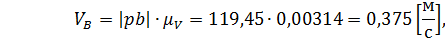
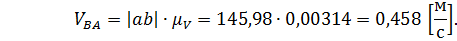
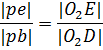
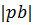 - длина вектора скорости точки B на плане скоростей,
- длина вектора скорости точки B на плане скоростей, - неизвестная длина вектора скорости точки E на плане скоростей (оба вектора имеют общий полюс и сонаправлены, поскольку обе точки принадлежат одному и тому же звену)
- неизвестная длина вектора скорости точки E на плане скоростей (оба вектора имеют общий полюс и сонаправлены, поскольку обе точки принадлежат одному и тому же звену) ,
,  - длины отрезков на плане положений механизма.
- длины отрезков на плане положений механизма.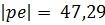
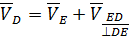
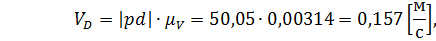
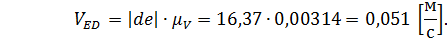
 ,
,  и
и  звеньев 2, 3 и 4. Величины этих скоростей определяются из равенств:
звеньев 2, 3 и 4. Величины этих скоростей определяются из равенств: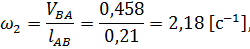
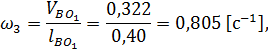
 (т.к. звенья 3 и 5 являются ползунами, совершающими только поступательное движение).
(т.к. звенья 3 и 5 являются ползунами, совершающими только поступательное движение). , перенесенный с плана скоростей в точку В на схему механизма. Точка А условно делается неподвижной. Соответственно при данном условии разрывается связь. В этом случае точка В совместно с шатуном 2 под действием вектора
, перенесенный с плана скоростей в точку В на схему механизма. Точка А условно делается неподвижной. Соответственно при данном условии разрывается связь. В этом случае точка В совместно с шатуном 2 под действием вектора  , перенесенный с плана скоростей в точку B на схему механизма. Полученное направление вращательного движения коромысла 3 будет являться направлением действия угловой скорости данного звена.
, перенесенный с плана скоростей в точку B на схему механизма. Полученное направление вращательного движения коромысла 3 будет являться направлением действия угловой скорости данного звена.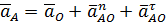
 , то точка А рассматриваемого механизма будет иметь только нормальное ускорение, равное по величине:
, то точка А рассматриваемого механизма будет иметь только нормальное ускорение, равное по величине: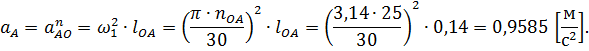
 направлен к оси вращения О.
направлен к оси вращения О.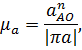
 – действительное значение нормального ускорения точки А, при вращении вокруг точки О;
– действительное значение нормального ускорения точки А, при вращении вокруг точки О; – длина отрезка
– длина отрезка  на плане ускорений, представляющая ускорение
на плане ускорений, представляющая ускорение  на плане ускорений.
на плане ускорений.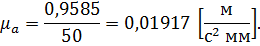
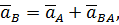
 – вектор ускорения точки В;
– вектор ускорения точки В; – вектор ускорения точки А;
– вектор ускорения точки А; –вектор ускорения точки В при её вращении вокруг точки А.
–вектор ускорения точки В при её вращении вокруг точки А. можно представить в виде:
можно представить в виде: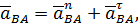
 – вектор нормального ускорения точки В при её вращении вокруг точки А и равное:
– вектор нормального ускорения точки В при её вращении вокруг точки А и равное: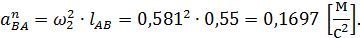
 – вектор тангенциального ускорения точки В при её вращении вокруг точки А, направленное перпендикулярно радиусу вращения АВ и равное:
– вектор тангенциального ускорения точки В при её вращении вокруг точки А, направленное перпендикулярно радиусу вращения АВ и равное: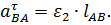
 можно записать в следующем виде:
можно записать в следующем виде: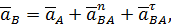
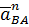 на плане ускорений:
на плане ускорений: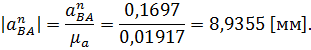
 .
.

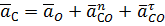
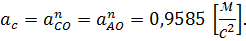
 к оси вращения О.
к оси вращения О.
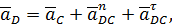
 – вектор ускорения точки D;
– вектор ускорения точки D; – вектор ускорения точки C;
– вектор ускорения точки C; – вектор нормального ускорение точки D при её вращении вокруг точки C и равное:
– вектор нормального ускорение точки D при её вращении вокруг точки C и равное:
 – вектор тангенциального ускорение точки D при её вращении вокруг точки C, направленное перпендикулярно радиусу вращения CD и равное:
– вектор тангенциального ускорение точки D при её вращении вокруг точки C, направленное перпендикулярно радиусу вращения CD и равное:

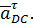
 и
и  и умножив их на масштабный коэффициент ускорений, в котором строиться план ускорений, получим истинные значения
и умножив их на масштабный коэффициент ускорений, в котором строиться план ускорений, получим истинные значения 

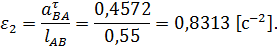
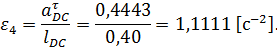
 , перенесенный с плана ускорений в точку В на схему механизма. Точку А считаем условно неподвижной. При этом условии, соответственно, разрывается связь между кривошипом 1, ползуном 3 и шатуном 2. В этом случае точка В совместно шатуном 2 под действием вектора
, перенесенный с плана ускорений в точку В на схему механизма. Точку А считаем условно неподвижной. При этом условии, соответственно, разрывается связь между кривошипом 1, ползуном 3 и шатуном 2. В этом случае точка В совместно шатуном 2 под действием вектора 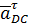 , перенесенный с плана ускорений в точку D на схеме механизма. Точку С делаем условно неподвижной. При этом разрывается связь между кривошипом 1, ползуном 5 и шатуном 4. В этом случае точка Dсовместно шатуном 4 под действием вектора
, перенесенный с плана ускорений в точку D на схеме механизма. Точку С делаем условно неподвижной. При этом разрывается связь между кривошипом 1, ползуном 5 и шатуном 4. В этом случае точка Dсовместно шатуном 4 под действием вектора