Метод наибольшего правдоподобия

Случай непрерывных распределений

Пусть x , x … x – независимая выборка из непрерывного распределения с плотностью p(x; θ).

Определение 1: Функция вида L(x , x … x ; θ)=p(x ; θ)…p(x ; θ) называется функцией правдоподобия.

Определение 2: Оценкой наибольшего правдоподобия параметра θ называют число , которое находится из условия L(x , x … x ; )=max L(x , x … x ; θ)

При выполнении некоторых условий, смысл которых состоит в том, что p(x; θ) – достаточно гладкая функция, а интеграл =1 достаточно быстро сходится, оценка максимального правдоподобия обладает следующими свойствами:

1. она состоятельна

2. она асимптотически нормальна, т.е при больших n можно рпиближенно считать, распределение приближенно нормельным.

3. она асимптотически эффективна, т.е при больших n оценку можно считать близкой к эффективной.

Недостатком метода является то, что иногда оценки получаются смещенными.

Случай дискретного распределения

Определение 1: Пусть P( )=P , где – число из выборки, а – та случайная величина, которая приняла значение . Функция вида L(x , x … x ; θ)=P(x ; θ)…P(x ; θ) называется функцией правдоподобия в дискретном случае.

Оценкой наибольшего правдоподобия параметра θ называют число , которое находится из условия L(x , x … x ; )=max L(x , x … x ; θ).

Пример: Методом наибольшего правдоподобия найти оценку параметра λ распределения Пуассона P = , λ>0, – целые неотрицательные числа.

Решение. Составляем функцию правдоподобия L(x , x … x ; λ)=

И находим, что ее максимум достигается в точке = .

25.Интервальнойназывают оценку, которая определяется двумя числами – концами интервала, покрывающего оцениваемый параметр.

Доверительным называют интервал, который с заданной надёжностью γ покрывает заданный параметр.

Интервальной оценкой (с надёжностью γ) математического ожидания а нормального распределённого количественного признака по выборочной средней х_в

1. при известном среднем квадратическом отклонении σ генеральной совокупности служит доверительный интервал х_в – t (σ/√n) < a < х_в + t (σ/√n), где δ = t (σ/√n) – точность оценки, n – объём выборки, t – значение аргумента функции Лапласа Ф(t), при котором Ф(t) = γ/2.

2. при неизвестном σ (и объёме выборки n < 30) х_в – t_γ (s/√n) < a < х_в + t_γ (s/√n), где s – исправленное выборочное среднее квадратическое отклонение, t_γнаходят по таблицам распределения Стьюдента по заданным n (число степеней свободы k = n – 1) и γ.

Интервальной оценкой (с надёжностью γ) среднего квадратического отклонения σ нормально распределённого количественного признака Х по исправленному выборочному среднему квадратическому отклонению s служит доверительный интервал s (1 – q) < σ < s (1 + q) (при q < 1), 0 < σ < s (1 + q) (при q > 1), где q находят по таблицам распределения χ² по заданным n и γ.

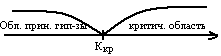
26.Общая схема проверки гипотез:

1) выдвигается основная гипотеза Н₀ и альтернативнаяН_1; выбирается α

2) выбирается статистика К, с помощью кот-ой будет проверяться выдвинутая гипотеза

3) Вся область возможных значений статистики к разбивается на 2 непересекающиеся области: критическую и область принятия гипотезы, разделённые критическими точками

4) По имеющейся выборке выч-ся значение статистики К_набл и определяют, в какую из 2-х областей оно попадает, и на основании этого принимается решение относит-но истинности Н₀

Критическими точками (границами) k_кр называют точки, отделяющие критическую область от области принятия гипотезы.

Правосторонней называют критическую область, определяемую неравенством К > k_кр, где k_кр – положительное число.

Левосторонней называют критическую область, определяемую неравенством К < k_кр, где k_кр – отрицательное число.

Двусторонней называют критическую область, определяемую неравенством К < k₁, K > k₂, где k₂ > k₁.

В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется область определяется неравенствами (в предположении, что k_кр > 0) К < – k_кр, K > k_кр, или равносильным неравенством: | K | > k_кр.

Опр. Область допустимых значений – совокуп-ть значений критерия К, на основании кот-ых принимается основная гипотеза. К–случ.вел-на

Не нашли, что искали? Воспользуйтесь поиском по сайту: