
|
|
Закон распределения и функц. распред. дискретной случ. величиныГеометрическая вероятность. Постановка задачи: пусть G – огранич. плоская область с конечной площадью. В эт. области содержится обл. g облад-щая те-ми же св-ми. В обл. G наугад бросается точка, она может попасть в любое место обл-ти G (рис.1). Вер-ть точки попасть в g пропорциональна отношению площадей G и g и не зависит от ее формы и расположения. Т.о. вер-ть попадан. в обл. g точки, брош. в обл. G наудачу, =, по опред.: Р=S(g)/S(G), S(g) и S(G) – площ. g и G в общем виде S(g) и S(G) – меры множеств g и G. Задача о встрече: Два лица А и В условились встретиться м/у 12 и часом дня. Пришедший первым ждёт 20 минут и уходит. Какова вероятность встречи, если приход каждого в течен. часа мож. произойти наудачу и моменты прихода А и В независимы. Решение: обозначим момент прихода А через х, а В – у. Изобразим х и у как декарт. коорд-ты, единиц. масшт. – 1 мин. (рис.2). Всевозможн. исходы можн. изобразить ввиде пар (х, у) – т. квадрата со стороной 60. Встр. состоится, если ½x – y½ ≤20 (заштрих. обл.). Область G =60 2, g = 60 2 - 2*0,5*(40*40) = 602- 402, p = (602- 402) / 602= 5 / 9.
4.Теоремы сложения и умножения вер-тей Теорема сложения вер-тей: Вер-ть суммы 2-х совместных соб-ий = вер-ти суммы этих событий минус вер-ть их пересечений АВ Док-во: А+В=А А Выразим через А,В,АВ: А= А B=B Р(А)=Р(А Р(В)= B Р(B P(А подставляем в Р(А+В): Р(А+В)= P(A)–P(AB)+P(B)–P(AB)+Р(АВ)= P(A)–P(AB)+P(B). Теорема доказана Теорема умножения вероятностей: Вер-ть совместного появления двух событий равна произведению вер-ти одного из них на условную вер-ть другого, вычисленную в предположении, что первое событие уже наступило:P(AB) = P(A) ∙ PA(B).Для независимых событий:P(AB) = P(A) ∙ P(B), т.е. вер-ть совместного появления двух независимых событий равна произведению вер-тей этих событий.
5. Формула полной вероятности:Вер-ть события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) В1, В2, … , Вn, образующих полную группу, равна сумме произведений вер-тей каждой из гипотез на соответствующую условную вер-ть события А:P(A) = P(B1) ∙ PB1(A) + P(B2) ∙ PB2(A) + … + P(Bn) ∙ PBn(A), где P(B1) + P(B2) + … + P(Bn) = 1. Формула Бейеса:Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) В1, В2, … , Вn, которые образуют полную группу событий. Если событие А уже произошло, то вер-ти гипотез могут быть переоценены по формулам Бейеса: PA(Bi) = P(Bi) ∙ PB1(A) / P(A) (i = 1, 2, … , n), где P(A) = P(B1) ∙ PB1(A) + P(B2) ∙ PB2(A) + … + P(Bn) ∙ PBn(A).
6. Формула Бернулли: Pn(m) = Cmnpmqn–m, где n – число опытов в одинаковых условиях, m – число опытов, в которых произошло событие А, р – вероятность события А при каждом испытании, q = 1 – p. Функция распределения: F(x) = P(X < x) = ∑ xi<x p(xi).
Закон распределения и функц. распред. дискретной случ. величины Опр.5. Любое правило (таблица ф-ий и т.д.), позволяющее находить вер-ть всех возможных событий, связанных со случайной величиной, наз-ся законом распределения случ. вел-ны. Опр.6. 2 случайные вел-ны наз-ся независимыми, если зак-н распределения одной их них не зависит от того, как распределена другая. В противоположном случае говорят, что они зависимы. Для дискретной случ. вел-ны рядомраспределения наз-ся закон распределения этой вел-на в виде таблицы. В верхней части расположены все значения, кот-ые м. принимать случ-я вел-на (в порядке возрастания), а в нижней – соответсвующая им вероятность.
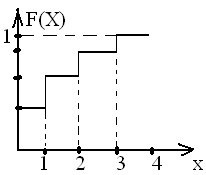
Pi=P{X=xi} События несовместны и образуют полную группу несовм-х соб-ий. Опр.7 Функцией распределения случ. вел-ны Х наз-ся вер-ть того, что случ. вел-на Х примет значение меньшее заданного F(X)=P{X<x}, Свойства ф-ии распределения 1) Ф-ия распределения F(X) неубывающая для ф-ии своего аргумента (т.е. для любых х1, х2: х1<х2 F(x1) Док-во: возьмём 2 произвольные точки х1и х2:
P(C)=P(A+B)=P(A)+P(B) F(x2)= F(x1)+P{x1 2) Значение ф-ии распределения стремится к 0 при х–> –
3)Функция распределения непрерывна слева.
Значение ф-ии распределения для случ. вел-ны:
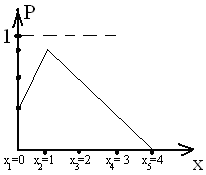
Графический ряд распределения изображается в виде ломаной, кот-я наз-ся многоугольником распределения.
8.Математических ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности: M(x) = ∑ni=1 xi∙pi = х1р1 + х2р2 + … + хnpn.Если дискретная случайная величина принимает счётное множество возможных значений, то математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическое ожидание обладает следующими свойствами. Свойство 1. Математическое ожидание постоянной величины равна самой постоянной: М(С) = С. Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = С∙М(Х). Свойство 3. Математическое ожидание произведения взаимно независимых случайных величин равно произведению математических ожиданий сомножителей: М(Х1Х2…Хn) = M(X1)∙M(X2)∙…∙M(Xn). Свойство 4. Математическое ожидание суммы случайных величин равно сумме математических ожиданий слагаемых: М(Х1+Х2+…+Хn) = M(X1) + M(X2) +…+ M(Xn). Характеристиками рассеяния возможных значений случайной величины вокруг математического ожидания служат, в частности, дисперсия и среднее квадратическое отклонение. Опр.9. Дисперсией случайной величины Х называют математическое ожидание квадрата отклонения случайной величины от её математического ожидания: D(x) = ∑ni=1 (xi – M(x))2pi = M(x2) - M2(x). Дисперсия обладает следующими свойствами. Свойство 1. Дисперсия постоянной равна нулю: D(С) = 0. Свойство 2. Постоянный множитель можно выносить за знак дисперсии, предварительно возведя его в квадрат: D(С∙Х) = С2∙D(Х). Свойство 3. Дисперсия суммы независимых случайных величин равна сумме дисперсий слагаемых: D(Х1+Х2+…+Хn) = D(X1) + D(X2) +…+ D(Xn).
Непрерывные случ. вел-ны Опр.1 Случ. вел-на Х наз-ся непрерывной, если её ф-ия распределения F(X) непрерывна в любой точке числовой прямой и диф-ма всюду, кроме, быть может, отдельных точек, где она терпит излом. Опр.2. Плотностью распределения вероятностей непрерывной случайной величины называют первую производную от функции распределения: f(x) = F'(x). Свойства: Свойство 1. Плотность распределения неотрицательна, т.е. f(x) ≥ 0. (как производная неубывающей ф-ии распределения) Свойство 2. Вер-ть попадания непрер-ой случ. вел-ны в Док-во: Свойство 3. Ф-ия распределения непрер-ой случ. вел-ны равна F(x) = ∫х–∞ f(x)∙dx. Док-во: F(X)=P{X<x}=P{– Свойство 4. Несобственный интеграл от плотности распределения в пределах от -∞ до +∞ равен единице: ∫+∞-∞ f(x)∙dx = 1. Док-во: рассм-м
10.Математическое ожидание непрерывной случайной величиныХ, возможные значения которой принадлежат всей оси Ох, определяется равенством: M(x) = ∫+∞-∞ x∙f(x)∙dx, где f(x) – плотность распределения случайной величины Х. Предполагается, что интеграл сходится абсолютно. Все свойства математического ожидания, указанные для дискретных случайных величин, сохраняются и для непрерывных величин. Опр.4. Дисперсия непрерывной случайной величины Х, возможные значения которой принадлежат всей оси Ох, определяется равенством: D(x) = ∫+∞-∞ [x – M(x)]2∙f(x)∙dx, или равносильным равенством: D(x) = ∫+∞-∞ x2∙f(x)∙dx – [M(x)]2. Все свойства дисперсии, указанные для дискретных случайных величин, сохраняются и для непрерывных величин.
11. Опр.5. Среднее квадратическое отклонение непрерывной случайной величины определяется так же, как и для дискретной величины: σ(х) = √D(x). Опр.6. Модой М0(Х) непрерывной случайной величины Х называют то её возможное значение, которому соответствует локальный максимум плотности распределения. В частности, если распределение имеет два одинаковых максимума, то его называют бимодальным. Опр.7. Квантиль порядка р есть точка (число) хр такая, что вероятность попадания случайной величины левее этой точки, равна р: Р(Х < xp) = p. Квантиль порядка 1/2 называется медианой. Опр.8. Медианой Ме(Х) непрерывной случайной величины Х называют то её возможное значение, которое определяется равенством: Р[X < Ме(Х)] = P [ X > Ме(Х)]. Геометрически медиану можно истолковать как точку, в которой ордината f(x) делит пополам площадь, ограниченную кривой распределения.
12. Начальный теоретический момент порядка k непрерывной случайной величины Х определяется равенством: νk = ∫+∞-∞ xk∙f(x)∙dx. Опр.10. Центральный теоретический момент порядка k непрерывной случайной величины Х определяется равенством: µk = ∫+∞-∞ [x – M(x)]k∙f(x)∙dx. Центральные моменты выражаются через начальные моменты по формулам: μ2 = ν 2 – ν 21, μ3 = ν 3 – 3 ν 1 ν 2 + 2 ν 31, μ4 = ν 4 – 4 ν 1 ν 3 + 6 ν 21 ν 2 – 3 ν 41.
13.Биномиальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна р; вероятность возможного значения Х = k (числа k появлений события) вычисляются по формуле Бернулли: Pn(k) = Ckn pk qn-k. Или другими словами: при повторении n одинаковых независимых опытов некоторое событие А может случиться k раз. Если каждый раз вероятность результата А есть р, то случайная величина имеет биномиальное распределение. Опр.3. Математическое ожиданиебиномиального распределения равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np. Опр.4. Дисперсия биномиального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.
14Биномиальный закон распред Если число испытаний велико (n >> 1), а вероятность р появления события в каждом испытании очень мала (p << 1), то используют приближённую формулу: Pn(k) = λk e-λ / k!, где k – число появлений события в n независимых испытаниях, λ = np (среднее число появлений события в n испытаниях), и говорят, что случайная величина распределена по закону Пуассона. Опр.6. Математическое ожидание распределения Пуассона равно произведению числа испытаний на вероятность появления события в одном испытании: M(X) = np = λ. Опр.7. Дисперсия распределения Пуассона равна произведению числа испытаний на вероятность появления события в одном испытании, то есть равнаматематическому ожиданию: D(X) = np = λ. Теорема Пуассона: Если число опытов n велико, а вер-ть успеха в отдельном опыте р мала (0<p<1) и произведение np= λ = const, то ф-лу Пуассона с параметром λ =.np м приблизительно применять вместо ф-лы Бернулли: Pn(m) = Cmnpmqn–m Замечание: использование ф-лы Пуассона как предельной для ф-лы Бернулли оправдывает себя при npq

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

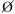 => P(A+B)=P(A)+P(B)-P(AB)
=> P(A+B)=P(A)+P(B)-P(AB) +AB+B
+AB+B 
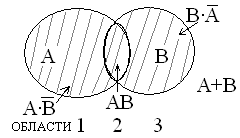 – попарно несовместны => Р(А+В)=Р(А
– попарно несовместны => Р(А+В)=Р(А 











 F(x2))
F(x2)) Пусть С={X<x2}. А={X<x1}. B={x1
Пусть С={X<x2}. А={X<x1}. B={x1  0 по опред-ю вер-ти
0 по опред-ю вер-ти и предел ф-ии распределения = 1.
и предел ф-ии распределения = 1.




 равна
равна 
 . Но т.к ф-я распред-я явл-ся первообразной для плотности (по опред.), то по ф-ле Ньютона-Лейбница, приращ-е первообразной на отрезке – это и есть опред-ый интеграл.
. Но т.к ф-я распред-я явл-ся первообразной для плотности (по опред.), то по ф-ле Ньютона-Лейбница, приращ-е первообразной на отрезке – это и есть опред-ый интеграл.

 причём k=0,1,…n,..
причём k=0,1,…n,..