
|
|
Показательный закон распределения
Функция распределения показательного закона: F(x) = 0 при х < 0 и F(x) = 1 – exp( – λ∙x) при х ≥ 0. Вероятность попадания в интервал (a, b) непрерывной случайной величины Х, распределённой по показательному закону, P(a < Х < b) = exp( – λ∙a) – exp( – λ∙b). Математическое ожидание, дисперсия и среднее квадратическое отклонение показательного распределения соответственно равны: M(X) = 1/ λ, D(X) = 1/ λ2, σ(X) = 1/λ.
16 Нормальное распределение (гауссово распр-е): возникает тогда, когда на параметры случ-ой вел-ны влияют факторы, в сумме кот-рые изменяют параметры Х, но со временем всё вернётся и станет нормальным
Теорема 1: MXN=m Теорема 2: DXN=σ 2 Опр.2 Нормальное распределение с параметром N(0,1) наз-ся стандартным нормальным распределением.
Вероятность попадания случайной величины между точками a и b для нормального распределения:
Свойства ф-ии Лапласа: 1)Ф(-х)= –Ф(х) => нечётная; 2)
18. Локальная теорема Муавра-Лапласа: Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < p < 1), событие наступит ровно k раз (безразлично в какой последовательности), приближённо равна (тем точнее, тем больше n): Pn(k) = 1/ φ(x) – плотность нормального распределения. 1) npq>9 2) φ(x) – по таблице В случае, когда p Интегральная теорема Муавра-Лапласа:Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < p < 1), событие наступит не менее k1 раз и не более k2 раз, приближённо равна: P(k1; k2) = Ф(x'') – Ф(x'). Здесь: Ф(x) = 1/√2π ∙ ∫х0 exp( – t2/2 ) dt – функция Лапласа, x'' = (k2 – np) /
19.Неравенство Чебышева:Если случайная величина имеет конечную дисперсию, то для любого положительного числа Или в другой форме: P(|X – M(X)| ,< Теорема Чебышева:Если последовательность независимых случайных величин Х1, Х2, Х3, … Хn имеет конечные дисперсии, ограниченные одной и той же постоянной: D(Xi) < C, тогда для любого положительного числа Док-во: Утвер: Для независимых случ. вел-н дисперсия их суммы равна сумме их дисперсий. Тогда
20. Вариационный ряд – список вариант строго в порядке их возрастания. Например: 1,2,5,7,8. Статистическим рядом распределения называется таблица, аналог закона распределения дискретной величины с заменой вероятности на относительную частоту.
Здесь n – объём выборки, xi – выборочные значения соответствующего параметра. Эмпирическая функция распределения: F*(x) = nx/n, где nx – число вариант, меньших х, n – объём выборки
Опр.12. Полигоном частот (относит-ых) наз-ся график, в кот-ом по горизонтали отложены значения вариант, а по вертикале – относит-ой частоты, и точки пересечения соединятся ломаной.
21 Выборочное среднее Опр.14. Генеральная средняя – средняя арифметическая вариант дискретной генеральной совок-ти N. P{X=xi}=1/N Генеральная средняя равна матем. ожиданию Опр.15. Выборочной дисперсией наз-ся среднее арифметич. Квадратов отношений вел-ны от их среднего значения Опр.16. Выборочным средним квадратичным отклонением называют квадратный корень из выборочной дисперсии: Опр.17.Модой выборки наз-ся вариант с наибольшей частотой Опр.18. Медианой выборки наз-ся её серединное значение. Если объём выборки нечётный, то медиана – серединное значение. Если объём чётный, то берётся среднее арифметическое значение 2-х центральных вариант.
Основные понятия теории оценок Опр.1. Любая ф-ия от выборки (числовая) наз-ся статистикой.
Задача оценки параметра а состоит в том, чтобы подобрать статистику Опр.2. Если с ростом объёма выборки n оценка Опр.3. Оценка нас волнует такая, что её матем. ожидание равно оцениваемому параметру, наз-ся несмещённой. Если это не так, то оценка смещённая. Теор. (о состоя-ти оценки): Если оценка Док-во: Воспользуемся нер-вом Чебышева: Опр.4. Несмещённая оценка параметра а наз-ся эффективной, если её дисперсия наименьшая по сравнения с дисперсией любой другой несмещённой оценки. Опр.5. Оценку наз-ют точечной ,если она определяется одним числом. Оценка вер-ти случайного события А Проведём серию из n независимых опытов Х – число появления события А в этих опытах По теореме Бернулли, возьмём в качестве оценки относит-ую частоту Теорема: Оценка
22. Статистическая оценка – любая функция от выборки. Свойства статистической оценки: 1. Несмещенность 2. Состоятельность 3. Эффективность Теорема: Оценки Доказательство: Сначала докажем несмещенность оценок. Нужно проверить, что M По определению имеем
Далее, M Выполним тождественные преобразования:
Далее воспользуемся тем, что MX
Докажем состоятельность оценки D Если D

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
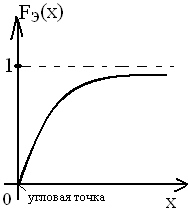
 Опр.3.Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью: f(x) = 0 при х < 0 и f(x) = λ∙exp( – λ∙x) при х ≥ 0, где λ – постоянная положительная величина.
Опр.3.Показательным (экспоненциальным) называют распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью: f(x) = 0 при х < 0 и f(x) = λ∙exp( – λ∙x) при х ≥ 0, где λ – постоянная положительная величина.
 Опр.1. Случайная вел-на Х распределена нормально с математическим ожиданием m и средним квадратическим отклонением σ: f(x) = 1/σ
Опр.1. Случайная вел-на Х распределена нормально с математическим ожиданием m и средним квадратическим отклонением σ: f(x) = 1/σ  ∙
∙ 

 Т.о. случ-я вел-на z имеет станд. нормалное распределение
Т.о. случ-я вел-на z имеет станд. нормалное распределение
 — функция Лапласа
— функция Лапласа ; 3)
; 3)  ; 4) x
; 4) x  5 => Ф(х)
5 => Ф(х)  1/2
1/2 ∙ φ(x). Здесь:φ(x) = 1/√2π ∙ exp( –x2/2 ), x = (k – np) /
∙ φ(x). Здесь:φ(x) = 1/√2π ∙ exp( –x2/2 ), x = (k – np) / 
 q
q  : P(|X – M(X)| ≥
: P(|X – M(X)| ≥  ) < D(X)/
) < D(X)/  .
. ,
, справедливо рав-во: lim n→∞ Р( | 1/n ∑ni=1 Xi – M(X) | <
справедливо рав-во: lim n→∞ Р( | 1/n ∑ni=1 Xi – M(X) | <  ) = 1.
) = 1. ,
,  ,
,  ,
, 
 Опр.11. Гистограммой частот (относит-ых) наз-ют ступенчатую фигуру, состоящую из прямоугольников, основанием кот-ых служит интервал длины h, а высоты равны
Опр.11. Гистограммой частот (относит-ых) наз-ют ступенчатую фигуру, состоящую из прямоугольников, основанием кот-ых служит интервал длины h, а высоты равны 
 наз-ся средняя арифметическая значений вариант выборки
наз-ся средняя арифметическая значений вариант выборки 



 —статистика
—статистика

 , кот-я в некотором смысле была бы близка к оцениваемому параметру
, кот-я в некотором смысле была бы близка к оцениваемому параметру сколь угодно близко приближается к оцениваемым параметрам а, то такая оценка наз-ся состоятельной
сколь угодно близко приближается к оцениваемым параметрам а, то такая оценка наз-ся состоятельной 

 — несмещённая оценка.
— несмещённая оценка. , то такая оценка будет состоятельной.
, то такая оценка будет состоятельной. . Возьмём произвольное
. Возьмём произвольное  .
.  . Перейдём к пределам:
. Перейдём к пределам:  . С вероятностью 1 будет противоположное нер-во. Теорема док-на
. С вероятностью 1 будет противоположное нер-во. Теорема док-на
 — индикатор события А.
— индикатор события А.  — число успехов
— число успехов
 ,равная относит. частоте
,равная относит. частоте  = x / n явл-ся состоятельной, несмещённой и эффективной.
= x / n явл-ся состоятельной, несмещённой и эффективной. и
и  – несмещенные, а оценка
– несмещенные, а оценка  – состоятельная.
– состоятельная. .
. M
M  =
=  =a.
=a. , где
, где 
 =
=  =
=  =
= 

 = σ
= σ  M (X
M (X  X
X  )=MX
)=MX  ( случайные величины X
( случайные величины X  =
=  σ
σ  =(1–
=(1–  ) σ
) σ 
 → 0.
→ 0.