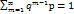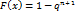|
|
Свойства плотности распределения1. Плотность распределения — неотрицательная функция f(x)>=0. 2.2. Несобственный интеграл от плотности распределения в пределах от -∞ до равен единице: Условие нормировки: Геометрически основные свойства плотности f(x) интерпретируются так: - вся кривая распределения лежит не ниже оси абсцисс; - полная площадь, ограниченная кривой распределения и осью абсцисс, равна единице.
Числовые характеристики случайных величин. Мат ожидание. Свойства мат ожидания. Математическое ожидание дискретной случайной величины есть сумма произведений всех её возможных значений на их вероятности: Свойства математического ожидания.
Числовые характеристики случайных величин. Дисперсия. Свойства. Среднее квадратное отклонение Дисперсия дискретной случайной величины есть математическое ожидание квадрата отклонения случайной величины от её математического ожидания: Свойства дисперсии. Среднее квадратическое отклонение дискретной случайной величины, оно же стандартное отклонение или среднее квадратичное отклонение есть корень квадратный из дисперсии:
Числовые характеристики случайных величин. Квантили. Мода, медиана. Начальные и центральные моменты. Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность. На многоугольнике распределения мода - это абсцисса самой высокой точки. Бывает, что распределение имеет не одну моду. Начальным моментом порядка kслучайной величины Х называется матема-тическое ожидание величиныXk: νk = M (Xk). В частности, ν1 = М(Х), ν2 = М(Х2). Следовательно, дисперсия D(X) = ν2 — ν1². Центральным моментом порядка kслучайной величины Х называется мате-матическое ожидание величины (Х — М(Х))k: μk = M((Х — М(Х))k) Медианой Ме непрерывной случайной величины называют такое ее значение, для которого p( X < Me ) = p( X > Me ). Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части. Для случайной величины Х с функцией распределения F(X) квантилью порядка р (0 < p < 1) называется число Кр такое, что F(Kp) ≤ p, F(Kp + 0) ≥ p. В частности, если F(X) строго монотонна, Кр: F(Kp) = p.
Производящая функция (случай целочисленных случайных величин). Это частный случай Хар.функции.
Свойства. Если Х=m(целые числа), то Z=
Биноминальный закон распределения. Это распределение вероятностей возможных чисел появления события А при n независимых испытаниях, в каждом из которых событие А может осуществиться с одной и той же вероятностью Р(А)=р=const. Кроме события А может произойти также противоположное событие, вероятность которого Р(А)=1-p=q. Вероятности любого числа событий соответствуют членам разложения бинома Ньютона:
Числовые характеристики Бин. распределения: М(m)=np ; D(m)=npq; Ϭ(m)=
Закон распределения Пуассона. Это распределение дискретного типа, моделирует случайную величину, представляющую собой число событий, произошедших за фиксированное время, при условии, что данные события происходят с некоторой частотой и независимо друг от друга. Р(м)=р(Х=м)=(ам/м!)*е-а Условие нормировки: Геометрический закон распределения Это распределение дискретной случайной величины равной количеству испытаний до первого успеха. Р(Х=м)=qм-1р; Mx=q/p; Dx=q/p2 Условие нормировки: Ф. распределения:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
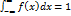





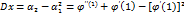
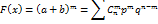
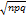
 =1
=1