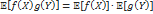|
|
Вероятностное пространство.Конечное вероятностное пространство. Пусть эксперимент имеет конечное число возможных исходов: Ω = {ω1,ω2,…, ωn} – Пространство элементарных событий. S (сигма- алгебра) 1. 2. Состоит из всех подмножеств множества 𝛺. Всего таких подмножеств: Все подмножества можем подсчитать с помощью суммы биномиальных коэффициентов. Каждое случайное событие можно выразить через множество каких-то элементарных исходов. Поставим в соответствие каждому элементарному исходу некоторое число – вероятность элементарного события:
1. Неотрицательности: p(ωi) ≥ ,0 ∀ωi ∈Ω 2. Нормированности: Тогда вероятностью события А будет число р(А):
Если для каждого элементарного исхода определить вероятность, то вероятность случайного события, состоящего из этих элементарных исходов, будет равна сумме вероятностей соответствующих элементарных исходов.
1.9Условная вероятность. Пусть случайные события, причём . Замечания
Прямо из определения очевидно следует, что вероятность произведения двух событий равна:
Если · Условная вероятность является вероятностью, то есть функция,
Пример Если A, B — несовместимые события, то есть
Предположим, что по статистике вероятность того, что человек доживает до 80 лет Какова вероятность того, что человек доживший до 80 лет доживет до 90?
1.10 вероятность произведения события Р(А В) = Р(А)PA(В) . Так как для вычисления вероятности произведения не играет роли какое из рассмотренных событий А и В было первым, а какое вторым, то можно записать: Р(А В) = Р(А) PA(В) = Р(В) PB(А). Теорема умножения вероятностей для независимых событий. Вероятность произведения двух независимых событий равна произведению вероятности этих событий: Р(АВ) = Р(А) P(В).
1.11 Независимость событий. Вероятность появления события A не меняет вероятности события B. Определение 2. Пусть есть семейство (конечное или бесконечное) случайных событий
пределение 3. Пусть есть семейство (конечное или бесконечное) случайных событий
Независимые сигма-алгебры[ Определение 4. Пусть A1, A2
Независимые случайные величины Определения Определение 5. Пусть дано семейство случайных величин Определение, данное выше, эквивалентно любому другому из нижеперечисленных. Две случайные величины X, Y независимы тогда и только тогда, когда: Для любых A, B · · Для любых борелевских функций · Для любых ограниченных борелевских функций f,g: R→R:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
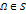
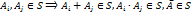
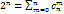 (всевозможные сочетания из n по m элементов)
(всевозможные сочетания из n по m элементов)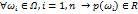 удовлятворяющую следующим условиям:
удовлятворяющую следующим условиям: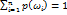
 -сумма вероятностей элементарных событий составляющих событие А.
-сумма вероятностей элементарных событий составляющих событие А. — фиксированное вероятностное пространство. Пусть
— фиксированное вероятностное пространство. Пусть  два
два . Тогда условной вероятностью события A при условии события B называется
. Тогда условной вероятностью события A при условии события B называется |B)=
|B)= 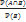
 Круговая диаграмма Венна для условной вероятности
Круговая диаграмма Венна для условной вероятности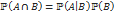
 , то изложенное определение условной вероятности неприменимо.
, то изложенное определение условной вероятности неприменимо.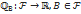 заданная формулой
заданная формулой ,
, и
и 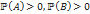 , то
, то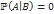 и
и  .
. , а вероятность того, что человек доживет до 90 лет
, а вероятность того, что человек доживет до 90 лет 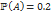
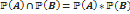 (если независимы) но так как вероятности зависимы, то пересечение вероятности будет 0,2
(если независимы) но так как вероятности зависимы, то пересечение вероятности будет 0,2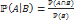 0,2/0,3 = 2/3 ≈ 0,67
0,2/0,3 = 2/3 ≈ 0,67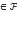 независимы, если
независимы, если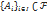 , где I — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть
, где I — произвольное индексное множество. Тогда эти события попарно независимы, если любые два события из этого семейства независимы, то есть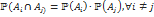
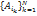 верно:
верно: .
. две сигма-алгебры на одном и том же вероятностном пространстве. Они называются независимыми, если любые их представители независимы между собой, то есть:
две сигма-алгебры на одном и том же вероятностном пространстве. Они называются независимыми, если любые их представители независимы между собой, то есть: .
.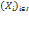 , так что
, так что  . Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры
. Тогда эти случайные величины попарно независимы, если попарно независимы порождённые ими сигма-алгебры  . Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.
. Случайные величины независимы в совокупности, если таковы порождённые ими сигма-алгебры.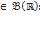 :
: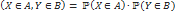
 случайные величины f(X), g(Y) независимы.
случайные величины f(X), g(Y) независимы.