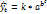|
|
В социально экономических исследованиях.На практике для описания тенденции развития широко используют модели кривых роста представляющих собой различные функции времени Процедура прогноза: § 1 этап: Выбор одной или нескольких кривых форма которых соответствует характеру изменения временного ряда. § 2 этап: Оценка параметров выбранных кривых. § 3 этап: Оценка адекватности выбранных прямых прогнозируемому процессу, оценка точности модели, окончательный выбор кривых роста. § 4 этап: Расчет прогноза. Существуют различные разновидности кривых роста . эти модели могут быть разделены на 3 класса (3 типа) в зависимости от того какой тип динамики они описывают: 1. Функции используемые для описания процессов с монотонным характером тенденции развития и отсутствием пределов роста. Эти условия подходят для многих экономических показателей, таких как промышленное производство в натуральном выражении. 2. Кривые имеющие в исследуемом периоде предел роста, с такими процессами чаще всего сталкиваются в демографии при изучении потребности в товарах и услугах, это кривые насыщения. 3. Если кривые насыщения имеют точки перегиба, то они относятся с C - образным кривым и 3 типу кривых роста. Они описывают 2 последовательных, лавинообразных процесса (прирост зависит от уже достигнутого уровня, один участок с ускорение другой с замедлением). S – образные кривые находят применение в демографическом исследовании, прогнозирование научно технического процесса, прогнозирование спроса на новый вид продукции. Среди кривых роста 1 типа (1 класса) можно выделить класс полиномов.
t –независимая переменная (в данном случае время). Обычно в экономических исследованиях ПОЛИНОМЫ не выше 3-го порядка. Использовать более высокие степени не целесообразно, поскольку полученные таким образом функции будут отражать случайные отклонения. Оценки параметром модели находятся методом наименьших квадрантов
Системы для оценивания ПОЛИНОМОВ не высоких степеней выглядит следующим образом:
Другой подход к упрощению расчетов заключается в переносе начала ординат в середину ряда динамики, это позволит упростить сами уравнения и уменьшить абсолютные значения вершин участвующих в расчете. Если до переноса начала координат для временного параметра использовались значения n= 1,2,3,4,…n, то после переноса: 1. Для четного числа n= -5, -3, -1, 1, 3, 5, …….. (2p-1). 2. Для нечетного числа n =-1, -2, -3,…… (2p+1). Формула для определения коэффициентов линейной и параболической модели после переноса начала координат в середину ряда динамики. § Линейная § Параболическая
На практике используется класс экспоненциальных кривых, которые хорошо описывают процесс, имеющий лавинообразный характер.
После переноса начала координат в середину ряда динамики получается следующее значение
Когда процесс характеризуется насыщением его описывают с помощью кривой, которая имеет отличную от нуля асимптому Если параметр а отрицателен, то асимптома находится выше кривой. Если а положителен, то ниже. При решении экономических задач можно определить значение асимптомы исходя из свойств прогнозируемого процесса. Например, коэффициент использования оборудования не будет ниже единицы. Иногда асимптома задается экспертным путем. Если воздействия ограничивающего фактора начинает сказываться только после определенного момента в точке перегиба, до которого процесс развивался по экспоненте, то для выравнивания используют s-образные модели наиболее известная из них – кривая Гомперца

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , при таком подходе изменения исследуемого показателя связывают лишь с течением времени. Считается, что влияние других факторов не существенно или косвенно связывается через фактор времени. Прогнозирование на основе модели кривых роста базируется на экстраполяции, при этом предполагается, что во временном ряду используют тренд. Характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений.
, при таком подходе изменения исследуемого показателя связывают лишь с течением времени. Считается, что влияние других факторов не существенно или косвенно связывается через фактор времени. Прогнозирование на основе модели кривых роста базируется на экстраполяции, при этом предполагается, что во временном ряду используют тренд. Характер развития показателя обладает свойством инерционности, сложившаяся тенденция не должна претерпевать существенных изменений.
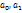 – параметры зависимости.
– параметры зависимости.



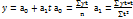

 *
* 

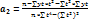
 , где а характеризует начальные условия развития, b–постоянный темп роста.
, где а характеризует начальные условия развития, b–постоянный темп роста. ;
; 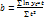
 , где k - горизонтальная асимптота.
, где k - горизонтальная асимптота.