
|
|
Получение трехфазной симметричной системы ЭДС в промышленности
Под фазой в трехфазных цепях понимают обмотку генератора вместе с присоединенной к ней внешней цепью. Нагрузка в трехфазных цепях бывает симметричной, если Za = Zb = Zc, и несимметричной. Способы соединения источника и приемников в трехфазных цепях: 1. Соединение звездой с нулевым (нейтральным) проводом (четыре провода). Применяется при любой нагрузке. 2. Соединение звездой без нулевого провода (три провода). Применяется при симметричной нагрузке. 3. Соединение треугольником (три провода). Применяется при любой нагрузке.
Трехфазная цепь, соединенная звездой
В показанной на рис. 1.26 трехфазной цепи
Рис. 1.26. Трехфазная цепь при соединении источника и приемников звездой
В трехфазных цепях различают фазные и линейные напряжения и токи. Фазное напряжение – это напряжение между началом и концом фазы ( Линейное напряжение – это напряжение между фазами. В цепи, соединенной по типу «звезда», фазный ток равен линейному ( Связь между фазными Uф и линейными Uл напряжениями. Анализируя схему по второму закону Кирхгофа, имеем
Из векторной диаграммы (рис. 1.27) имеем Для источника это равенство справедливо всегда.
Рис. 1.27. Векторная диаграмма напряжений (а) и соотношение между Uли Uф(б) Связь между фазным напряжением источника и фазным напряжением приемника. Из второго закона Кирхгофа для схемы на рис. 1.26 имеем
Вектор смещения нейтрали делает систему напряжений на фазах приемника несимметричной (рис. 1.28). Вектор смещения нейтрали определяем методом узлового напряжения:
где
а) при симметричной нагрузке
так как б) при наличии нулевого провода
При симметричной нагрузке или при наличии нулевого провода (с Только в этих случаях на нагрузке Токи в нагрузках определяются по закону Ома, а ток
При симметричной нагрузке токи образуют симметричную систему и Алгоритм расчета трехфазной цепи, соединённой звездой: Определяем линейные или фазные напряжения источника (1). По формуле (5) определяем напряжение По формулам (4) определяем напряжения на фазах приемника. По формулам (6) определяем токи в фазах приемника и в нулевом проводе. Строим векторную диаграмму.
Трехфазная цепь, соединенная треугольником (рис. 1.29)
Рис. 1.29. Трехфазная цепь при соединении источника и приемников треугольником
В цепи, соединенной треугольником, линейные напряжения равны фазным. На нагрузку всегда действует симметричная система напряжений. Связь между
2. Определение фазных токов в нагрузке:
Алгоритм расчета цепи, соединенной треугольником: 1. По формуле (8) определяем фазные токи. 2. По формуле (7) через фазные токи определяем линейные токи. 3. Строим векторную диаграмму.
а Рис. 1.30. Примеры симметричной (а) и несимметричной (б) нагрузок
Рис. 1.31. Векторные диаграммы для симметричной (а) и несимметричной (б) нагрузок Векторная диаграмма для симметричной нагрузки представлена на рис 1.31, а, для несимметричной – на рис. 1.31, б. Из рис 1.31, а следует, что токи образуют симметричную систему и при симметричной нагрузке

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
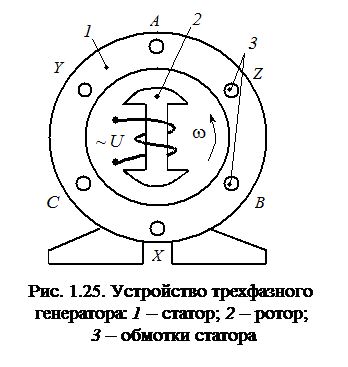 Трёхфазную симметричную ЭДС получают с помощью трёхфазных синхронных генераторов (рис. 1.25). Для этого одинаковые обмотки в статоре располагают под углом 120°. При вращении ротора создаваемое им магнитное поле индуцирует в одинаковых обмотках одинаковые синусоидальные ЭДС. Сдвиг обмоток в пространстве обусловливает сдвиг синусоидальных ЭДС по фазе на угол 120°.
Трёхфазную симметричную ЭДС получают с помощью трёхфазных синхронных генераторов (рис. 1.25). Для этого одинаковые обмотки в статоре располагают под углом 120°. При вращении ротора создаваемое им магнитное поле индуцирует в одинаковых обмотках одинаковые синусоидальные ЭДС. Сдвиг обмоток в пространстве обусловливает сдвиг синусоидальных ЭДС по фазе на угол 120°.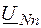 – вектор смещения нейтрали; N – нейтраль источника; n – нейтраль приемника.
– вектор смещения нейтрали; N – нейтраль источника; n – нейтраль приемника.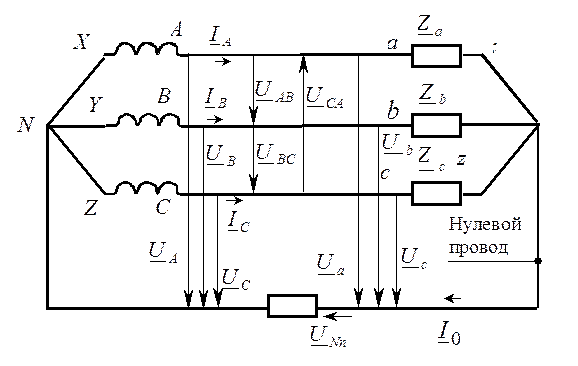
 – фазные напряжения источника;
– фазные напряжения источника; 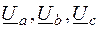 – фазные напряжения приемника).
– фазные напряжения приемника).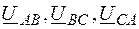 – линейные напряжения;
– линейные напряжения;  – линейные (фазные) токи).
– линейные (фазные) токи).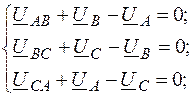
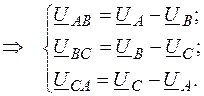 (3)
(3)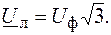
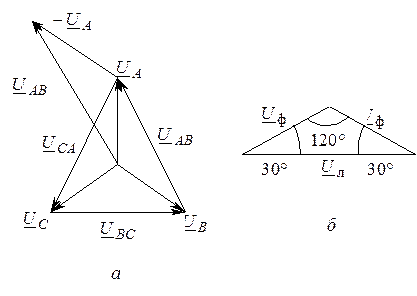
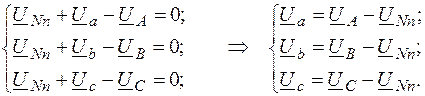 (4)
(4)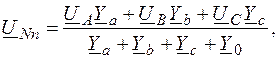 (5)
(5) – проводимости соответствующих фаз приёмника и цепи нулевого провода.
– проводимости соответствующих фаз приёмника и цепи нулевого провода.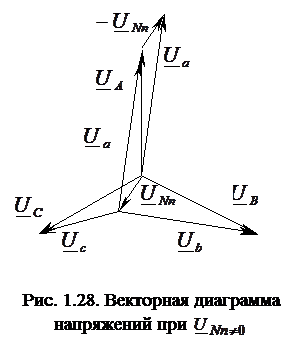 Случаи, когда вектор смещения нейтрали равен нулю:
Случаи, когда вектор смещения нейтрали равен нулю: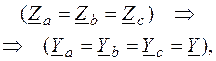
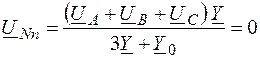 ,
,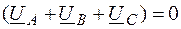 ;
;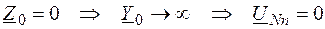 .
.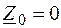 )
) 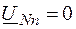 , следовательно, система напряжений приемника совпадает с системой напряжений источника, и значит, она симметрична.
, следовательно, система напряжений приемника совпадает с системой напряжений источника, и значит, она симметрична.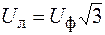 .
.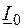 – по закону Кирхгофа:
– по закону Кирхгофа:  (6)
(6) , следовательно, нулевой провод не нужен.
, следовательно, нулевой провод не нужен.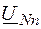 .
.
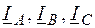 – линейные токи (Iл);
– линейные токи (Iл); 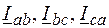 – фазные токи
– фазные токи 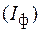 .
.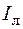 и
и 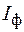 :
: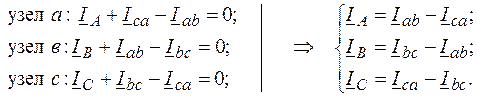 (7)
(7) (8)
(8)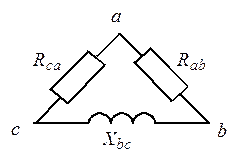
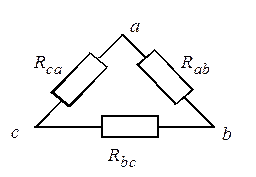 Приведем два примера нагрузок (рис. 1.30) и соответствующих им векторных диаграмм (рис. 1.31).
Приведем два примера нагрузок (рис. 1.30) и соответствующих им векторных диаграмм (рис. 1.31). б
б
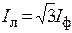 . При несимметричной нагрузке токи не образуют симметричной системы и
. При несимметричной нагрузке токи не образуют симметричной системы и  .
.