
|
|
Цепь с последовательным соединением R, L, C(рис. 1.17)
Рис. 1.17. Цепь с последовательным соединением R, L, C (а) и векторные диаграммы: б – цепь носит активно-индуктивный характер; в – цепь носит активно-емкостный характер
В зависимости от соотношения UL и UC (xL и xC)цепь может носить активно-индуктивный, активно-емкостный или чисто активный характер. Последний случай рассмотрим отдельно. Из векторной диаграммы имеем
Закон Ома для цепи с
здесь Z – полное сопротивление. Треугольники напряжений, сопротивлений И мощностей
Из векторной диаграммы цепи с последовательным соединением
где cos j – коэффициент мощности,
Согласно закону Ома Делим каждую сторону треугольника напряжений на ток и получаем треугольник сопротивлений:
Умножаем каждую сторону треугольника напряжений на ток, и получаем треугольник мощностей:
здесь P – активная мощность [Вт]; S – полная мощность, вырабатываемая источником [ВА]; Q – реактивная мощность [ВАр]. Коэффициент мощности Резонанс в последовательной цепи (резонанс напряжений)
Под резонансом в электрической цепи понимают такое ее состояние, когда ток и напряжение совпадают по фазе и вся цепь ведет себя как чисто активная (рис. 1.18).
Рис. 1.18. Резонансная цепь (а) и векторная диаграмма при резонансе (б)
1.
2. 3.
Если 4.
т.е. цепь из сети реактивную мощность не потребляет и в сеть её не отдает;
В момент резонанса происходит обмен энергии между L и C. Из сети реактивная мощность не потребляется и в сеть не отдается, следовательно, цепь ведет себя как чисто активная.
Цепь с параллельным соединением. Графоаналитический метод расчета
Алгоритм расчета цепи рассмотрим на примере рис. 1.19.
Рис. 1.19. Рассчитываемая цепь (а) и её векторная диаграмма (б)
Алгоритм расчёта: 1.Определяем полные сопротивления ветвей
2.По закону Ома определяем токи в ветвях:
3.Строим векторную диаграмму и определяем общий ток
4.Определяем мощности цепи:
Общие сведения о проводимостях в цепях Переменного тока
Приведем соответствие между сопротивлениями и проводимостями:
Здесь g – активная проводимость; bL – реактивная проводимость цепи с L; bC – реактивная проводимость цепи с С; Y – полная проводимость. Связь между сопротивлением и проводимостью представим формулами
Эквивалентная активная проводимость всей цепи gэ определяется как Эквивалентная реактивная проводимость всей цепи bэ определяется как При этом реактивная проводимость цепи с индексом L (bL) берётся со знаком плюс, а с индексом С (bC) – со знаком минус. Полная проводимость всей цепи определяется по формуле
Резонанс в параллельной цепи (резонанс токов)
Резонансная цепь и векторная диаграмма приведены на рис. 1.20.
Рис. 1.20. Резонансная цепь (а) и векторная диаграмма (б)
При резонансе
Так как

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
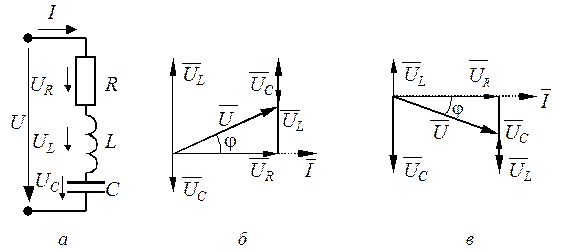
 ;
; 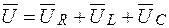 .
.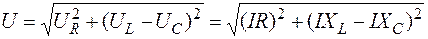 ;
;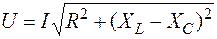 .
. :
: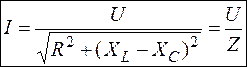 ,
,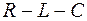 имеем треугольник напряжений:
имеем треугольник напряжений:
 ,
,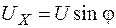 ,
, .
.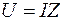 ;
;  ;
; 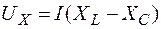 .
.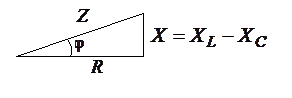
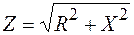 ;
; 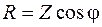 ;
;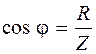 ;
; 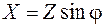 .
.
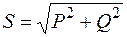 ;
; 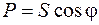 ;
;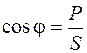 ;
;  ,
,
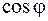 показывает, насколько эффективно и рационально используется энергия. Р характеризует ту часть энергетического процесса, в которой электрическая энергия потребляется приемником и преобразуется в другие виды энергии, т.е. в полезные дела. Q характеризует ту часть энергетического процесса, которая связана с изменением энергии электрического поля емкости или магнитного поля индуктивности. Реактивная мощность не совершает полезной работы, т.к. электрическая энергия не преобразуется в другие виды энергии.
показывает, насколько эффективно и рационально используется энергия. Р характеризует ту часть энергетического процесса, в которой электрическая энергия потребляется приемником и преобразуется в другие виды энергии, т.е. в полезные дела. Q характеризует ту часть энергетического процесса, которая связана с изменением энергии электрического поля емкости или магнитного поля индуктивности. Реактивная мощность не совершает полезной работы, т.к. электрическая энергия не преобразуется в другие виды энергии.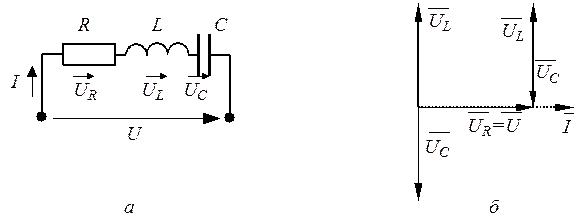
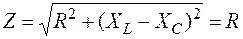 (из определения резонанса);
(из определения резонанса);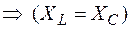 (условие резонанса напряжений);
(условие резонанса напряжений);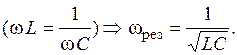
 ;
; ;
;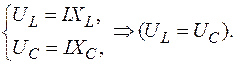
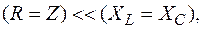 то
то  , т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи.
, т.е. напряжение на реактивных элементах цепи может быть больше напряжения, подводимого ко всей цепи. ,
,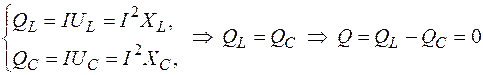 ,
, ;
; .
.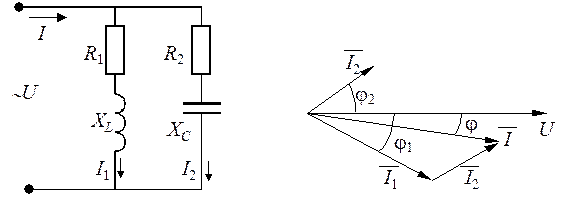 а б
а б :
: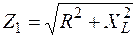 ;
;  .
.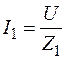 ,
, 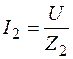 .
. . Углы
. Углы  и
и  для построения векторов тока определяем из треугольника сопротивлений:
для построения векторов тока определяем из треугольника сопротивлений: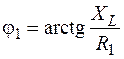 ;
; 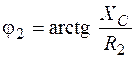 .
.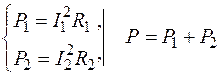 ;
; 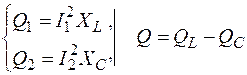 ;
;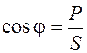 (можно определить и из векторной диаграммы).
(можно определить и из векторной диаграммы). ,
,
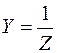 ,
,
 ,
,
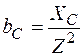 .
.
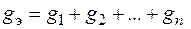 , где g1, g2, …, gn – активные проводимости ветвей.
, где g1, g2, …, gn – активные проводимости ветвей.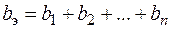 , где b1, b2, …, bn – реактивные проводимости.
, где b1, b2, …, bn – реактивные проводимости.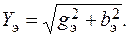

 ;
;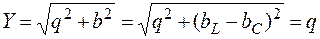 (из определения резонанса)
(из определения резонанса) 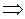
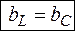 – условие резонанса.
– условие резонанса.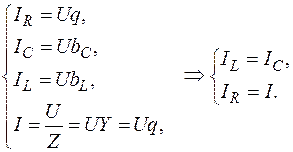
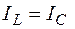 и общий ток равен току, протекающему через активное сопротивление. Если
и общий ток равен току, протекающему через активное сопротивление. Если  , то
, то  , т.е. общий ток меньше тока в реактивных элементах.
, т.е. общий ток меньше тока в реактивных элементах.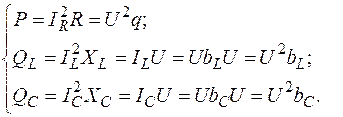
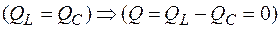 , то
, то 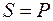 и
и 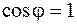 .
.