
|
|
Методы расчета электрических цепейВозможны две постановки задачи расчета электрической цепи: Прямая задача: известны E и R, найти I. Обратная задача: известны часть E, часть R и часть I, найти недостающие параметры. Обе задачи решаются одинаковыми методами. Рассмотрим некоторые из них. Метод эквивалентного сопротивления
Предназначен для расчета цепей с одним источником питания. Алгоритм: 1. Определяем эквивалентное сопротивление цепи. 2. Определяем общий ток в неразветвленной части схемы по закону Ома. 3. Определяем напряжение на разветвленных участках схемы. 4. По закону Ома определяем токи в ветвях. Пример расчета (рис. 1.6):
Рис. 1.6. Пояснение к методу эквивалентного сопротивления
Метод непосредственного использования Законов Кирхгофа
Может применяться для любых цепей. Алгоритм: 1. Определяем число узлов и ветвей в цепи и произвольным образом направляем токи в ветвях. 2. Составляем максимально возможное число уравнений по первому закону Кирхгофа (на единицу меньше числа узлов). 3. Недостающие уравнения составляем по второму закону Кирхгофа (общее число уравнений должно быть равно числу неизвестных токов, т.е. числу ветвей). 4. Решая полученную систему линейных уравнений, определяем неизвестные токи. Недостатком метода является необходимость решения систем уравнений. Приведем пример расчета цепи по законам Кирхгофа. Дано: Определить I1, I2, I3.
Рис. 1.7. К пояснению метода непосредственного использования законов Кирхгофа Решение: для узла а для I для II
Метод узлового напряжения
Применяется для расчета цепей, в которых имеется два узла (рис. 1.8, а).

а б Рис. 1.8. К пояснению метода узлового напряжения
Для фрагмента цепи (рис. 1.8, б) имеем
Для узла а (рис. 1.8, а) имеем
здесь n – число ветвей. Алгоритм: 1. Направляем все ЭДС к одному узлу. Если направление какой-либо ЭДС не совпадает с выбранным нами направлением, то изменяем его и одновременно изменяем знак у этой ЭДС. 2. Направление токов выбираем совпадающим с направлением ЭДС. 3. Используя формулы (1), (2), находим узловое напряжение и токи в ветвях.
Метод суперпозиции
Применяется только для линейных цепей. Основан на использовании принципа суперпозиции. Принцип суперпозиции: ток, протекающий под воздействием нескольких ЭДС, равен алгебраической сумме частичных токов, протекающих от каждой из ЭДС в отдельности. Алгоритм: 1. Оставляем в цепи одну ЭДС, все остальные полагаем равными нулю, и рассчитываем частичные токи, протекающие под воздействием этой ЭДС. 2. Оставляем в цепи другую ЭДС, остальные полагаем равными нулю, и рассчитываем частичные токи. 3. И так далее столько раз, сколько ЭДС. 4. Действительный ток, протекающий под воздействием всех ЭДС, определяем как алгебраическую сумму частичных токов. Этот метод рационально использовать, когда число ЭДС много меньше числа ветвей. Рассмотрим пример расчета:
а б
в г
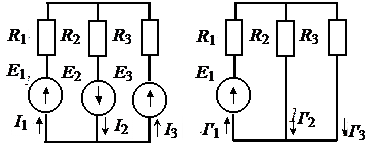
Рис. 1.9. Исходная схема (а) и схемы для определения частичных токов (б – г) – рассчитываем цепь и находим – рассчитываем цепь и находим – рассчитываем цепь и находим – на заключительном этапе определяем
Знаки у частичных токов берем с учетом их направления. Цепи переменного тока
Пусть для передачи энергии мощностью P = 1000 Bт 1) 2) Первый вариант предпочтительнее для передачи энергии, так как в этом случае существенно меньше потери на нагрев проводов ЛЭП Таким образом, передавать энергию выгодно при высоком напряжении, а потреблять, из соображений техники безопасности, при низком. Основная причина, по которой применяют переменный ток, – необходимость преобразования электрической энергии в энергию высокого напряжения перед ее передачей и обратно после ее передачи. Эти преобразования сравнительно просто делаются только в цепях переменного тока. Переменный ток – это такой изменяющийся по величине и направлению ток, среднее значение которого за период равно нулю. Наиболее предпочтительный закон изменения тока – синусоидальный. Преимущества переменного синусоидального тока: · более высокие энергетические показатели работающих на нем машин; · более простой расчет электрических цепей; · производная от синусоидальной функции есть синусоидальная функция. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|

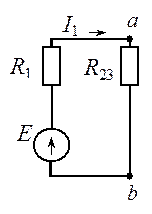
 ;
; 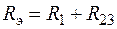 ;
;  ;
; ;
;  ;
;  .
.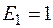 В,
В, 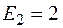 B,
B,  В,
В,  Ом,
Ом,  Ом,
Ом,  Ом.
Ом.
 ;
; ;
; 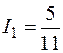 А;
А;  А;
А;  А;
А; .
. , где k – номер ветви;
, где k – номер ветви;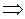
 ;
; 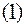
 .
.
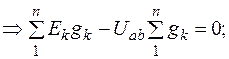
 ;
; ,
, 

 (рис. 1.9, б);
(рис. 1.9, б); (рис. 1.9, в);
(рис. 1.9, в); (рис. 1.9, г);
(рис. 1.9, г);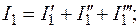
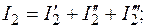
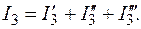
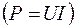 есть два варианта:
есть два варианта: В,
В,  А;
А; В,
В,  А.
А. .
.