
|
|
Стадия разветвления цепей.Разветвлением цепей называется стадия цепного процесса, в кото-рой из одного активного центра образуется несколько.Так, любая цепная реакция складывается из этих четырех элементарных ста-дий, при чем стадия разветвления цепей может не иметь место. Цеп-ные реакции идущие с разветвл-ением цепей называются цепны-ми разветвленными реакциями ЦРР.(рис31)Если ветвление цепей не происходит в цепном процессе, то такая реакция называется цеп-ной неразветвленной реакцией ЦНР.(рис32) Длина цепи.Совокупность пос-ледовательных реакций стадии продолжения цепи, из многокра-тного повторения которых скла-дывается цепной процесс, назы-вается звеном цепи. Звено цепи чаще всего состоит из двух элеме-нтарных реакций (возможно так-же большее их количество, напри-мер, четыре).Число полных зве-ньев приходящихся в среднем на каждый свободный радикал, обра-зовавшийся в стадии зарождения цепи, называется длиной цепи. Цепь может иметь конечную дли-ну из-за наличия стадии обрыва цепи, поэтому длина цепи опреде-ляется соотношением скоростей процессов обрыва и продолжения цепи.Пусть β – вероятность того, что на данном конкретном звене произойдет обрыв цепи, тогда 1-β – вероятность того, что цепь бу-дет продолжаться. Вероятность того, что цепь будет иметь длину n (т.е. цепь n раз продолжиться), а на n+1 произойдет обрыв, будет
на них будет реализовано m коли-чество звеньев
Всего в этом сосуде реализовано звеньев будет
Длина цепи
,т. к. ряд сходящийся, поменяем порядок суммирования и диффе-ренцирования
1-β<1, так как β является вероятностью, а вероятность все-гда меньше единицы. Тогда сумма представляет собой геометриче-скую прогрессию со знаменате-лем (1-β), сумма бесконечно убывающей геометрической про-грессии определяется по формуле
Таким образом, длина цепи
Скорость цепной неразветвле-нной реакции ЦНР.Поскольку при каждом акте зарождения цепи далее следует развитие n звеньев цепи, то скорость цепной реакции будет пропорциональна как длине цепи, так и скорости зарождения цепи Исходя из этого простого соот-ношения, возникает возможность управлять и изменять скорость ЦНР. 1). Скорость ЦНР может быть существенно увеличена воздейст-вием малых добавок в реакцио-нную систему веществ, которые способствуют образованию сво-бодных радикалов, т. е. сущест-венно увеличивают ω0, такие вещества называются инициато-рами. 2). Скорость ЦНР может быть значительно увеличена воздейст-вием на систему физических аген-тов, например, света или ионизи-рующих излучений, которые спо-собствуют образованию активных центров (фактически тем самым увеличиваем ω0, а, следовательно, ωЦНР). 3). Скорость ЦР в газовой фазе при небольших давлениях, как правило, сильно зависит от раз-меров реакционного сосуда, мате-риала, стенок реактора и их сос-тояния. Это связано с тем, что в газовых реакциях при небольших давлениях свободные радикалы, ведущие процесс, сравнительно легко диффундируют к стенке реакционного сосуда и в резуль-тате захвата стенкой гибнут на ней. Увеличение объема реагиру-ющей системы приводит к тому, что время диффузии к стенке уве-личивается, следовательно, ωг уменьшается, ν увеличивается, ωЦНР возрастает. Специальная об-работка стенок реактора также может увеличить или уменьшить скорость гибели радикалов, сле-довательно, уменьшается или уве-личивается ν, а вместе с ней и ωЦНР. 4. Скорость ЦНР может быть рез-ко уменьшена добавлением в реа-кционную систему специальных добавок – ингибиторов. Ингиби-торы – это вещества, которые де-лают радикалы неспособными ве-сти химический процесс. В этом случае резко увеличивается ско-рость гибели активных центров, следовательно, уменьшается дли-на цепи и скорость самой реак-ции. §15. Полимеризация, как пример ЦНР.Процесс полиме-ризации представляет собой ЦНР. В 1934 году создатель теории цеп-ных реакций Семенов Н. Н. ука-зывал, что рост полимерной цепи обеспечивается наличием на ко-нце растущей макромолекулы свободной валентности, а длина цепи (в смысле цепной теории) равна длине цепи полимера, т. е. числу простых ядер в молекуле полимера.Полимерный процесс в простейшем случае включает три стадии.1. Инициирование.На этой стадии молекула мономера превращается в реакционный центр, т. е. в частицу, имеющую свободную валентность М – исходная молекула мономера, R1 – первый реакционный центр. Это инициирование может проис-ходить различным путем: 1). Термический процесс. Актив-ные частицы образуются из моле-кул мономера под воздействием разогрева, при котором увеличи-вается тепловое движение моле-кул. Энергия теплового движения способствует разрыву связей в молекуле мономера и образуется активный центр. М: 2). Инициирование может проис-ходить под действием света или ионизирующего излучения. Связь рвется и возникает радикал, соде-ржащий одно ядро и две сво-бодные валентности. 3). Часто для инициирования при-меняются специальные вещества инициаторы. Они легко вступают во взаимодействие с молекулой мономера, в результате чего обра-зуется радикал, имеющий свобод-ную валентность где I – инициатор. 2. Развитие цепи.После иници-ирования начинает расти полиме-рная цепь. Ее рост – это последо-вательность реакций типа
3. Обрыв цепи.В процессе поли-меризации есть стадия, которая приводит к обрыву реакционной цепи: 1). Если активные концы двух Ра-стущих молекул встречаются, то они взаимодействуют и образуют конечный продукт – полимер, ко-торый в химическом взаимо-действии больше не участвует.
2). Также может происходить пре-кращение роста цепи в результате взаимодействия растущей молеку-лы с какими-либо постоянными примесями, находящимися в сис-теме или со стенкой сосуда. Осно-вными факторами, которые будут определять процесс полимериза-ции, будут являться рассмотре-нные стадии и гибель цепи за счет взаимодействия двух радикалов (другая гибель будет незначитель-на). Рассмотрим процесс в случае, когда инициирование будет про-исходить с помощью инициатора и определим кинетические зако-номерности. 1). 2). 3).
Будем рассматривать процесс в сосуде с усредненными характе-ристиками. Т. е. в любой точке сосуда концентрация M, Ri и Pj одна и та же, и температура постоянна. Обычно эти условия выполняются в реакторе идеаль-ного смешения, в котором проис-ходит интенсивное перемешива-ние реагирующей смеси.
Ограничимся рассмотрением расхода мономера, т. к. процесс, в принципе, определяется этой величиной (для полимера урав-нения выписывать не будем). Обычно когда исследуется ско-рость расхода мономера можно следить за расходом всех Ради-калов вместе. где R – концентрация радикалов, безразлично какой длины.Если сложить все уравнения типа (2) то получим:
Получаем уравнения
Эти уравнения будут определять скорость и условие окончания процесса. Радикалы – активные частицы, поэтому они быстро вступают во взаимодействие, и их концентрация быстро выходит на постоянный уровень, т.е. также как и в методе квазистационарных концентраций, спустя некий про-межуток времени после запуска процесса в системе устанавлива-ется
Тогда
t1t2 – рабочий промежуток проце-сса, при t<t1 много мономера, при t>t2 мало.
Данное выражение можно проин-тегрировать
Полученная формула справедлива для рабочего промежутка.
Еникалопов Н. С. – «Метод фрон-тальной полимеризации» (исполь-зованы идеи теории горения).(рис34)Движение фронта полимеризации в результате воз-действия высокой температуры приводит к тому, что полимериза-ция идет вдоль по всему реактору. §16. Окисление водорода при низком давлении, как пример ЦРР.Рассмотрим одну из наибо-лее интересных реакций: окисле-ние водорода. Это высокоэнерге-тическая реакция.
Нуссельт, рассматривая водоро-дное пламя, записывал скорость реакции как т. е. как трехмолекулярную реак-цию. В этом была ошибка, поско-льку если бы действительно реак-ция шла как трехмолекулярная, то скорость химического процесса должна монотонно падать по ходу процесса, по крайней мере за счет выгорания. Однако, эксперимент показывал противоположное. Да-же при постоянной температуре скорость реакции резко возра-стала по ходу процесса. Это свя-зано с тем, что данная реакция сложная и проходит по цепному механизму. Процесс зарождения цепи в данной реакции может быть различным. Например, при термическом воздействии могут проходить следующие реакции: 1). 2) 3) 4) 5) (свободный атом водорода актив-ная частица) Возможны и другие механизмы образования цепей. Все они равновероятны, причем маловероятны, но достаточно даже малого количества активных центров, чтобы дальше пошел цепной процесс. Рассмотрим про-должение цепи, когда образуется атом водорода. Тогда развитие цепи идет по механизму: 1) 2) Частицы, радикалы группы 3) При чем, поскольку
Брутто уравнение стадии развития цепи показывает, как на звене це-пи из одного активного центра об-разуется три. И каждый вступает во взаимодействие аналогичным образом. Т.е. на нем реализуется звено цепи и опять из каждого одного активного центра обра-зуется три:
Поэтому, спустя некоторый про-межуток времени после зарож-дения хотя бы некоторых актив-ных центров данная реакция идет с колоссальной скоростью т.к. ко-нцентрация активных центров Всего имеется 30 возможных реа-кций, с учетом обратных, их бу-дет 60 (подтверждено экспериме-нтально), но ведущих будет всего 6, которые отражают основные за-кономерности прохождения про-цесса. Экспериментальное подт-верждение такого механизма бы-ло получено в школе академика Семенова. В эксперименте непо-средственно определились веще-ства, которые присутствовали в реакционной смеси входе проце-сса. Наибольшее количество акти-вных центров связано с §17. Модельное уравнение для ЦРР.Для модели используются 6 реакций из 60, которые присутс-твуют в процессе. Это упрощение позволяет проследить за проце-ссом. В то же время, поскольку это ведущие реакции, они опреде-ляют основные закономерности процесса. В ведущей схеме используем следующую цепочку реакций. Из стадии зарождения цепей возьмем только одну реакцию. 1) 2) 3) 4) Возможен процесс обрыва на стенке: 5) Процесс обрыва в объеме: 6) Не рассматриваем обрыв цепей с
Видно, что эта скорость зависит от концентрации исходных веще-ств
Тогда вместо (2) и (3) получаем
Из (2’), (3’) можем получить ква-зистационарную концентрацию
Сюда входят только концентра-ции исходных веществ и самого атома водорода. Введем обознач-ние Скорость образования цепей ω0=const если [H2] и [O2] постоянны. С учетом (5) прихо-дим к уравнению
Выражение этих величин из (5) соответствует реакции окисления водорода. Однако само уравнение (6) имеет более широкий смысл. Оно используется для многих цепных разветвленных реакций. Только для них будут свои выражения для ω0, g, и f, отли-чные от (5) но смысл будут иметь тот же. Поэтому, если мы рассмо-трим (6) то получим закономер-ности для всех ЦРР, которые подходят под это уравнение. Расс-мотрим решение уравнения (6):
1) Если
2) Если Через каждые
f = 2k1[O2],g= k4+k5[O2][M]От тем-пературы наиболее сильно зави-сит параметр k1, поскольку в соо-тветствующей реакции происход-ит разрыв связи в молекуле кисло-рода O2, для чего требуется энер-гия. Поэтому, чем больше темпе-ратура, тем больше энергия у мо-лекул, и тем быстрее идёт процесс (k1 увеличивается).В реакциях об-рыва (5) и (6) старые связи в мо-лекулах не нарушаются. При об-рыве в объёме образуется радикал Отсюда и следует влияние дав-ления.(рис37)При невысоких дав-лениях g~k4, k4 падает с ростом давления, потому что при низких давлениях k4 зависит от скорости диффузии активных центров к стенке, поэтому с уменьшением давления эта скорость растёт и соответственно возрастает k4.При высоких давлениях основной вк-лад в g будет давать второе слага-емое пропорциональное P2. f вс-егда пропорциональна P, следова-тельно, на графике получим пря-мую линию, наклон которой опре-деляет коэффициент k1.T1<T*<T2 Если Т маленькая (случай T1), то при любых давлениях g<f и реак-ция проходит стационарно. При Т=Т*, существует P*, при котором происходит касание кривых f и g. Во всех остальных случаях f<g, и процесс проходит стационарно. И только при P* наблюдаются кри-тические условия, когда концент-рация активных центров n будет расти линейно во времени. Если Т>T* (случай Т2), то существует два критических давления P1 и P2. При P<P1 и P>P2, f<g, и процесс проходит стационарно, если же P1<P<P2, то f>g, и процесс про-ходит взрывным образом (набл-юдается цепное воспламенение). P2 известно давно, оно связанно с процессом обрыва цепей в объ-ёме. При больших давлениях g становится очень большим (за счет второго слагаемого ~P2) и процесс гибели активных центров в объёме подавляет цепное вос-пламенение. Нижнее критическое давление P1, было открыто Семё-новым, и оно объясняется про-цессом гибели активных центров на стенках сосуда. При низких да-влениях этот процесс становится преобладающим. В результате g становится больше f, и цепное воспламенение подавляется. Обы-чно зависимость цепного воспла-менения изображается в фазовом пространстве (P,T). Если описан-ные режимы и зависимости f и g перенести на этот график, то по-лучается, так называемый, полу-остров воспламенения.(рис38) При T=Т* имеем мыс полуострова воспламенения, V соответствует тепловому механизму, она будет рисоваться, если учитывать зави-симость k1(T).воспламенения. При Т<T* получаем стационар. P1, P2 зависят от температуры. Объём проявляется через параметры k4 и k5. С ростом объёма системы, при прочих равных условиях, умень-шается параметр k4 , зависящий от скорости диффузии к стенкам. Следовательно, улучшаются усло-вия для цепного воспламенения. Замечание: Мы рассмотрели тео-рию цепного воспламенения для окисления водорода в случае, ког-да активный центр атом водорода [ §18. Энергия активации.По кр-айней мере, для газофазных реак-ций возникает следующий вопрос. Почему химические реакции идут сравнительно медленнее при обы-чных температурах? Согласно КТГ при нормальных условиях каждая молекула испытывает в среднем 1010 столкновений в секу-нду. И если бы при каждом столк-новении нужных молекул, а их бы было достаточно много, шел бы химический процесс, то он бы проходил практически мгновенно, но это не соответствует реально-му положению вещей. Изучением этой области химической кинети-ки занимались многие учёные. В частности Вант-Гофф и Аррениус отметили, что чем выше темпера-тура, тем быстрее идет химическ-ий процесс (сильная зависимос-ть). Потому, наличие большого числа неэффективных столкнове-ний объясняется тем, что для то-го, чтобы прошла химическая реа-кция при столкновении нужных молекул необходимо, чтобы энер-гия столкновения молекул была достаточно высока. С повышен-ием температуры, энергия столк-новения молекул повышается, и, следовательно, увеличивается чи-сло эффективных столкновений.Только те столкновения ведут к химической реакции, в которых энергия (колебаний и кинетическ-ая) сталкивающихся молекул бо-льше некоторой минимальной ве-личины. Эта энергия нужна для разрыва старых связей в молеку-лах. Тогда снова возникает вопро-с: как же тогда объяснить экзотермические реакции? Например, реакцию разложения метилнитрата: 2СH3ONO2=N2 + CO2+3H2O+64.45 ккал/моль Этому эффекту также можно дать объяснение. Дело в том, что наря-ду с процессами поглощения теп-ла идут также процессы выделе-ния тепла. Для разрыва старых связей нужна энергия, но при об-разовании новых молекул идёт объединение частей прежних разорвавшихся молекул, и при эт-ом их энергия преобразуется в те-пловую, т.е. выделяется тепло. Ес-ли же идёт только процесс разры-ва, то он всегда эндотермическ-ий.CH3ONO2 = CH3O + NO2 – 61 ккал/моль Фактически, для экзот-ермического процесса суммарный процесс, состоящий из разрыва старых связей и установления но-вых, даёт приход тепла.Поскольку эти процессы разделены во време-ни, то в начале идёт разрыв стар-ых связей, а уж потом устанавли-ваются новые связи.Для начала процесса нужна энергия, поэтому скорость химического процесса сильно зависит от температуры. Проведём механическую анало-гию:Вообразим движущийся ша-рик. (рис39)Чтобы попасть в точ-ку b, ему нужно преодолеть поте-нциальный барьер, для этого он должен обладать достаточной ки-нетической энергией. Только те шарики попадут в b, кинетическая энергия которых Ek ≥ En,где Eп – потенциальная энергия, которая определяет минимальную энерг-ию, которой должен обладать ша-рик, чтобы пройти в положение b. Ek(b)>Ek(a). То же самое происхо-дит в химическом процессе. На рисунке горизонтальная ось соо-тветствует ходу химического про-цесса. Q – тепловой эффект реак-ции.Q>0.Eср a – средняя внутрен-няя энергия исходных молекул. Eср в – средняя внутренняя энергия конечных молекул. Ep – энергия разрыва, соответст-вующая разрыву старых связей в молекулах (потенциальный бар-ьер химического процесса).В химическое взаимодействие всту-пят только те исходные моле-кулы, суммарная энергия которых (внутренняя и кинетическая, получающаяся за счет теплового движения)(рис40) больше либо равна энергии потенциального барьера Ep. Как только разрушены старые связи, идет установление новых, внутренняя энергия кото-рых Ecp в. А, выделившаяся энер-гия переходит в тепловую (увели-чивается тепло системы). Тепло-вой эффект реакцииQ=Ecp a - Ecp в. Q>0 – экзотермический процесс, Q<0 соответствует эндотермиич-ес-кому процессу. Таким образом, из всех столкновений реакциион-но-способных молекул к химиче-ской реакции приводят только те, которые обладают энергией дос-таточной для того, чтобы развали-ть, либо заметно ослабить старые связи. Эта наименьшая, необходи-мая для реакции энергия, называ-ется энергией активации(обыч-но рассчитывается на моль вещес-тва). §19. Элементы теории соударений.Данная теория была разработана и нашла широкое применение для газофазных реакций. Рассмотрим случай бимоле-кулярной реакции. Согласно тео-рии соударений химическое взаи-модействие происходит каждый раз, если сталкиваются молекулы нужного сорта и при этом они об-ладают энергией достаточной для преодоления потенциального бар-ьера реакции. Кроме того, они до-лжны быть ориентированны друг относительно дуга(рис41)нужным образом. При рассмотрении соу-дарения молекул считается, что они имеют форму сферы.Если ст-алкиваются молекулы А и В, то сферы будут иметь радиус rA и rB, соответственно. Расстояние меж-ду их центрами будет равно rА+rВ. Отсюда можно заключить, что столкновение молекулы А с моле-кулой В произойдет, если центр молекулы В столкнется с кругом, площадь которого будет равна S=π(rА+rВ), а центр этого круга бу-дет лежать в центре молекулы А. Таким образом, можно сделать за-ключение о том, что В обяза-тельно столкнётся с А, если она будет находиться в цилиндричес-кой трубе радиуса R=rА+rВ, а ось этой трубы проходит через центр молекулы А в направлении Сечение данной трубы называется сечением соударения, поскольку по нему можно судить о факторе соударения. Его обозначают
где М – молярная масса газа, u – скорость движения молекул этого газа,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Рассмотрим сосуд. Пусть в нем на стадии зарождения цепей возникло N активных цент-ров, тогда число активных цент-ров, длина цепей которых будет n ра-вна
. Рассмотрим сосуд. Пусть в нем на стадии зарождения цепей возникло N активных цент-ров, тогда число активных цент-ров, длина цепей которых будет n ра-вна 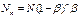 ,
, .
. .
.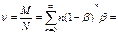
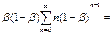
 ,
, .
. , где a1 – первое слагае-мое в сумме, а q – знаменатель прогрессии.Продолжим равенство
, где a1 – первое слагае-мое в сумме, а q – знаменатель прогрессии.Продолжим равенство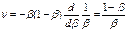 .
. равна отношению веро-ятности продолжения цепи и ве-роятности обрыва (
равна отношению веро-ятности продолжения цепи и ве-роятности обрыва (  длинное звено, b<<1). Можно пе-рейти к скоростям процессов про-должения цепи и обрыва цепи, поскольку вероятности процессов пропорциональны скоростям соо-тветствующих процессов, тогда
длинное звено, b<<1). Можно пе-рейти к скоростям процессов про-должения цепи и обрыва цепи, поскольку вероятности процессов пропорциональны скоростям соо-тветствующих процессов, тогда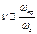 , где
, где 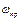 - скорость про-должения цепи. Длина цепи, пре-жде всего, зависит от природы хи-мического процесса, например при окислении водорода (H2+O2):
- скорость про-должения цепи. Длина цепи, пре-жде всего, зависит от природы хи-мического процесса, например при окислении водорода (H2+O2):  звеньев. Кроме того, длина цепи сильно зависит от фи-зических условий, в которых про-ходит цепной процесс.
звеньев. Кроме того, длина цепи сильно зависит от фи-зических условий, в которых про-ходит цепной процесс. ,ν – длина цепи, ω0 – скорость зарождения цепей.
,ν – длина цепи, ω0 – скорость зарождения цепей. ,
, образовав-шаяся часть способна вступать во взаимодействие с другими моле-кулами мономера. Образовался активный центр
образовав-шаяся часть способна вступать во взаимодействие с другими моле-кулами мономера. Образовался активный центр  радикал с 1 ядром мономера и двумя валент-ностями.
радикал с 1 ядром мономера и двумя валент-ностями. ,
,
 , …,
, …,  .
. Такой процесс может идти в сис-теме до тех пор, пока там имеют-ся молекулы мономера.
Такой процесс может идти в сис-теме до тех пор, пока там имеют-ся молекулы мономера. ,где Pi+j – полимер длиной i+j.
,где Pi+j – полимер длиной i+j. ,
,  .
. (kо – константа скорости образования),
(kо – константа скорости образования), ,
, .Кинетические уравнения запишем, используя закон действующих масс:
.Кинетические уравнения запишем, используя закон действующих масс: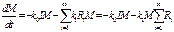 (1)
(1) (2)
(2) ,
,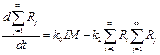
 , (1’)
, (1’) . (2’)
. (2’) ,и поэтому из уравне-ния
,и поэтому из уравне-ния  мы можем найти квазис-тационарную концентрацию R:
мы можем найти квазис-тационарную концентрацию R: .Квазистационарная концентрация Радикала равна
.Квазистационарная концентрация Радикала равна  .
. принимает вид:
принимает вид: - скорость полимеризации (Ра-ботает, когда в системе много по-лимера). Такое приближение дает хороший результат в рабочей ста-дии процесса.(Рис33)
- скорость полимеризации (Ра-ботает, когда в системе много по-лимера). Такое приближение дает хороший результат в рабочей ста-дии процесса.(Рис33) ,(M большая).
,(M большая). ,
, 
 .Согласно нача-льным условиям
.Согласно нача-льным условиям  , тогда
, тогда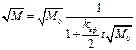 ,
,  .
.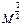 служит формальным приз-наком того, что в реакцию входят свободные радикалы (скорость в степени ½). В конце процесса, ко-гда концентрация M будет мала, определять скорость химического процесса будет первое слагаемое (
служит формальным приз-наком того, что в реакцию входят свободные радикалы (скорость в степени ½). В конце процесса, ко-гда концентрация M будет мала, определять скорость химического процесса будет первое слагаемое (  ).
). 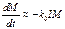 .Тогда
.Тогда  , как это было для случая простой реакции. Если менять температуру системы в хо-де самого процесса, то законноме-рности прохождения процесса бу-дут совершенно другие, посколь-ку меняются k0, k2 и k2. На этом эффекте был разработан новый метод полимеризации:
, как это было для случая простой реакции. Если менять температуру системы в хо-де самого процесса, то законноме-рности прохождения процесса бу-дут совершенно другие, посколь-ку меняются k0, k2 и k2. На этом эффекте был разработан новый метод полимеризации: .
. ,
,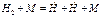 , (0’)
, (0’) , (0’’)
, (0’’) , (0’’’)
, (0’’’)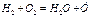 , (0VI)
, (0VI)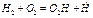 . (0V)
. (0V) , I
, I , II
, II и
и  более активны в химическом отношении, чем
более активны в химическом отношении, чем  и быстрее его вступают во взаимодействие.
и быстрее его вступают во взаимодействие. . III
. III .
.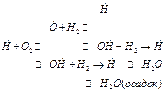
 (kо –кон-станта скорости образования). Ра-дикал
(kо –кон-станта скорости образования). Ра-дикал 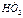 очень неактивен, далее идет основная стадия – стадия ра-звития цепей и ветвления:
очень неактивен, далее идет основная стадия – стадия ра-звития цепей и ветвления: (реакция 1-го порядка по
(реакция 1-го порядка по 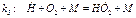
 .Для нас важно оп-ределить закон изменения конце-нтрации атомов водорода. Из за-писанной схемы определим ско-рость изменения концентрации атомов водорода согласно закону действующих масс.
.Для нас важно оп-ределить закон изменения конце-нтрации атомов водорода. Из за-писанной схемы определим ско-рость изменения концентрации атомов водорода согласно закону действующих масс.
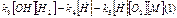
 ,
,  , и от концентрации всех радикалов
, и от концентрации всех радикалов 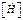 ,
,  ,
,  . Для упрощения можно считать, что концентрации исходных ве-ществ постоянны, а изменение остальных надо записать
. Для упрощения можно считать, что концентрации исходных ве-ществ постоянны, а изменение остальных надо записать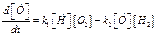 , (2)
, (2)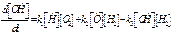 , (3)- нелинейные уравнения, поэ-тому приближенное решение сис-темы с использованием метода квазистационарных концентра-ций. Поскольку
, (3)- нелинейные уравнения, поэ-тому приближенное решение сис-темы с использованием метода квазистационарных концентра-ций. Поскольку 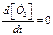 ,
, 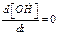 .
.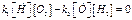 , (2’)
, (2’)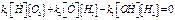 (3’)Таким образом, имеем сист-ему из уравнений (1), (2’) и (3’).
(3’)Таким образом, имеем сист-ему из уравнений (1), (2’) и (3’).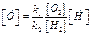 ,а из (3’) с испо-льзованием (2’) найдем квазиста-ционарную концентрацию
,а из (3’) с испо-льзованием (2’) найдем квазиста-ционарную концентрацию  .Тогда для
.Тогда для  (4)
(4) ,
,  ,
,  ,
, 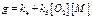 .(5)
.(5) .(6)Уравнение (6) называется уравнением Семе-нова, оно определяет кинетику изменения концентраций активн-ых центров в ЦРР.В соответствии со смыслом в (6):ω0 – это ско-рость образования цепей,g – кон-станта скорости гибели цепей (
.(6)Уравнение (6) называется уравнением Семе-нова, оно определяет кинетику изменения концентраций активн-ых центров в ЦРР.В соответствии со смыслом в (6):ω0 – это ско-рость образования цепей,g – кон-станта скорости гибели цепей (  ),f – константа скорос-ти ветвления цепей
),f – константа скорос-ти ветвления цепей  .
. ,Тогда
,Тогда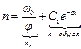 (
( 
 ).Согласно начальным условиям n(0)=0, константа
).Согласно начальным условиям n(0)=0, константа  . Получаем
. Получаем . (7)
. (7)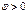 ,
,  (рис35)
(рис35) ,и это стацио-нарное значение будет тем мень-ше, чем больше φ. Минимальное значение будет достигаться в случае отсутствия ветвления цеп-ей:
,и это стацио-нарное значение будет тем мень-ше, чем больше φ. Минимальное значение будет достигаться в случае отсутствия ветвления цеп-ей: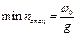 при f=0.
при f=0.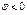 ,
,  :
: 
 (рис36)
(рис36) концентра-ция активных центров будет уве-личиваться в е раз, т. е. концен-трация будет лавинообразно рас-ти, а вместе с ней будет расти и скорость реакции. В этом случае говорят, что происходит цепное воспламенение.Прохождение про-цесса, которое сопровождается резким ускорением реакции в результате прогрессирующего во-зрастания концентрации свобод-ных радикалов при постоянной температуре, называется цепным воспламенением. Заметим, что цепное воспламенение не соответ-ствует тепловому воспламенению. При тепловом воспламенении прогрессирующее возрастание ск-орости реакции происходит в результате прогрессирующего ро-ста температуры.Т.о., имеем два режима прохождения процесса. Случаю f>g соответствует цепное воспламенение (на графике кри-вая II), а случай f<g соответствует выходу реакции на стационарный режим (кривые I). Разделяются эти режимы критическим услов-ием f=g. В этом случае φ=0, и решение уравнения (6) будет
концентра-ция активных центров будет уве-личиваться в е раз, т. е. концен-трация будет лавинообразно рас-ти, а вместе с ней будет расти и скорость реакции. В этом случае говорят, что происходит цепное воспламенение.Прохождение про-цесса, которое сопровождается резким ускорением реакции в результате прогрессирующего во-зрастания концентрации свобод-ных радикалов при постоянной температуре, называется цепным воспламенением. Заметим, что цепное воспламенение не соответ-ствует тепловому воспламенению. При тепловом воспламенении прогрессирующее возрастание ск-орости реакции происходит в результате прогрессирующего ро-ста температуры.Т.о., имеем два режима прохождения процесса. Случаю f>g соответствует цепное воспламенение (на графике кри-вая II), а случай f<g соответствует выходу реакции на стационарный режим (кривые I). Разделяются эти режимы критическим услов-ием f=g. В этом случае φ=0, и решение уравнения (6) будет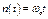 .В этом предельном слу-чае концентрация активных цент-ров растет линейно.Поскольку g и f зависят от различных физичес-ких факторов системы (макроки-нетических факторов), то изменяя макрокинетические параметры можно управлять цепной реакц-ией переходя из взрывного режи-ма f>g в стационарный f<g, и на оборот, обеспечивая нужное про-хождение процесса.На f и g оказывают влияние макропараме-тры системы: P, V и т.д. Расс-мотрим влияние этих параметров в случае окисления водорода.
.В этом предельном слу-чае концентрация активных цент-ров растет линейно.Поскольку g и f зависят от различных физичес-ких факторов системы (макроки-нетических факторов), то изменяя макрокинетические параметры можно управлять цепной реакц-ией переходя из взрывного режи-ма f>g в стационарный f<g, и на оборот, обеспечивая нужное про-хождение процесса.На f и g оказывают влияние макропараме-тры системы: P, V и т.д. Расс-мотрим влияние этих параметров в случае окисления водорода. ]. Их учет вносит поп-равку в теорию, но она не столь существенна ввиду малости их ко-нцентраций. Поэтому, полуостров воспламенения сохраняется в па-раметрах P и T, хотя граница его несколько деформируется.
]. Их учет вносит поп-равку в теорию, но она не столь существенна ввиду малости их ко-нцентраций. Поэтому, полуостров воспламенения сохраняется в па-раметрах P и T, хотя граница его несколько деформируется.  , где
, где 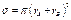 Это сечение можно найти через вязкость газа. Соглас-но МКТГ вязкость:
Это сечение можно найти через вязкость газа. Соглас-но МКТГ вязкость:  ,
,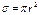 - сечение соударения этого газа,
- сечение соударения этого газа,  - число Авогадро. Отсюда можно найти радиус молекул газа:
- число Авогадро. Отсюда можно найти радиус молекул газа:  . Тогда сечение соударения:
. Тогда сечение соударения:
 В теку-щий момент времени соударение произойдет, если молекула В бу-дет находиться в указанной цили-ндрической трубе, причем на ра-сстоянии u от сечения соударен-ия, проведенного через центр мо-лекулы А.Т.о. можно посчитать объем трубы, молекулы которой столкнутся с молекулой А. С мо-лекулой А столкнутся в текущий момент времени все молекулы со-рта В, которые будут находиться в этой трубе на расстоянии u от ука-занного сечения соударения. Чис-ло соударений:
В теку-щий момент времени соударение произойдет, если молекула В бу-дет находиться в указанной цили-ндрической трубе, причем на ра-сстоянии u от сечения соударен-ия, проведенного через центр мо-лекулы А.Т.о. можно посчитать объем трубы, молекулы которой столкнутся с молекулой А. С мо-лекулой А столкнутся в текущий момент времени все молекулы со-рта В, которые будут находиться в этой трубе на расстоянии u от ука-занного сечения соударения. Чис-ло соударений:  ,где
,где  - концентрация молекул В.Тогда, согласно КТГ можно оценить ско-рость теплового движения:
- концентрация молекул В.Тогда, согласно КТГ можно оценить ско-рость теплового движения: ,k – постоянная Больц-мана (переводит температуру в энергию).
,k – постоянная Больц-мана (переводит температуру в энергию). - приведенная масса молекул. Общее число соударен-ий будет определяться числом со-ударений всех молекул А с молек-улами В в текущую единицу вре-мени. Чтобы получить это число, достаточно знать, сколько в един-ице объема будет молекул A.
- приведенная масса молекул. Общее число соударен-ий будет определяться числом со-ударений всех молекул А с молек-улами В в текущую единицу вре-мени. Чтобы получить это число, достаточно знать, сколько в един-ице объема будет молекул A.