Последовательные реакции.
Дифференциальные уравнения, описывающие кинетику протека-ния последовательных реакций второго и более высокого поря-дка, являются нелинейными. По-этому их решение в большинстве случаев аналитически получить не удается.Рассмотрим две по-следовательные реакции 1-го по-рядка. Схема процесса:
 , ,
Несмотря на простоту, эта схема позволяет определить основные качественные закономерности по-следовательных реакций.
 (зависит от концент-рации промежуточного продукта)(1) (1) (зависит от концент-рации промежуточного продукта)(1) (1)
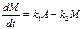 (зависит от конце-нтрации исходного вещества)(2) (2) (зависит от конце-нтрации исходного вещества)(2) (2)
 (3) (3)
Начальные условия:  , ,  . .
Получим первый интеграл сис-темы, сложим (1), (2) и (3):
 , ,
следовательно, получаем
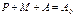 , (4) , (4)
 , (4’)т.о. продукт можно найти, если знать концен-трации A и M. Чтобы из (2) найти M, необходимо найти A, для этого решим уравнение (3): , (4’)т.о. продукт можно найти, если знать концен-трации A и M. Чтобы из (2) найти M, необходимо найти A, для этого решим уравнение (3):  . (5) . (5)
Подставим найденное значение в (2): 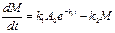
– линейное неоднородное диффе-ренциальное уравнение 1-го по-рядка, его решение складывается из общего решения однородного уравнения и частного решения неоднородного:  .(k1≠k) .(k1≠k)
Используя начальные условия, находим C2, и получаем:  .(6) .(6)
(5) и (6) подставим в (4’), получим изменение концентрации продукта P:
 (7).Таким образом, получены кинетические кривые для всех веществ (A, M, P), для случая (7).Таким образом, получены кинетические кривые для всех веществ (A, M, P), для случая  .Рассмотрим особый случай k1=k2=k. Тогда решение можно по-лучить из (5) и (6). В (6) неопре-деленность раскроем по правилу Лапиталя: .Рассмотрим особый случай k1=k2=k. Тогда решение можно по-лучить из (5) и (6). В (6) неопре-деленность раскроем по правилу Лапиталя:
 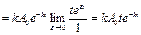
Таким образом, для вещества M получили:  . (6’) . (6’)
Для продукта P: 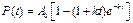 . (7’) . (7’)
Поскольку полученные кинетиче-ские кривые асимптотически стремятся к 0 лишь при t→∞, то время полного химического пре-вращения = ∞.Однако, можно отметить два характерных вре-мени: 1. Время полупревращения по исходному веществу:
 , (когда , (когда  порядка порядка  ). (рис12) ). (рис12)
2.Интересно ведет себя проме-жуточный продукт. Можно найти время, когда он достигает макси-мального значения, продиффере-нцировав (6) или (6’):  , ,
 близко к близко к  , соотве-тственно , соотве-тственно  – среднее время жизни по исходному веществу – среднее время жизни по исходному веществу
 , ,
т. е. согласно (5’) в точке мак-симума A и M совпадают.
Если использовать уравнение (6), когда  , то , то  . .
Значение максимальной концент-рации промежуточного продукта M:  . .
 и и  зависят от со-отношения зависят от со-отношения  и и  : :  > >  или или  < <  . .
Можем использовать (7) или (7’):  . .
Так как M≥0, то кривая P(t) монотонно-возрастающая. Кривизна: 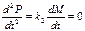
– перегиб достигается в момент  , где , где  – время, когда ко-нцентрация промежуточного про-дукта максимальна. – время, когда ко-нцентрация промежуточного про-дукта максимальна.  , при , при  ; ;  , при , при  . .
Следовательно, в точке перегиба кривизна кривой P(t) переходит с положительной на отрицатель-ную, а сама кривая имеет S-фо-рму. (рис13)  (нем-ного ниже) Рассмотрим два преде-льных слу-чая: 1.k1>>k2 (нем-ного ниже) Рассмотрим два преде-льных слу-чая: 1.k1>>k2  .Это означает, что всё исходное вещество с большой скоростью, по сравне-нию со второй стадией проце-сса, перейдет из исходного веще-ства A в вещество M. После этого будет происходить медле-нное превращение, по сравнению с первой стадией, вещества M в конечный продукт P. .Это означает, что всё исходное вещество с большой скоростью, по сравне-нию со второй стадией проце-сса, перейдет из исходного веще-ства A в вещество M. После этого будет происходить медле-нное превращение, по сравнению с первой стадией, вещества M в конечный продукт P.
Получаем:  , ,
   , следовательно, в преде-льном случае M ведет себя как исходное вещество. (рис14). , следовательно, в преде-льном случае M ведет себя как исходное вещество. (рис14).
M(0)=0,M(0)=A0
Значение M(t) приближенно и не точно в начальный момент вре-мени, когда происходит преоб-разование вещества A в M. Зна-чение M(t) определяется точно по-сле установления процесса, и мак-симум M смещен к начальной ста-дии процесса, т. е. tm мало.При та-ком соотношении констант k1 и k2, для последовательных реак-ций, можно выделить ведущую стадию процесса. Этой стадией является наиболее медленная стадия, она тормозит весь процесс. Закончится химический процесс по завершению второй стадии. 1. k1<<k2 При таком со-отношении констант также можно получить приближенную форму-лу.    Т. е. проме-жуточный продукт M в системе будет находиться в малых коли-чествах, в течение всего процесса, т. к. Т. е. проме-жуточный продукт M в системе будет находиться в малых коли-чествах, в течение всего процесса, т. к.  . Также в системе быстро устанавливается равно-весие между концентрацией исхо-дного вещества и промежу-точного продукта. Говорят, что M(t) будет находиться в квазиста-ционарном состоянии, т. е. его из-менение происходит только бла-годаря изменению A(t). Эти осо-бенности связаны с большой ак-тивностью M.(рис15). Сначала идет установление процесса, . Также в системе быстро устанавливается равно-весие между концентрацией исхо-дного вещества и промежу-точного продукта. Говорят, что M(t) будет находиться в квазиста-ционарном состоянии, т. е. его из-менение происходит только бла-годаря изменению A(t). Эти осо-бенности связаны с большой ак-тивностью M.(рис15). Сначала идет установление процесса,  смещено к началу процесса. На таких особенностях основан ме-тод квазистационарных концент-раций. При таком соотношении констант ведущей стадией проце-сса является более медленная стадия (первая), она тормозит весь процесс, следовательно, оп-ределяет его. Для последователь-ных реакций ведущей стадией процесса является самая медле-нная. смещено к началу процесса. На таких особенностях основан ме-тод квазистационарных концент-раций. При таком соотношении констант ведущей стадией проце-сса является более медленная стадия (первая), она тормозит весь процесс, следовательно, оп-ределяет его. Для последователь-ных реакций ведущей стадией процесса является самая медле-нная.
Параллельные реакции.
Исходное вещество принимает участие в нескольких одновреме-нно протекающих реакциях. Схе-ма таких процессов: 1) n пара-ллельных реакций 1-го порядка:
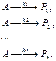
2) схема параллельных реакций 2-го порядка (параллельны по веществу А):
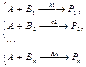
Параллельные реакции еще назы-вают конкурирующими. Сумма-рная скорость расхода вещества A складывается из скоростей прев-ращения по каждому из марш-рутов.При исследовании паралле-льных реакций используется ме-тод сравнительной оценки: пу-сть имеем две параллельные реак-ции:  , n-го порядка. , n-го порядка.
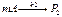 , m-го порядка.Тогда скорость образования продуктов согласно закону действующих масс: , m-го порядка.Тогда скорость образования продуктов согласно закону действующих масс:
 Разделим первое уравнение на второе, получим: Разделим первое уравнение на второе, получим:  .Т. е. образование продуктов будет проходить в строгой пропорции.Если n=m, то получаем наиболее простой слу-чай: .Т. е. образование продуктов будет проходить в строгой пропорции.Если n=m, то получаем наиболее простой слу-чай:  , ,
при условии, что  - начальные концентрации. То есть, концентрации продуктов пропор-циональны соответствующим ко-нстантам скоростей.Если - начальные концентрации. То есть, концентрации продуктов пропор-циональны соответствующим ко-нстантам скоростей.Если  , то , то  .Вывод: ведущей стадией параллельных реакций является наиболее быстрая, по ней будет проходить основное преобразование исходного вещес-тва. Для выяснения характера ки-нетической кривой, рассмотрим схему (1) – параллельные реакции 1-го порядка. Выпишем диффе-ренциальные уравнения, опреде-ляющие изменение концентраций веществ: .Вывод: ведущей стадией параллельных реакций является наиболее быстрая, по ней будет проходить основное преобразование исходного вещес-тва. Для выяснения характера ки-нетической кривой, рассмотрим схему (1) – параллельные реакции 1-го порядка. Выпишем диффе-ренциальные уравнения, опреде-ляющие изменение концентраций веществ:
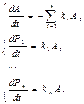
Пусть начальные условия:  , ,  , ,  . .
 .Интегрируем с учетом начальных условий: .Интегрируем с учетом начальных условий: 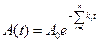
Время полупревращения:  .Скорость прохожден-ия параллельных реакций больше, чем скорость самой быстрой из реакций, входящих в неё. Изме-нение i-го продукта: .Скорость прохожден-ия параллельных реакций больше, чем скорость самой быстрой из реакций, входящих в неё. Изме-нение i-го продукта:   , ,
Согласно начальным условиям  ,т.е. ,т.е.  .Кинетическая кри-вая для P: .Кинетическая кри-вая для P:  .Из последней формулы видно, что продукты образуются в строгой пропорции, определяемой их кон-стантой. В соответствии с этими константами будут находиться продукты после завершения хи-мического процесса. .Из последней формулы видно, что продукты образуются в строгой пропорции, определяемой их кон-стантой. В соответствии с этими константами будут находиться продукты после завершения хи-мического процесса.  , ,  .В конечном состоя-нии: .В конечном состоя-нии: 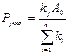 .Две реакции: P1k, P2k – конечные концентра-ции. .Две реакции: P1k, P2k – конечные концентра-ции.   .(рис16) .(рис16)
§9. Последовательно-паралле-льные реакции.Простейшая схе-ма последовательно-параллельной реакции:  По A ре-акция параллельная, по M реакция последовательна По A ре-акция параллельная, по M реакция последовательна  (1) (1)  ,(2 ,(2  (3)Начальные условия: (3)Начальные условия:  , ,  (отсутствуют в на-чальные момент). (отсутствуют в на-чальные момент).
 , , 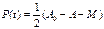 Разделим (1) на (2): Разделим (1) на (2):
  , ,
найдем M(t), подставив A(t) в(2). Полученное выражение M(t) подставим в выражение для A(t), и выразим A(t). Рассмотрим преде-льные случаи:1. k1>>k2 Будет про-являться свойство параллельных реакций, т. е. вещество A по пер-вой стадии преобразуется в про-межуточный продукт M, но т. к. вещества A не останется в систе-ме, то вторая стадия не успеет ре-ализоваться. 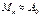  (или очень мало)2. k1<<k2 Будет проя-вляться свойство последователь-ных реакций, поскольку вторая реакция не может быть реалиизо-вана без вещества M. Поэтому ве-дущей стадией будет являться первая реакция – самая медлен-ная. Первая реакция образует про-межуточный продукт M, и он с большой скоростью перерабаты-вается в P. Поэтому активный промежуточный продукт M в сис-теме будет находиться в малых количествах, в пропорции: (или очень мало)2. k1<<k2 Будет проя-вляться свойство последователь-ных реакций, поскольку вторая реакция не может быть реалиизо-вана без вещества M. Поэтому ве-дущей стадией будет являться первая реакция – самая медлен-ная. Первая реакция образует про-межуточный продукт M, и он с большой скоростью перерабаты-вается в P. Поэтому активный промежуточный продукт M в сис-теме будет находиться в малых количествах, в пропорции:  ,т. е. в квазистаци-онарном состоянии. Только в на-чале процесса, пока будет прои-сходить установление квазистаци-онарного состояния M(t) будет от-личаться от данного выражения. ,т. е. в квазистаци-онарном состоянии. Только в на-чале процесса, пока будет прои-сходить установление квазистаци-онарного состояния M(t) будет от-личаться от данного выражения.
 Вывод: для по-следовательно-параллельных ре-акций, в зависимости от соотно-шения констант, могут проявлять-ся свойства как последовательн-ых, так и параллельных реакций. Вывод: для по-следовательно-параллельных ре-акций, в зависимости от соотно-шения констант, могут проявлять-ся свойства как последовательн-ых, так и параллельных реакций.
§10. Автокаталитические реак-ции. Катализ– сложный физико-химический процесс, в котором скорость химической реакции ускоряется присутствием некото-рого вещества – катализатора. Об-ычно катализатор в ходе химичес-кой реакции не расходуется, хотя может портиться. Существует го-могенный и гетерогенный ката-лиз. Будем рассматривать гомо-генный автокатализ.Автокатализ– это явление каталитического вл-ияния продукта реакции на ско-рость реакции (сама реакция по-рождает вещество-катализотор).
Рассмотрим химический процесс:
 , A переходит в продукт P двумя путями: с константой скорости , A переходит в продукт P двумя путями: с константой скорости  как по простой реак-ции 1-го порядка, и с константой скорости как по простой реак-ции 1-го порядка, и с константой скорости  автокаталитической реакцией. Тогда скорость всего химического процесса: автокаталитической реакцией. Тогда скорость всего химического процесса:  Скорость простой реакции Скорость простой реакции  Скорость авто-каталитической реакции Скорость авто-каталитической реакции   , (1) , (1)
 .(2) Начальные условия: .(2) Начальные условия:  , ,  .(3) Выделим первый интеграл, сло-жим (1) и (2): .(3) Выделим первый интеграл, сло-жим (1) и (2):
  (4).Т. о. продукт мож-но определить через концентра-цию исходного вещества, (4) – закон сохранения массы вещес-тва.Перейдем к безразмерным переменным, глубина превраще-ния: (4).Т. о. продукт мож-но определить через концентра-цию исходного вещества, (4) – закон сохранения массы вещес-тва.Перейдем к безразмерным переменным, глубина превраще-ния:
 , следова-тельно , следова-тельно  .Используем уравнение (1) для нахождения η: .Используем уравнение (1) для нахождения η:
 , где , где  – масштабное время, – масштабное время, 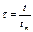 – безразмерное время. – безразмерное время.
 , пусть для удобства , пусть для удобства  .В качестве масштабного времени используем характерное время автокаталитической реакции. .В качестве масштабного времени используем характерное время автокаталитической реакции.  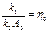
– параметр автокаталитичности, в данном случае, представляет отношение констант простой реакции и эффективной константы автокаталитической реакции.  (5) (5)
Если 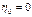 , то химический процесс начаться не может, пос-кольку начальная скорость у него будет равна нулю: , то химический процесс начаться не может, пос-кольку начальная скорость у него будет равна нулю:
 .Т. о. параметр автокаталитичности оп-ределяет исходную (безразмерн-ую в данном случае) скорость реа-кции. Эта величина может быть отлична от 0 по двум причинам. Если .Т. о. параметр автокаталитичности оп-ределяет исходную (безразмерн-ую в данном случае) скорость реа-кции. Эта величина может быть отлична от 0 по двум причинам. Если  , то , то    . .  , ,
Масштабная скорость  . .  Чтобы исходная скорость не равнялась нулю, надо, чтобы Чтобы исходная скорость не равнялась нулю, надо, чтобы  . В на-шем случае эта величина не равна нулю, поскольку в системе парал-лельно с автокаталитической, ид-ет простая реакция с константой скорости . В на-шем случае эта величина не равна нулю, поскольку в системе парал-лельно с автокаталитической, ид-ет простая реакция с константой скорости  , и начинает про-цесс эта простая реакция (играет роль затравки).Если в системе нет параллельной простой реакции, то чтобы начался процесс, необходи-мо присутствие хотя бы малого количества продукта реакции , и начинает про-цесс эта простая реакция (играет роль затравки).Если в системе нет параллельной простой реакции, то чтобы начался процесс, необходи-мо присутствие хотя бы малого количества продукта реакции 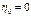 , ,  . Продукт добавля-ют в систему для начала процесса. Можно сделать другое обезразме-ривание с выбором h, тогда (5) примет иной вид. Рассмотрим за-кономерности автокаталитическ-ой реакции согласно задаче (5). Рассмотрим, как меняется скоро-сть автокаталитической реакции в ходе химического процесса. Без-размерная скорость . Продукт добавля-ют в систему для начала процесса. Можно сделать другое обезразме-ривание с выбором h, тогда (5) примет иной вид. Рассмотрим за-кономерности автокаталитическ-ой реакции согласно задаче (5). Рассмотрим, как меняется скоро-сть автокаталитической реакции в ходе химического процесса. Без-размерная скорость
 ,0≤η≤1Рассмотрим зависимость ,0≤η≤1Рассмотрим зависимость  : :
 , берем производную: , берем производную:
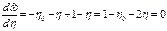 , ,
при  получаем точку экстремума. получаем точку экстремума.  точка максимума. точка максимума.
Значение  в точке максимума: в точке максимума:
  . .
Точка экстремума будет находиться в промежутке  , если , если  .(рис17)Т. о. максимум скорости автокатали-тической реакции будет реали-зовываться в период химического процесса, если только параметр автокаталитичности η0<1. Иначе скорость .(рис17)Т. о. максимум скорости автокатали-тической реакции будет реали-зовываться в период химического процесса, если только параметр автокаталитичности η0<1. Иначе скорость  на промежутке [0,1] будет монотонно падать, также как в случае простой реакции. Обычно для автокаталитических реакций на промежутке [0,1] будет монотонно падать, также как в случае простой реакции. Обычно для автокаталитических реакций  .Обычно определяют не сам скорость хи-мической реакции, а ее отноше-ние к начальной скорости (во ско-лько раз увеличилась, или умень-шилась скорость по отношению к начальной скорости): .Обычно определяют не сам скорость хи-мической реакции, а ее отноше-ние к начальной скорости (во ско-лько раз увеличилась, или умень-шилась скорость по отношению к начальной скорости):
 ;Максимум этого значения ;Максимум этого значения
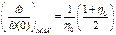
характеризует ускорение химии-ческого процесса. Т. е. чем мень-ше  , тем больше будет ускоре-ние химического процесса.(рис18) , тем больше будет ускоре-ние химического процесса.(рис18)
Определим первую характерную особенность автокаталитической реакции. Она способна самоус-коряться в изотермических усло-виях при  , и это самоускоре-ние будет тем больше, чем мень-ше , и это самоускоре-ние будет тем больше, чем мень-ше  .При маленьких .При маленьких  , говорят о сильном автокатализе ( , говорят о сильном автокатализе (  ).Если ).Если  или или  , то самоускорения нет, и реакция ведет себя как простая. , то самоускорения нет, и реакция ведет себя как простая.
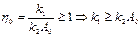 ,т. е. скорость простой реакции больше скорости автокаталитической и она является определяющей. Ра-ссмотрим кинетическую кривую автокаталитической реакции. Для этого проинтегрируем (5). Разделяем переменные: ,т. е. скорость простой реакции больше скорости автокаталитической и она является определяющей. Ра-ссмотрим кинетическую кривую автокаталитической реакции. Для этого проинтегрируем (5). Разделяем переменные:
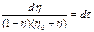 , ,
разложим на простые дроби
 , ,
интегрируем
 , ,
Из начальных условий  , тогда , тогда
 (6) (6)
Можно выразить η(τ)
 (6’) (6’)
При τ→0, η→0,При τ→∞, η→1.Кинетическая кривая η(τ) имеет S-форму, и монотонно воз-растает 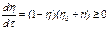
 , когда , когда  .Т. о. кинетическая кривая имеет точку перегиба при .Т. о. кинетическая кривая имеет точку перегиба при  , когда достигается максимум ско-рости автокаталитической реак-ции (рис19). , когда достигается максимум ско-рости автокаталитической реак-ции (рис19). 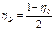
Время достижения максимума скорости автокаталитической реакции и точки перегиба кинетической кривой, определяется из равенства (6) подстановкой  : :
 .Чем меньше .Чем меньше  , тем больше , тем больше  (только в безразмерном виде, т. к. (только в безразмерном виде, т. к.  тоже связано с автокатали-тической реакцией).Если тоже связано с автокатали-тической реакцией).Если  боль-ше, то время достижения боль-ше, то время достижения  будет уменьшаться.Если будет уменьшаться.Если  , то полу-чается кривая , то полу-чается кривая  , точка перегиба совпадает с нулем, S-формы нет, и кинетическая кривая такая же, как для простой реакции 1-го порядка. , точка перегиба совпадает с нулем, S-формы нет, и кинетическая кривая такая же, как для простой реакции 1-го порядка.
При сильном автокатализе  , химический процесс дли-тельное время практически не идет (идет автокаталитическое самоускорение). При достижении некоторой величины η автоката-литическое ускорение становится существенным, и происходит разгон автокаталитической реак-ции, скорость становится больш-ой и химический процесс прохо-дит быстро. Экспериментаторы, тот промежуток времени, когда процесс почти не идет, назвали периодом индукции. Понятие пе-риода индукции является услов-ным, поскольку в зависимости от точности приборов, измеренное время появления продукта будет различно. Поэтому теоретически предложили в качестве периода индукции использовать , химический процесс дли-тельное время практически не идет (идет автокаталитическое самоускорение). При достижении некоторой величины η автоката-литическое ускорение становится существенным, и происходит разгон автокаталитической реак-ции, скорость становится больш-ой и химический процесс прохо-дит быстро. Экспериментаторы, тот промежуток времени, когда процесс почти не идет, назвали периодом индукции. Понятие пе-риода индукции является услов-ным, поскольку в зависимости от точности приборов, измеренное время появления продукта будет различно. Поэтому теоретически предложили в качестве периода индукции использовать  . Эта величина тоже условная для пери-ода индукции, поскольку в момент . Эта величина тоже условная для пери-ода индукции, поскольку в момент  израсходована уже почти половина продукта. израсходована уже почти половина продукта.  . .
Но, поскольку разгон происходит в узком интервале, то
 , ,  – начало разгона (τm и τp почти равны).Рассмотрим случай – начало разгона (τm и τp почти равны).Рассмотрим случай  , он называется случаем простой реакции порядка , он называется случаем простой реакции порядка  , с периодом полупревра щения: , с периодом полупревра щения:  .Если реакция простая, то .Если реакция простая, то  , следовате-льно, по определению , следовате-льно, по определению  .Реакция автокатали-тичная и .Реакция автокатали-тичная и  , следовательно , следовательно
 , ,
 . .
.  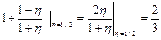
Из формулы (6) при  получаем время полупревраще-ния: получаем время полупревраще-ния:  .Замечание: в общ-ем случае возможен автокатализ n-го порядка по исходному веще-ству A, и m-го порядка по про-дукту P, в этом случае: .Замечание: в общ-ем случае возможен автокатализ n-го порядка по исходному веще-ству A, и m-го порядка по про-дукту P, в этом случае:
 ,и если параллель-но идет простая реакция порядка n, то ее скорость ,и если параллель-но идет простая реакция порядка n, то ее скорость 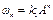 ,Тогда дифференциальное уравнение им-еет вид ,Тогда дифференциальное уравнение им-еет вид
 .Приведем задачу к безразмерному виду, вводя .Приведем задачу к безразмерному виду, вводя  , получим уравне-ние , получим уравне-ние  .Здесь параметр автокаталитичности и .Здесь параметр автокаталитичности и   Примеры: Большинство автокаталити-ческих реакций протекает в жид-кой фазе. Впервые было получено Освальдом в 1883 году, при oму-лении метилацетата CH3COOCH3 Примеры: Большинство автокаталити-ческих реакций протекает в жид-кой фазе. Впервые было получено Освальдом в 1883 году, при oму-лении метилацетата CH3COOCH3
 ,Сначала эксп-ериментально, потом теоретичес-ки.Пример газофазной реакции: термическая диссоциация водоро-да. ,Сначала эксп-ериментально, потом теоретичес-ки.Пример газофазной реакции: термическая диссоциация водоро-да.
 ,M – любая частица, например в аргоне Ar ,M – любая частица, например в аргоне Ar
  – уравнение цепн-ых реакций (Семенов).Многие взрывчатые вещества при низкой температуре реагируют по автока-талитическому механизму (тетрил η0=0,175). В зависимости от тем-пературы, механизм химической реакции может быть различным. – уравнение цепн-ых реакций (Семенов).Многие взрывчатые вещества при низкой температуре реагируют по автока-талитическому механизму (тетрил η0=0,175). В зависимости от тем-пературы, механизм химической реакции может быть различным.
§11. Кинетические уравнения обратимого химического проце-сса.Пусть имеем простую реак-цию:
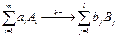 , ,  – стехиометрические коэффициен-ты. Поскольку реакция простая, то, согласно уравнению, можно составить пропорцию по измене-нию концентраций участвующих веществ: – стехиометрические коэффициен-ты. Поскольку реакция простая, то, согласно уравнению, можно составить пропорцию по измене-нию концентраций участвующих веществ:  .Получаем m+l равенств. Продиффере-нцируем: .Получаем m+l равенств. Продиффере-нцируем:  . Согласно закону действующих масс . Согласно закону действующих масс  (произведение по всем i).Де-Донде предложил для исследования процесса Рас-смотреть величину x, которому равна первая пропорция (1). x ха-рактеризует ход процесса, опреде-ляя насколько глубоко прошла ре-акция. В начале процесса x=0, а далее x будет возрастать. В отли-чие от глубины превращения x яв-ляется размерной величиной и соответствует размерности конце-нтрации. Зная x, можно найти все A, и все B. (произведение по всем i).Де-Донде предложил для исследования процесса Рас-смотреть величину x, которому равна первая пропорция (1). x ха-рактеризует ход процесса, опреде-ляя насколько глубоко прошла ре-акция. В начале процесса x=0, а далее x будет возрастать. В отли-чие от глубины превращения x яв-ляется размерной величиной и соответствует размерности конце-нтрации. Зная x, можно найти все A, и все B.
 Уравнение для x найдем из (2), подставив Уравнение для x найдем из (2), подставив  или или   .Реакция может идти как в прямом, так и в обратном направлении. Только при различных темпера-турах состояние химического рав-новесия может быть смещено либо в сторону продуктов, либо в сторону исходных веществ. То ес-ть, если при химическом равнове-сии продуктов почти нет, то гово-рят, что реакция не идет (хими-ческое равновесие смещено в сто-рону исходных веществ). Если при химическом равновесии ис-ходных веществ практически нет, то говорят, что химическая реак-ция идет до конца (химическое равновесие смещено в сторону продуктов).В зависимости от температуры, химическое равно-весие может изменяться, и при определенных температурах, в состоянии равновесия, в смесях могут быть и исходные вещества, и продукты. Рассмотрим законно-мерности химического процесса: .Реакция может идти как в прямом, так и в обратном направлении. Только при различных темпера-турах состояние химического рав-новесия может быть смещено либо в сторону продуктов, либо в сторону исходных веществ. То ес-ть, если при химическом равнове-сии продуктов почти нет, то гово-рят, что реакция не идет (хими-ческое равновесие смещено в сто-рону исходных веществ). Если при химическом равновесии ис-ходных веществ практически нет, то говорят, что химическая реак-ция идет до конца (химическое равновесие смещено в сторону продуктов).В зависимости от температуры, химическое равно-весие может изменяться, и при определенных температурах, в состоянии равновесия, в смесях могут быть и исходные вещества, и продукты. Рассмотрим законно-мерности химического процесса:
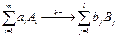 – в пря-мом направлении, – в пря-мом направлении,
 – в обрат-ном направлении.Скорость хи-мического процесса ω, будет оп-ределяться суммой скоростей, с учетом направления: – в обрат-ном направлении.Скорость хи-мического процесса ω, будет оп-ределяться суммой скоростей, с учетом направления:  . Если наступит химическое равно-весие, то суммарная скорость ω=0, тогда: . Если наступит химическое равно-весие, то суммарная скорость ω=0, тогда:
 (4) (4) 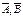 – концентрации, в состоянии хими-ческого равновесия. Равновесные процессы изучаются в равновесной термодинамике. Термодинамичес-кая константа равновесия – концентрации, в состоянии хими-ческого равновесия. Равновесные процессы изучаются в равновесной термодинамике. Термодинамичес-кая константа равновесия
 .Согласно (4), конст-анта .Согласно (4), конст-анта  .Т. о., если реакция простая, то её константа равнове-сия равна отношению констант скоростей прямой и обратной реа-кции. Кинетические закономерно-сти обратимого процесса удобно определять через x. Уравнение д-ля x определяется также из (2), но вместо ω, подставляется ω с уче-том прямой и обратной реакции. Для x получаем уравнение: .Т. о., если реакция простая, то её константа равнове-сия равна отношению констант скоростей прямой и обратной реа-кции. Кинетические закономерно-сти обратимого процесса удобно определять через x. Уравнение д-ля x определяется также из (2), но вместо ω, подставляется ω с уче-том прямой и обратной реакции. Для x получаем уравнение: 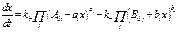
(3’)Уравнение (3’) – обыкновен-ное дифференциальное уравне-ние, с разделяющимися перемен-ными, и его можно разрешить до квадратур. Рассмотрим кинетиче-ские закономерности для простой об-ратимой химической реакции 1-го порядка.
 Тогда урав-нение (3‘) принимает вид: Тогда урав-нение (3‘) принимает вид:
 , ,
 (3’’) (3’’)
– линейное неоднородное диффе-ренциальное уравнение. Началь-ные условия x(0)=0
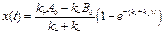 (5Разделим на (5Разделим на  . .
 (5’). (5’).
Из решения (5’) видно, что пере-менная x ведет себя так же, как концентрация продукта в случае простой реакции 1-го порядка, то-лько вместо константы скорости стоит сумма констант скоростей прямой и обратной реакции  . .
При t→∞, система стремится к равновесному состоянию, и  . .
 .Если подставить .Если подставить  в выражения для A и B, то получим их равновесные значения: в выражения для A и B, то получим их равновесные значения:
 ( ( 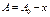 , ,  ) )  , ,  . .
Симметричный вид, и если  , тогда B будет исходным веществом, A продуктом. Т.е. для обратимого процесса трудно ска-зать, что будет исходным вещес-твом, а что продуктом.Изменение во времени: , тогда B будет исходным веществом, A продуктом. Т.е. для обратимого процесса трудно ска-зать, что будет исходным вещес-твом, а что продуктом.Изменение во времени:
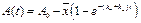
 (6) (6)
 (7) (7)
(6), (7) – кинетические кривые.Т. о., для обратимых химических процессов, как исходное вещес-тво, так и продукт ведут себя по-добно соответствующим вещес-твам для реакции 1-го порядка, но изменение во времени происходит в соответствии с константой  .По экспериментальным данным можно определить конст-анту прямой .По экспериментальным данным можно определить конст-анту прямой 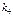 и обратной реа-кции и обратной реа-кции  , если результаты экспе-римента обработать в переменных , если результаты экспе-римента обработать в переменных
 Согласно (5’) Согласно (5’)
 , ,
x можно измерить.(рис20)
Когда система приходит в равно-весие:  , следовательно, найдем , следовательно, найдем 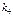 и и  .Аналогично обра-батываются результаты более вы-соких порядков. .Аналогично обра-батываются результаты более вы-соких порядков.
12. Метод квазистационарных концентраций. Формализм ме-тода.В ряде случаев получить то-чное решение кинетических урав-нений не удается. Возможна такая ситуация, что точное решение по-лучено, но использовать его для анализа невозможно, тогда испо-льзуются приближенные методы решения. В частности, в химичес-кой кинетике широко распростра-нен метод квазистационарных ко-нцентраций. Рассмотрим форма-льную сторону метода на примере образования бромистого водоро-да:
 ,Однако экспе-римент показывает другую кине-тическую скорость: ,Однако экспе-римент показывает другую кине-тическую скорость:
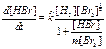 ,(*)т. е. ско-рость зависит еще и от продукта. Все это указывает на сложный ме-ханизм химического процесса. Он проходит в 5 стадий: ,(*)т. е. ско-рость зависит еще и от продукта. Все это указывает на сложный ме-ханизм химического процесса. Он проходит в 5 стадий:
1) 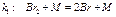
2) 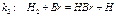
3) 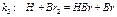
4) 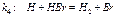
5) 
(Реакции 1 и 5, а также 2 и 4 вза-имообратные) Если определять скорость образования продукта по данному механизму, то получим
 (1)Скорость образования проду-кта зависит от концентраций про-межуточных продуктов. (1)Скорость образования проду-кта зависит от концентраций про-межуточных продуктов.
 (2) (2)
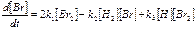  (3) (3)
 , ,  , тогда , тогда
 (2’) (2’)
 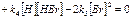 (3’) (3’)
Даже если считать, что концент-рации исходных веществ H2 и Br2 не меняются, то все равно получа-ется сложная система, которую сложно разрешить. Для данной системы используется приближе-ние. Дело в том, что промежу-точные продукты H и Br очень активны, поэтому в ходе химии-ческого процесса они сразу всту-пают во взаимодействие распада, и их концентрация на протяжении всего процесса очень мала, сле-довательно, ее можно считать по-стоянной. Такое состояние назы-вается квазистационарным сос-тоянием. Концентрации H и Br будут меняться только за счет изменения концентрации исход-ных веществ. Спустя небольшой промежуток времени в реагирую-щей системе устанавливается ква-зистационарное состояние, поэто-му эти концентрации можно най-ти. Решаем (2) и (3), сложим (2’) и (3’):  . .
Это уравнение соответствует хи-мическому равновесию 1-ой и
5-ой стадий, следовательно
 .Концентрацию во-дорода можно найти из (2’), под-ставим (4) в (2’): .Концентрацию во-дорода можно найти из (2’), под-ставим (4) в (2’):
 . (5) . (5)
Необходимо получить  , ,
т. е. как изменяется концентрация продукта. Для этого в (1) под-ставляем [H], [Br] и используем (2). Из (2’):
 ,. ,. 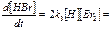   .(6)Получили выражение (6) для скорости образования продукта, которое качественно согласуется с экспе-риментальными данными по этой величине, т. е. с (*).Это качест-венное согласование зависимости скорости реакции от концент-раций .(6)Получили выражение (6) для скорости образования продукта, которое качественно согласуется с экспе-риментальными данными по этой величине, т. е. с (*).Это качест-венное согласование зависимости скорости реакции от концент-раций  указы-вает на правильность сделанных допущений, положенных в основу метода.Как видно из (6) фор-мальные экспериментальные па-раметры указы-вает на правильность сделанных допущений, положенных в основу метода.Как видно из (6) фор-мальные экспериментальные па-раметры 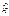 и m зависят от всех скоростей стадий процесса: k1, k2, k3, k4 и k5. Математическую осно-ву метода квазистационарных ко-нцентраций составляет асимпто-тический характер данной задачи, который лучше прослеживается по системе: и m зависят от всех скоростей стадий процесса: k1, k2, k3, k4 и k5. Математическую осно-ву метода квазистационарных ко-нцентраций составляет асимпто-тический характер данной задачи, который лучше прослеживается по системе:  , ,  , ε<<1. , ε<<1.
Если x, y – искомые функции, а t – независимая переменная, то
 , ,  . Все величины по-рядка единицы. Если f¹0, то f/ε>>φ, т. е. скорость изменения y будет бесконечно большой при ε®0, по сравнению со скоростью изменения x. Поэтому, вначале быстро изменяется y, а x прак-тически не изменяется. Так будет до тех пор, пока f не станет нулем. При f=0 y не меняется. Меняется медленно x, до тех пор, пока f¹0, тогда опять происходит быстрое изменение y, а x почти не изменяется и опять f=0, и т. д. . Все величины по-рядка единицы. Если f¹0, то f/ε>>φ, т. е. скорость изменения y будет бесконечно большой при ε®0, по сравнению со скоростью изменения x. Поэтому, вначале быстро изменяется y, а x прак-тически не изменяется. Так будет до тех пор, пока f не станет нулем. При f=0 y не меняется. Меняется медленно x, до тех пор, пока f¹0, тогда опять происходит быстрое изменение y, а x почти не изменяется и опять f=0, и т. д.
Не нашли, что искали? Воспользуйтесь поиском по сайту:
©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 ,
, (зависит от концент-рации промежуточного продукта)(1) (1)
(зависит от концент-рации промежуточного продукта)(1) (1)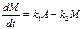 (зависит от конце-нтрации исходного вещества)(2) (2)
(зависит от конце-нтрации исходного вещества)(2) (2) (3)
(3) ,
,  .
. ,
,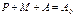 , (4)
, (4) , (4’)т.о. продукт можно найти, если знать концен-трации A и M. Чтобы из (2) найти M, необходимо найти A, для этого решим уравнение (3):
, (4’)т.о. продукт можно найти, если знать концен-трации A и M. Чтобы из (2) найти M, необходимо найти A, для этого решим уравнение (3):  . (5)
. (5)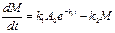
 .(k1≠k)
.(k1≠k) .(6)
.(6) (7).Таким образом, получены кинетические кривые для всех веществ (A, M, P), для случая
(7).Таким образом, получены кинетические кривые для всех веществ (A, M, P), для случая  .Рассмотрим особый случай k1=k2=k. Тогда решение можно по-лучить из (5) и (6). В (6) неопре-деленность раскроем по правилу Лапиталя:
.Рассмотрим особый случай k1=k2=k. Тогда решение можно по-лучить из (5) и (6). В (6) неопре-деленность раскроем по правилу Лапиталя:
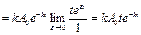
 . (6’)
. (6’)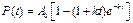 . (7’)
. (7’) , (когда
, (когда  порядка
порядка  ). (рис12)
). (рис12) ,
, близко к
близко к  , соотве-тственно
, соотве-тственно  – среднее время жизни по исходному веществу
– среднее время жизни по исходному веществу ,
, .
. .
. и
и  зависят от со-отношения
зависят от со-отношения  и
и 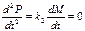
 , где
, где  – время, когда ко-нцентрация промежуточного про-дукта максимальна.
– время, когда ко-нцентрация промежуточного про-дукта максимальна.  , при
, при  ;
;  , при
, при  .
. (нем-ного ниже) Рассмотрим два преде-льных слу-чая: 1.k1>>k2
(нем-ного ниже) Рассмотрим два преде-льных слу-чая: 1.k1>>k2  ,
,

 , следовательно, в преде-льном случае M ведет себя как исходное вещество. (рис14).
, следовательно, в преде-льном случае M ведет себя как исходное вещество. (рис14).

 Т. е. проме-жуточный продукт M в системе будет находиться в малых коли-чествах, в течение всего процесса, т. к.
Т. е. проме-жуточный продукт M в системе будет находиться в малых коли-чествах, в течение всего процесса, т. к.  . Также в системе быстро устанавливается равно-весие между концентрацией исхо-дного вещества и промежу-точного продукта. Говорят, что M(t) будет находиться в квазиста-ционарном состоянии, т. е. его из-менение происходит только бла-годаря изменению A(t). Эти осо-бенности связаны с большой ак-тивностью M.(рис15). Сначала идет установление процесса,
. Также в системе быстро устанавливается равно-весие между концентрацией исхо-дного вещества и промежу-точного продукта. Говорят, что M(t) будет находиться в квазиста-ционарном состоянии, т. е. его из-менение происходит только бла-годаря изменению A(t). Эти осо-бенности связаны с большой ак-тивностью M.(рис15). Сначала идет установление процесса,  смещено к началу процесса. На таких особенностях основан ме-тод квазистационарных концент-раций. При таком соотношении констант ведущей стадией проце-сса является более медленная стадия (первая), она тормозит весь процесс, следовательно, оп-ределяет его. Для последователь-ных реакций ведущей стадией процесса является самая медле-нная.
смещено к началу процесса. На таких особенностях основан ме-тод квазистационарных концент-раций. При таком соотношении констант ведущей стадией проце-сса является более медленная стадия (первая), она тормозит весь процесс, следовательно, оп-ределяет его. Для последователь-ных реакций ведущей стадией процесса является самая медле-нная.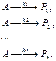
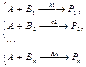
 , n-го порядка.
, n-го порядка.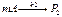 , m-го порядка.Тогда скорость образования продуктов согласно закону действующих масс:
, m-го порядка.Тогда скорость образования продуктов согласно закону действующих масс: Разделим первое уравнение на второе, получим:
Разделим первое уравнение на второе, получим:  .Т. е. образование продуктов будет проходить в строгой пропорции.Если n=m, то получаем наиболее простой слу-чай:
.Т. е. образование продуктов будет проходить в строгой пропорции.Если n=m, то получаем наиболее простой слу-чай:  ,
, - начальные концентрации. То есть, концентрации продуктов пропор-циональны соответствующим ко-нстантам скоростей.Если
- начальные концентрации. То есть, концентрации продуктов пропор-циональны соответствующим ко-нстантам скоростей.Если  , то
, то  .Вывод: ведущей стадией параллельных реакций является наиболее быстрая, по ней будет проходить основное преобразование исходного вещес-тва. Для выяснения характера ки-нетической кривой, рассмотрим схему (1) – параллельные реакции 1-го порядка. Выпишем диффе-ренциальные уравнения, опреде-ляющие изменение концентраций веществ:
.Вывод: ведущей стадией параллельных реакций является наиболее быстрая, по ней будет проходить основное преобразование исходного вещес-тва. Для выяснения характера ки-нетической кривой, рассмотрим схему (1) – параллельные реакции 1-го порядка. Выпишем диффе-ренциальные уравнения, опреде-ляющие изменение концентраций веществ: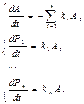
 ,
,  ,
,  .
. .Интегрируем с учетом начальных условий:
.Интегрируем с учетом начальных условий: 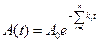
 .Скорость прохожден-ия параллельных реакций больше, чем скорость самой быстрой из реакций, входящих в неё. Изме-нение i-го продукта:
.Скорость прохожден-ия параллельных реакций больше, чем скорость самой быстрой из реакций, входящих в неё. Изме-нение i-го продукта: 
 ,
, ,т.е.
,т.е.  .Кинетическая кри-вая для P:
.Кинетическая кри-вая для P:  .Из последней формулы видно, что продукты образуются в строгой пропорции, определяемой их кон-стантой. В соответствии с этими константами будут находиться продукты после завершения хи-мического процесса.
.Из последней формулы видно, что продукты образуются в строгой пропорции, определяемой их кон-стантой. В соответствии с этими константами будут находиться продукты после завершения хи-мического процесса.  ,
,  .В конечном состоя-нии:
.В конечном состоя-нии: 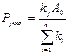 .Две реакции: P1k, P2k – конечные концентра-ции.
.Две реакции: P1k, P2k – конечные концентра-ции. 
 .(рис16)
.(рис16) По A ре-акция параллельная, по M реакция последовательна
По A ре-акция параллельная, по M реакция последовательна  (1)
(1)  ,(2
,(2  (3)Начальные условия:
(3)Начальные условия:  (отсутствуют в на-чальные момент).
(отсутствуют в на-чальные момент).  ,
, 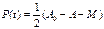 Разделим (1) на (2):
Разделим (1) на (2):
 ,
,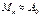
 (или очень мало)2. k1<<k2 Будет проя-вляться свойство последователь-ных реакций, поскольку вторая реакция не может быть реалиизо-вана без вещества M. Поэтому ве-дущей стадией будет являться первая реакция – самая медлен-ная. Первая реакция образует про-межуточный продукт M, и он с большой скоростью перерабаты-вается в P. Поэтому активный промежуточный продукт M в сис-теме будет находиться в малых количествах, в пропорции:
(или очень мало)2. k1<<k2 Будет проя-вляться свойство последователь-ных реакций, поскольку вторая реакция не может быть реалиизо-вана без вещества M. Поэтому ве-дущей стадией будет являться первая реакция – самая медлен-ная. Первая реакция образует про-межуточный продукт M, и он с большой скоростью перерабаты-вается в P. Поэтому активный промежуточный продукт M в сис-теме будет находиться в малых количествах, в пропорции:  ,т. е. в квазистаци-онарном состоянии. Только в на-чале процесса, пока будет прои-сходить установление квазистаци-онарного состояния M(t) будет от-личаться от данного выражения.
,т. е. в квазистаци-онарном состоянии. Только в на-чале процесса, пока будет прои-сходить установление квазистаци-онарного состояния M(t) будет от-личаться от данного выражения. Вывод: для по-следовательно-параллельных ре-акций, в зависимости от соотно-шения констант, могут проявлять-ся свойства как последовательн-ых, так и параллельных реакций.
Вывод: для по-следовательно-параллельных ре-акций, в зависимости от соотно-шения констант, могут проявлять-ся свойства как последовательн-ых, так и параллельных реакций. , A переходит в продукт P двумя путями: с константой скорости
, A переходит в продукт P двумя путями: с константой скорости  Скорость простой реакции
Скорость простой реакции  Скорость авто-каталитической реакции
Скорость авто-каталитической реакции 
 , (1)
, (1) .(2) Начальные условия:
.(2) Начальные условия:  .(3) Выделим первый интеграл, сло-жим (1) и (2):
.(3) Выделим первый интеграл, сло-жим (1) и (2):
 (4).Т. о. продукт мож-но определить через концентра-цию исходного вещества, (4) – закон сохранения массы вещес-тва.Перейдем к безразмерным переменным, глубина превраще-ния:
(4).Т. о. продукт мож-но определить через концентра-цию исходного вещества, (4) – закон сохранения массы вещес-тва.Перейдем к безразмерным переменным, глубина превраще-ния: , следова-тельно
, следова-тельно  .Используем уравнение (1) для нахождения η:
.Используем уравнение (1) для нахождения η: , где
, где  – масштабное время,
– масштабное время, 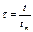 – безразмерное время.
– безразмерное время. , пусть для удобства
, пусть для удобства  .В качестве масштабного времени используем характерное время автокаталитической реакции.
.В качестве масштабного времени используем характерное время автокаталитической реакции. 
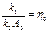
 (5)
(5)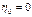 , то химический процесс начаться не может, пос-кольку начальная скорость у него будет равна нулю:
, то химический процесс начаться не может, пос-кольку начальная скорость у него будет равна нулю: .Т. о. параметр автокаталитичности оп-ределяет исходную (безразмерн-ую в данном случае) скорость реа-кции. Эта величина может быть отлична от 0 по двум причинам. Если
.Т. о. параметр автокаталитичности оп-ределяет исходную (безразмерн-ую в данном случае) скорость реа-кции. Эта величина может быть отлична от 0 по двум причинам. Если  , то
, то 

 .
.  ,
, .
.  Чтобы исходная скорость не равнялась нулю, надо, чтобы
Чтобы исходная скорость не равнялась нулю, надо, чтобы  , и начинает про-цесс эта простая реакция (играет роль затравки).Если в системе нет параллельной простой реакции, то чтобы начался процесс, необходи-мо присутствие хотя бы малого количества продукта реакции
, и начинает про-цесс эта простая реакция (играет роль затравки).Если в системе нет параллельной простой реакции, то чтобы начался процесс, необходи-мо присутствие хотя бы малого количества продукта реакции 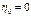 ,
,  . Продукт добавля-ют в систему для начала процесса. Можно сделать другое обезразме-ривание с выбором h, тогда (5) примет иной вид. Рассмотрим за-кономерности автокаталитическ-ой реакции согласно задаче (5). Рассмотрим, как меняется скоро-сть автокаталитической реакции в ходе химического процесса. Без-размерная скорость
. Продукт добавля-ют в систему для начала процесса. Можно сделать другое обезразме-ривание с выбором h, тогда (5) примет иной вид. Рассмотрим за-кономерности автокаталитическ-ой реакции согласно задаче (5). Рассмотрим, как меняется скоро-сть автокаталитической реакции в ходе химического процесса. Без-размерная скорость ,0≤η≤1Рассмотрим зависимость
,0≤η≤1Рассмотрим зависимость  :
: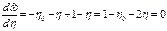 ,
, получаем точку экстремума.
получаем точку экстремума.  точка максимума.
точка максимума. в точке максимума:
в точке максимума:
 .
. , если
, если  .(рис17)Т. о. максимум скорости автокатали-тической реакции будет реали-зовываться в период химического процесса, если только параметр автокаталитичности η0<1. Иначе скорость
.(рис17)Т. о. максимум скорости автокатали-тической реакции будет реали-зовываться в период химического процесса, если только параметр автокаталитичности η0<1. Иначе скорость  на промежутке [0,1] будет монотонно падать, также как в случае простой реакции. Обычно для автокаталитических реакций
на промежутке [0,1] будет монотонно падать, также как в случае простой реакции. Обычно для автокаталитических реакций  .Обычно определяют не сам скорость хи-мической реакции, а ее отноше-ние к начальной скорости (во ско-лько раз увеличилась, или умень-шилась скорость по отношению к начальной скорости):
.Обычно определяют не сам скорость хи-мической реакции, а ее отноше-ние к начальной скорости (во ско-лько раз увеличилась, или умень-шилась скорость по отношению к начальной скорости): ;Максимум этого значения
;Максимум этого значения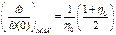
 , тем больше будет ускоре-ние химического процесса.(рис18)
, тем больше будет ускоре-ние химического процесса.(рис18) ).Если
).Если  или
или  , то самоускорения нет, и реакция ведет себя как простая.
, то самоускорения нет, и реакция ведет себя как простая.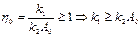 ,т. е. скорость простой реакции больше скорости автокаталитической и она является определяющей. Ра-ссмотрим кинетическую кривую автокаталитической реакции. Для этого проинтегрируем (5). Разделяем переменные:
,т. е. скорость простой реакции больше скорости автокаталитической и она является определяющей. Ра-ссмотрим кинетическую кривую автокаталитической реакции. Для этого проинтегрируем (5). Разделяем переменные: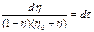 ,
, ,
, ,
, , тогда
, тогда (6)
(6) (6’)
(6’)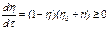
 , когда
, когда  .Т. о. кинетическая кривая имеет точку перегиба при
.Т. о. кинетическая кривая имеет точку перегиба при  , когда достигается максимум ско-рости автокаталитической реак-ции (рис19).
, когда достигается максимум ско-рости автокаталитической реак-ции (рис19). 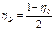
 :
: .Чем меньше
.Чем меньше  , тем больше
, тем больше  (только в безразмерном виде, т. к.
(только в безразмерном виде, т. к.  боль-ше, то время достижения
боль-ше, то время достижения  будет уменьшаться.Если
будет уменьшаться.Если  , то полу-чается кривая
, то полу-чается кривая  , точка перегиба совпадает с нулем, S-формы нет, и кинетическая кривая такая же, как для простой реакции 1-го порядка.
, точка перегиба совпадает с нулем, S-формы нет, и кинетическая кривая такая же, как для простой реакции 1-го порядка. , химический процесс дли-тельное время практически не идет (идет автокаталитическое самоускорение). При достижении некоторой величины η автоката-литическое ускорение становится существенным, и происходит разгон автокаталитической реак-ции, скорость становится больш-ой и химический процесс прохо-дит быстро. Экспериментаторы, тот промежуток времени, когда процесс почти не идет, назвали периодом индукции. Понятие пе-риода индукции является услов-ным, поскольку в зависимости от точности приборов, измеренное время появления продукта будет различно. Поэтому теоретически предложили в качестве периода индукции использовать
, химический процесс дли-тельное время практически не идет (идет автокаталитическое самоускорение). При достижении некоторой величины η автоката-литическое ускорение становится существенным, и происходит разгон автокаталитической реак-ции, скорость становится больш-ой и химический процесс прохо-дит быстро. Экспериментаторы, тот промежуток времени, когда процесс почти не идет, назвали периодом индукции. Понятие пе-риода индукции является услов-ным, поскольку в зависимости от точности приборов, измеренное время появления продукта будет различно. Поэтому теоретически предложили в качестве периода индукции использовать  .
. ,
,  – начало разгона (τm и τp почти равны).Рассмотрим случай
– начало разгона (τm и τp почти равны).Рассмотрим случай  , с периодом полупревра щения:
, с периодом полупревра щения:  .Если реакция простая, то
.Если реакция простая, то  , следовате-льно, по определению
, следовате-льно, по определению  .Реакция автокатали-тичная и
.Реакция автокатали-тичная и  ,
, .
.
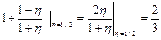
 ,и если параллель-но идет простая реакция порядка n, то ее скорость
,и если параллель-но идет простая реакция порядка n, то ее скорость 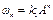 ,Тогда дифференциальное уравнение им-еет вид
,Тогда дифференциальное уравнение им-еет вид .Приведем задачу к безразмерному виду, вводя
.Приведем задачу к безразмерному виду, вводя  , получим уравне-ние
, получим уравне-ние  .Здесь параметр автокаталитичности и
.Здесь параметр автокаталитичности и 
 Примеры: Большинство автокаталити-ческих реакций протекает в жид-кой фазе. Впервые было получено Освальдом в 1883 году, при oму-лении метилацетата CH3COOCH3
Примеры: Большинство автокаталити-ческих реакций протекает в жид-кой фазе. Впервые было получено Освальдом в 1883 году, при oму-лении метилацетата CH3COOCH3 ,Сначала эксп-ериментально, потом теоретичес-ки.Пример газофазной реакции: термическая диссоциация водоро-да.
,Сначала эксп-ериментально, потом теоретичес-ки.Пример газофазной реакции: термическая диссоциация водоро-да. ,M – любая частица, например в аргоне Ar
,M – любая частица, например в аргоне Ar
 – уравнение цепн-ых реакций (Семенов).Многие взрывчатые вещества при низкой температуре реагируют по автока-талитическому механизму (тетрил η0=0,175). В зависимости от тем-пературы, механизм химической реакции может быть различным.
– уравнение цепн-ых реакций (Семенов).Многие взрывчатые вещества при низкой температуре реагируют по автока-талитическому механизму (тетрил η0=0,175). В зависимости от тем-пературы, механизм химической реакции может быть различным.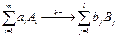 ,
,  – стехиометрические коэффициен-ты. Поскольку реакция простая, то, согласно уравнению, можно составить пропорцию по измене-нию концентраций участвующих веществ:
– стехиометрические коэффициен-ты. Поскольку реакция простая, то, согласно уравнению, можно составить пропорцию по измене-нию концентраций участвующих веществ:  .Получаем m+l равенств. Продиффере-нцируем:
.Получаем m+l равенств. Продиффере-нцируем:  . Согласно закону действующих масс
. Согласно закону действующих масс  (произведение по всем i).Де-Донде предложил для исследования процесса Рас-смотреть величину x, которому равна первая пропорция (1). x ха-рактеризует ход процесса, опреде-ляя насколько глубоко прошла ре-акция. В начале процесса x=0, а далее x будет возрастать. В отли-чие от глубины превращения x яв-ляется размерной величиной и соответствует размерности конце-нтрации. Зная x, можно найти все A, и все B.
(произведение по всем i).Де-Донде предложил для исследования процесса Рас-смотреть величину x, которому равна первая пропорция (1). x ха-рактеризует ход процесса, опреде-ляя насколько глубоко прошла ре-акция. В начале процесса x=0, а далее x будет возрастать. В отли-чие от глубины превращения x яв-ляется размерной величиной и соответствует размерности конце-нтрации. Зная x, можно найти все A, и все B. Уравнение для x найдем из (2), подставив
Уравнение для x найдем из (2), подставив  или
или 
 .Реакция может идти как в прямом, так и в обратном направлении. Только при различных темпера-турах состояние химического рав-новесия может быть смещено либо в сторону продуктов, либо в сторону исходных веществ. То ес-ть, если при химическом равнове-сии продуктов почти нет, то гово-рят, что реакция не идет (хими-ческое равновесие смещено в сто-рону исходных веществ). Если при химическом равновесии ис-ходных веществ практически нет, то говорят, что химическая реак-ция идет до конца (химическое равновесие смещено в сторону продуктов).В зависимости от температуры, химическое равно-весие может изменяться, и при определенных температурах, в состоянии равновесия, в смесях могут быть и исходные вещества, и продукты. Рассмотрим законно-мерности химического процесса:
.Реакция может идти как в прямом, так и в обратном направлении. Только при различных темпера-турах состояние химического рав-новесия может быть смещено либо в сторону продуктов, либо в сторону исходных веществ. То ес-ть, если при химическом равнове-сии продуктов почти нет, то гово-рят, что реакция не идет (хими-ческое равновесие смещено в сто-рону исходных веществ). Если при химическом равновесии ис-ходных веществ практически нет, то говорят, что химическая реак-ция идет до конца (химическое равновесие смещено в сторону продуктов).В зависимости от температуры, химическое равно-весие может изменяться, и при определенных температурах, в состоянии равновесия, в смесях могут быть и исходные вещества, и продукты. Рассмотрим законно-мерности химического процесса: – в обрат-ном направлении.Скорость хи-мического процесса ω, будет оп-ределяться суммой скоростей, с учетом направления:
– в обрат-ном направлении.Скорость хи-мического процесса ω, будет оп-ределяться суммой скоростей, с учетом направления:  . Если наступит химическое равно-весие, то суммарная скорость ω=0, тогда:
. Если наступит химическое равно-весие, то суммарная скорость ω=0, тогда: (4)
(4) 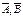 – концентрации, в состоянии хими-ческого равновесия. Равновесные процессы изучаются в равновесной термодинамике. Термодинамичес-кая константа равновесия
– концентрации, в состоянии хими-ческого равновесия. Равновесные процессы изучаются в равновесной термодинамике. Термодинамичес-кая константа равновесия .Согласно (4), конст-анта
.Согласно (4), конст-анта  .Т. о., если реакция простая, то её константа равнове-сия равна отношению констант скоростей прямой и обратной реа-кции. Кинетические закономерно-сти обратимого процесса удобно определять через x. Уравнение д-ля x определяется также из (2), но вместо ω, подставляется ω с уче-том прямой и обратной реакции. Для x получаем уравнение:
.Т. о., если реакция простая, то её константа равнове-сия равна отношению констант скоростей прямой и обратной реа-кции. Кинетические закономерно-сти обратимого процесса удобно определять через x. Уравнение д-ля x определяется также из (2), но вместо ω, подставляется ω с уче-том прямой и обратной реакции. Для x получаем уравнение: 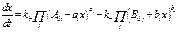
 Тогда урав-нение (3‘) принимает вид:
Тогда урав-нение (3‘) принимает вид: ,
, (3’’)
(3’’)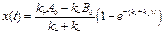 (5Разделим на
(5Разделим на  .
. (5’).
(5’). .
. .
. .Если подставить
.Если подставить  в выражения для A и B, то получим их равновесные значения:
в выражения для A и B, то получим их равновесные значения: (
( 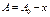 ,
,  )
)  ,
,  .
. , тогда B будет исходным веществом, A продуктом. Т.е. для обратимого процесса трудно ска-зать, что будет исходным вещес-твом, а что продуктом.Изменение во времени:
, тогда B будет исходным веществом, A продуктом. Т.е. для обратимого процесса трудно ска-зать, что будет исходным вещес-твом, а что продуктом.Изменение во времени: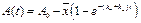
 (6)
(6) (7)
(7) .По экспериментальным данным можно определить конст-анту прямой
.По экспериментальным данным можно определить конст-анту прямой 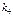 и обратной реа-кции
и обратной реа-кции  , если результаты экспе-римента обработать в переменных
, если результаты экспе-римента обработать в переменных Согласно (5’)
Согласно (5’) ,
, , следовательно, найдем
, следовательно, найдем  ,Однако экспе-римент показывает другую кине-тическую скорость:
,Однако экспе-римент показывает другую кине-тическую скорость: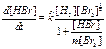 ,(*)т. е. ско-рость зависит еще и от продукта. Все это указывает на сложный ме-ханизм химического процесса. Он проходит в 5 стадий:
,(*)т. е. ско-рость зависит еще и от продукта. Все это указывает на сложный ме-ханизм химического процесса. Он проходит в 5 стадий: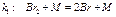
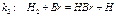
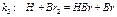
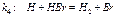

 (1)Скорость образования проду-кта зависит от концентраций про-межуточных продуктов.
(1)Скорость образования проду-кта зависит от концентраций про-межуточных продуктов. (2)
(2)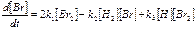
 (3)
(3) ,
,  , тогда
, тогда (2’)
(2’)
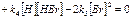 (3’)
(3’) .
. .Концентрацию во-дорода можно найти из (2’), под-ставим (4) в (2’):
.Концентрацию во-дорода можно найти из (2’), под-ставим (4) в (2’): . (5)
. (5) ,
, ,.
,. 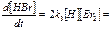

 .(6)Получили выражение (6) для скорости образования продукта, которое качественно согласуется с экспе-риментальными данными по этой величине, т. е. с (*).Это качест-венное согласование зависимости скорости реакции от концент-раций
.(6)Получили выражение (6) для скорости образования продукта, которое качественно согласуется с экспе-риментальными данными по этой величине, т. е. с (*).Это качест-венное согласование зависимости скорости реакции от концент-раций  указы-вает на правильность сделанных допущений, положенных в основу метода.Как видно из (6) фор-мальные экспериментальные па-раметры
указы-вает на правильность сделанных допущений, положенных в основу метода.Как видно из (6) фор-мальные экспериментальные па-раметры 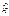 и m зависят от всех скоростей стадий процесса: k1, k2, k3, k4 и k5. Математическую осно-ву метода квазистационарных ко-нцентраций составляет асимпто-тический характер данной задачи, который лучше прослеживается по системе:
и m зависят от всех скоростей стадий процесса: k1, k2, k3, k4 и k5. Математическую осно-ву метода квазистационарных ко-нцентраций составляет асимпто-тический характер данной задачи, который лучше прослеживается по системе:  ,
,  , ε<<1.
, ε<<1. ,
,  . Все величины по-рядка единицы. Если f¹0, то f/ε>>φ, т. е. скорость изменения y будет бесконечно большой при ε®0, по сравнению со скоростью изменения x. Поэтому, вначале быстро изменяется y, а x прак-тически не изменяется. Так будет до тех пор, пока f не станет нулем. При f=0 y не меняется. Меняется медленно x, до тех пор, пока f¹0, тогда опять происходит быстрое изменение y, а x почти не изменяется и опять f=0, и т. д.
. Все величины по-рядка единицы. Если f¹0, то f/ε>>φ, т. е. скорость изменения y будет бесконечно большой при ε®0, по сравнению со скоростью изменения x. Поэтому, вначале быстро изменяется y, а x прак-тически не изменяется. Так будет до тех пор, пока f не станет нулем. При f=0 y не меняется. Меняется медленно x, до тех пор, пока f¹0, тогда опять происходит быстрое изменение y, а x почти не изменяется и опять f=0, и т. д.