
|
|
Скорость простых химических превращений.Пусть имеется стехиометрии-чес-кое уравнение простой реак-ции: aA+bB+cC+…=pP+qQ+…(1) A,B,C – символы исходных веще-ств; P,Q – символы продуктов реакции; a, b, c, p, q – стехиометрические коэффициенты. В дальнейшем будем использо-вать соответствующие обозначе-ния для концентраций или масс соответствующих компонентов (концентрация А равна А, и т. д.). Стехиометрическое уравнение по-казывает, в какой пропорции из-меняются массы соответствую-щих компонентов, и т. к. реакция (1) простая, а стехиометрические коэффициенты указывают, в ка-кой пропорции изменяются (рас-ходуются) концентрации соотве-тствующих веществ, то согласно (1) можно составить пропорцию:
В (2) символом “0” обозначены концентрации соответствующих веществ в начальный момент времени, и вся реакция проходит при постоянном объеме, поэтому скорость реакции можно опре-делить по скорости изменения концентрации.
Согласно определению, для реак-ции при постоянном объеме, бу-дем иметь:
Исследование, проведенное Гиль-бертом и Ваге при T=const, пока-зало, что скорость простой реак-ции ω пропорциональна концент-рациям исходных веществ, в степени их стехиометрических ко-эффициентов. Этот закон, называется законом действующих масс, т. е. действуют массы исходных веще-ств. Коэффициент пропорцио-нальности k=k(T). Позже этот закон получил теоретическое обоснование исхо-дя из вероятностного подхода: Произведение Использование (3) для опреде-ления скорости по конкретным веществам удобно, поэтому это соотношение стали распрост-ранять и на сложные химические процессы. В этом случае испо-льзуют формальные константы, которые получают из экспе-римента. Скорость таких проце-ссов будет иметь вид: ω=k(T) φ(A, B,…, P, Q,…) (5) k(T) – константа скорости хими-ческой реакции, определяет зависимость скорости химической реакции от температуры. Функция φ(A, B,…,P, Q,…) – называется Кинетической функцией. Она определяет зависимость скорости химической реакции от концент-рации веществ, которые в ней участвуют, и данная зависимость может быть различной. Сюда мо-гут входить концентрации исход-ных веществ, продуктов а также промежуточных веществ. Функ-циональная зависимость может быть различной (логарифмиче-ской, дробной, и т. д.). Данная зависимость находится из эксперимента, хотя её можно определить, используя механизм химической реакции. Для простой реакции кинетическая функция имеет вид: Если из эксперимента получено, что φ зависит еще и от продуктов, и промежуточных веществ, или если степени концентраций исх-одных веществ дробные, то это указывает на сложный механизм химической реакции. При этом, если используют формулу (5), то говорят, что рассматривают формальную кинетику химичес-кого процесса, поскольку это со-ответствует эксперименту, и поз-воляет получать зависимости из-менения масс веществ (кинети-ческие зависимости) с использо-ванием формального подхода:
Для газофазных реакций общий порядок показывает степень зави-симости скорости химической реакции от давления:
где
В частности: 1)если реакция первого порядка, т. е. n=1, тогда - Для описания химических про-цессов, используется скорость хи-мической реакции вида (5), через которую по соотношению (3’) оп-ределяются скорости хим. реак-ции по конкретным веществам. - Для простых химических реак-ций выполняется закон действую-щих масс (4), в котором кинетиче-ская функция зависит только от произведения концентраций исхо-дных веществ в степенях их сте-хиометрических коэффициентов. §5. Кинетические закономерно-сти протекания простых химии-ческих реакций в изотермичес-ких условиях. T=const. Изучим зависимость поведения параметров системы в зависимос-ти от кинетической функции φ. Начнем с простых реакций. 1. Односторонние реакции 1-го порядка.Рассмотрим реакцию: и можно записать, как изменяют-ся исходные вещества и продукты реакции(a=p=1) Из системы (1), (2) можно получить первый интеграл:
(3), либо (3’) – первый интеграл системы (1), (2), он выражает закон сохранения массы вещества в системе.Чтобы найти A(t), надо решить (1), разделяя переменные, получим:
Из начальных условий – кинетическая кривая (зависи-мость) исходного вещества. По закону (4) изменяется кон-центрация исходного вещества в случае реакции 1-го порядка.Если (4) подставить в (3’), то получим кинетическую зависимость для продуктаP: Для описания процессов необхо-димо характерное время прохож-дения процесса. Поскольку в описании t=∞, то в качестве хара-ктерного времени часто использу-ется среднее время жизни хи-мического процесса: это время, в течение которого концентрация исходного вещества уменьшилась в e раз. Тогда из (4) имеем:
следовательно ln2≈0,693.Времена (5) и (6) близ-ки между собой, поэтому любое из них можно использовать в кА-честве характерного времени.Из (5) и (6) следует характерная осо-бенность реакции первого поряд-ка: характерные времена – полуп-ревращения или среднее время жизни зависят только от констан-ты химической реакции и не зави-сят от начальной концентрации исходного вещества. Таким обра-зом, для этих процессов важно знать k. Её часто определяют из эксперимента, с помощью получе-ния экспериментальной кинети-ческой кривой A(t). Результаты эксперимента обрабатываются в координатах 2. Простые реакции 2-го поряд-ка.
Вычтем (2) из (1):
Сложим(1)и(3): – 2-ой интеграл. То есть, концентрацию продукта можно будет определить, когда будет известна A(t).В (1) заменим B через А используя (4), получим: Разложив на простые дроби полу-чим Из (7), с учетом (4) можно найти A(t), которая представляет кине-тическую кривую для исходного вещества A. Рассмотрим частный случай ε=0. С математической точки зрения решение будет иметь качественно другой вид (7), который можно найти, используя правило Лапи-таля. С химической точки зрения этот случай интересен тем что 1).Либо два одинаковых вещества вступают в химическое взаимоде-йствие, с образованием продукта, как например, в случае термичес-кого разложения йодистого водо-рода: 2).Либо в реакцию вступают два различных вещества, но началь-ные концентрации у них равны:
с учетом начальных условий
Из (9) следует, что в случае реакции 2-го порядка характерное время зависит не только от k, но и от начальной концентрации A0. Используя кинетическую кривую (8) можно находить константу скорости с помощью эксперимен-тальных данных. Для этого испо-льзуется (8’), и результаты экспе-римента обрабатываются в коор-динатах Другой предельный случай ε>>A. Это означает, что
3. Реакции 3-го порядка
Аналогично для других веществ. Поскольку для таких систем также будут иметь место первые интегралы, то решение будет оп-ределять дифференциальное урав-нение для A. Рассмотрим случай, когда Характерное время реакции мож-но определить по времени полуп-ревращения:
4. Обобщение на реакцию n-го порядка.Если реакция протекает по схеме: Формально имеем реакцию n-го порядка. Получим кинетическую кривую
При n=1: При:-n>1: Таким образом, при любом n≥1 кинетическая кривая монотонно падает, асимптотически стремясь к 0. Наклон кривой зависит от порядка реакции. Характерное время реакции – время полупрев-ращения: С ростом n порядка реакции, степень зависимости характерно-го времени от начальной концен-трации, возрастает. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 (2)
(2)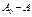 – расход (A<A0),
– расход (A<A0), 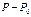 – образование (P>P0). Продифференцируем (2) по времени:
– образование (P>P0). Продифференцируем (2) по времени: (3)
(3) , где
, где  , и т. д.Т. е. для про-стой реакции скорости по разли-чным веществам связаны между собой через стехиометрические коэффициенты. Поэтому, согла-сно равенству (3), можно ввести понятие скорости химической реакции ω. Через эту общую скорость можно определить ско-рость этой реакции по конкре-тному веществу, используя соот-ветствующий стехиометрический коэффициент.
, и т. д.Т. е. для про-стой реакции скорости по разли-чным веществам связаны между собой через стехиометрические коэффициенты. Поэтому, согла-сно равенству (3), можно ввести понятие скорости химической реакции ω. Через эту общую скорость можно определить ско-рость этой реакции по конкре-тному веществу, используя соот-ветствующий стехиометрический коэффициент.  (3’)
(3’) (4)
(4) определяет вероятность встречи молекул в одной точке пространства.
определяет вероятность встречи молекул в одной точке пространства. .
. , где
, где  – порядки реак-ции по соответствующему вещес-тву. Общий порядок реакции:
– порядки реак-ции по соответствующему вещес-тву. Общий порядок реакции:  .
.
 ,
, – давление. Подставим в формулу для φ, получим:
– давление. Подставим в формулу для φ, получим: Размерность скорости химической реакции. Согласно определению или формуле (3):
Размерность скорости химической реакции. Согласно определению или формуле (3):  ,
,  Согласно (5):
Согласно (5):  ,
,  – для степенных законов. Для ко-нстанты скорости:
– для степенных законов. Для ко-нстанты скорости: – для степенной зависимости.
– для степенной зависимости. ,
,  ;2).если реакция вто-рого порядка (два исходных веще-ства),то:
;2).если реакция вто-рого порядка (два исходных веще-ства),то: 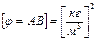 ,
,  ;Таким образом, имеем:
;Таким образом, имеем: ,тогда согласно закону действующих масс (4):
,тогда согласно закону действующих масс (4):  ,
, (1)
(1)  (2)Эти диффе-ренциальные уравнения опреде-ляют концентрацию вещества A и продукта P. Необходимо найти A(t) и P(t) (k=const, так как T=const). Для решения уравнения (1) и (2), и получения однозна-чного ответа, необходимы началь-ные условия (так как ДУ 1-го по-рядка, то для двух уравнений не-обходимо задать два начальных условия):
(2)Эти диффе-ренциальные уравнения опреде-ляют концентрацию вещества A и продукта P. Необходимо найти A(t) и P(t) (k=const, так как T=const). Для решения уравнения (1) и (2), и получения однозна-чного ответа, необходимы началь-ные условия (так как ДУ 1-го по-рядка, то для двух уравнений не-обходимо задать два начальных условия): Складывая эти два ура-внения, получим
Складывая эти два ура-внения, получим  .
.  ,(3)
,(3)  .(3’)
.(3’)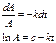
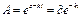
 , тогда
, тогда  (4)
(4)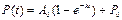 . (рис4) Т. о., процесс закончится лишь при t=∞ (все вещество перейдет в продукт). Поскольку чувствитель-ность измерительных приборов ограничена, то они наблюдают окончание процесса раньше. Од-нако это время не может служить временем окончания процесса, т. к. оно будет зависеть от прибора.
. (рис4) Т. о., процесс закончится лишь при t=∞ (все вещество перейдет в продукт). Поскольку чувствитель-ность измерительных приборов ограничена, то они наблюдают окончание процесса раньше. Од-нако это время не может служить временем окончания процесса, т. к. оно будет зависеть от прибора. ,следовательно
,следовательно  ,(5)т. е. среднее время жизни зависит от константы ско-рости. Также в качестве характер-ного времени используется время полураспада (полупревращени-я): это время, в течение которого концентрация исходного вещест-ва уменьшилась в два раза. Согла-сно (4):
,(5)т. е. среднее время жизни зависит от константы ско-рости. Также в качестве характер-ного времени используется время полураспада (полупревращени-я): это время, в течение которого концентрация исходного вещест-ва уменьшилась в два раза. Согла-сно (4):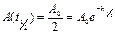 ,
,  ,
, .(6)
.(6) .Согласно (4) для простой реакции1-го по-рядка должно быть
.Согласно (4) для простой реакции1-го по-рядка должно быть  (4’).График (4’): (рис5 tga=k где α угол наклона прямой, построенной по эксперименталь-но полученным точкам по методу наименьших квадратов. Пример реакции 1-го порядка:реакция распада гексафенилэтана на два свободных радикала трифенил-метана
(4’).График (4’): (рис5 tga=k где α угол наклона прямой, построенной по эксперименталь-но полученным точкам по методу наименьших квадратов. Пример реакции 1-го порядка:реакция распада гексафенилэтана на два свободных радикала трифенил-метана 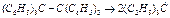
 Дифференциальные кинетические уравнения:
Дифференциальные кинетические уравнения: (1)
(1)  (2)
(2)  (3)Начальные условия
(3)Начальные условия  ,
,  ,
, 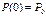 .
.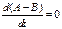
 , где
, где  ,
, (4) – 1-й интеграл.
(4) – 1-й интеграл.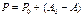 (5)
(5) (6)
(6)  ,
, .Интегрируем
.Интегрируем  Из началь-ных условий
Из началь-ных условий 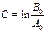 , получаем:
, получаем:  (7)
(7) , это означает, что:
, это означает, что: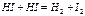 .
. . При t=0
. При t=0  – начальные концент-рации. Рассмотрим последний случай, тогда (6) принимает вид:
– начальные концент-рации. Рассмотрим последний случай, тогда (6) принимает вид: ,
, 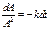 ,
,  ,
, , тогда
, тогда  , (8’)
, (8’)  (8)-кинетическая кри-вая. Так как B=A, то для В будем иметь эту же кривую.(рис6).В это-м случае также требуется харак-терное время реакции, т. к. мате-матически процесс заканчивается лишь при t=∞. В качестве харак-терного времени используется ли-бо среднее время жизни реакции, либо время полупревращения. Определим
(8)-кинетическая кри-вая. Так как B=A, то для В будем иметь эту же кривую.(рис6).В это-м случае также требуется харак-терное время реакции, т. к. мате-матически процесс заканчивается лишь при t=∞. В качестве харак-терного времени используется ли-бо среднее время жизни реакции, либо время полупревращения. Определим  из (8):
из (8):
 (9)
(9) (рис7).tga=k, где α – угол наклона прямой, постро-енной по методу наименьших ква-дратов с использованием получе-нных экспериментально точек.
(рис7).tga=k, где α – угол наклона прямой, постро-енной по методу наименьших ква-дратов с использованием получе-нных экспериментально точек.
 . То есть вещество B на-ходится в системе в избытке. В этом случае уравнение (6) можно преобразовать
. То есть вещество B на-ходится в системе в избытке. В этом случае уравнение (6) можно преобразовать 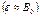 :
: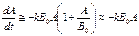 , т. к.
, т. к. 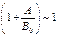 .Тогда формально мо-жно рассматривать уравнение:
.Тогда формально мо-жно рассматривать уравнение: ,т. е. получили урав-нение, как для случая реакции 1-го порядка. Говорят, имеет место формальное понижение по-рядка реакции. Формализм: поря-док реакции определяет степень зависимости от давления. Для ре-акции 1-го порядка
,т. е. получили урав-нение, как для случая реакции 1-го порядка. Говорят, имеет место формальное понижение по-рядка реакции. Формализм: поря-док реакции определяет степень зависимости от давления. Для ре-акции 1-го порядка 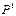 , для 2-го
, для 2-го  .ЗдесьA~P и
.ЗдесьA~P и 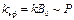 .По размерности kэф соответствует константе скорости k.
.По размерности kэф соответствует константе скорости k. .Запишем кинети-ческие дифференциальные урав-нения только для вещества A:
.Запишем кинети-ческие дифференциальные урав-нения только для вещества A: , если
, если  ;
;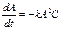 , если
, если  ;
; , если
, если  .
. домножим на -2, и с учетом начальных условий:
домножим на -2, и с учетом начальных условий:  ,получаем:
,получаем:  (10)Кинетическая кривая (10) также будет предста-влять монотонно-падающую кри-вую, которая при t→∞ асимпто-тически стремится к 0(рис8).
(10)Кинетическая кривая (10) также будет предста-влять монотонно-падающую кри-вую, которая при t→∞ асимпто-тически стремится к 0(рис8). (11)Зависимость от начальной концентрации усилилась. Аналогично выражает-ся среднее время жизни. И также как и в случае реакции 2-го поря-дка константу скорости можно получить экспериментально, об-работав результаты эксперимента в координатах
(11)Зависимость от начальной концентрации усилилась. Аналогично выражает-ся среднее время жизни. И также как и в случае реакции 2-го поря-дка константу скорости можно получить экспериментально, об-работав результаты эксперимента в координатах 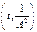 . Классичес-ким примером простой реакции 3-го порядка является реакция:
. Классичес-ким примером простой реакции 3-го порядка является реакция: –газофазная реак-ция ( проходит при высокой тем-пературе).
–газофазная реак-ция ( проходит при высокой тем-пературе).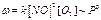 Чаще по меха-низму реакции 3-го порядка про-текают реакции между атомами и свободными радикалами.Простые реакции 4-го, 5-го, и более высо-кого порядка маловероятны. Там чаще реализуется сложный меха-низм, с образованием промежуто-чных продуктов.Реакция первого порядка называется мономоле-кулярной. Реакция второго поря-дка – бимолекулярной.Реакция третьего порядка – тримолекуля-рной. В случае реакции третьего порядка также возможно форма-льное понижение порядка реак-ции до второго, а затем до перво-го.
Чаще по меха-низму реакции 3-го порядка про-текают реакции между атомами и свободными радикалами.Простые реакции 4-го, 5-го, и более высо-кого порядка маловероятны. Там чаще реализуется сложный меха-низм, с образованием промежуто-чных продуктов.Реакция первого порядка называется мономоле-кулярной. Реакция второго поря-дка – бимолекулярной.Реакция третьего порядка – тримолекуля-рной. В случае реакции третьего порядка также возможно форма-льное понижение порядка реак-ции до второго, а затем до перво-го. ,(n веществ A образуют продукт P) , то уравне-ние для концентрации вещества A имеетвид
,(n веществ A образуют продукт P) , то уравне-ние для концентрации вещества A имеетвид  (12)
(12) ,
, , (n>1).
, (n>1). .
. .
. ,
,