
|
|
Создание новых форм объектовРассмотрим варианты создания нового объекта на основе прямоугольника и окружности. Сварить (из двух объектов создается один по общему внешнему контуру).
Рис. 5 Создание новых форм объектов Обрезать предполагает, что из нижнего объекта будет «отрезан» фрагмент, соответствующий заходящей на него части верхнего объекта. В результате этого преобразования получается два объекта – нижний подрезанный и верхний неизменный. Команда Пересечение позволяет получить объект, образованный пересечением объектов. В итоге из двух у нас получится три объекта – оба исходных и еще новый. Инструменты рисования кривых Инструмент Свободная рука Инструмент Свободная рука позволяет рисовать кривые произвольной формы. Существует два способа рисования. Первый заключается в том, чтобы нажать левую кнопку мыши и, не отпуская ее, перемещать указатель по странице документа. После того как кнопка будет отпущена, появится кривая, форма которой будет повторять траекторию указателя. Точность, с которой кривая соответствует траектории, задается в поле Ручное сглаживание, расположенном в правой части панели свойств. Второй способ позволяет рисовать прямые. Первый щелчок мыши задает начальную точку отрезка, второй – конечную. Инструмент Кривая Безье Каждый щелчок этим инструментом создает узел кривой Безье. Однократный щелчок приводит к созданию прямого узла. Если после щелчка не отпускать кнопку мыши, а переместить указатель, появятся направляющие угла.
Инструмент Живопись У инструмента Живопись пять режимов, позволяющих создавать необычные графические эффекты обводки. Выбрать один из режимов можно, активизировав инструмент Живопись и щелкнув на соответствующей кнопке в левой части панели свойств.
Инструмент Перо Рисование пером очень напоминает рисование инструментом Кривая Безье по принципу «узел за узлом». Для окончания работы с инструментом Перо нужно дважды щелкнуть левой кнопкой мыши. Если на панели свойств включен Режим просмотр, то в процессе рисования видно, как себя ведут создаваемые сегменты кривой. Помимо вышеперечисленных инструментов применяются следующие: · инструмент Полилиния; · инструмент Кривая по трем точкам; · инструмент Интерактивная соединительная линия; · инструмент размер.
Редактирование текста Corel Draw позволяет создавать текстовые объекты двух типов: нормальный текст (Paragraph) и артистический текст (Artistic). Артистический текст в основном служит для создания красивого оформления публикаций. Для создания объекта Artistic нужно нажать на пиктограмму на панели инструментов. При этом рамки текста не ограничены - достаточно один раз щелкнуть в любом месте экрана - и можно вводить текст. По мере набора границы объекта будут расширяться автоматически. Для ввода большого количества текста лучше использовать формат Paragraph. Для создания объекта Paragraph необходимо удержать данную пиктограмму на некоторое время и затем выбрать. При создании объекта нужно указать ту область на листе, в которой будет размещаться текст. При заполнении всей рамки текстом, он не будет выводиться на экран. Нужно либо расширить границы, либо перенести ту часть, которая не влезла, в другой объект Paragraph.
С объектом текста можно производить различные эффекты, используя команды из меню Effects: масштабирование, растягивание, сжатие, перекос, вращение. Как и любая программа, работающая по принципу WYSIWYG, Corel Draw наглядно отображает все изменения текста на экране. Редактор позволяет использовать все установленные шрифты Windows типов True Type и Post Script 1. Рассмотрим основные операции, которые можно выполнять с текстом в Corel Draw. Для форматирования вида самого текста используется меню Text. Ниже дано описание его пунктов.
Text Roll-Up Основные параметры текста: используемый шрифт, его размер, выравнивание строк (слева, справа, по центру, по ширине). Из этого меню можно попасть в другие меню для установки более специализированных параметров.
Character При выборе этого пункта выводится меню, в котором пользователь может изменить используемый шрифт, размер, стиль символов (подчеркнутый, перечеркнутый, нижний, верхний регистр), расстояние между символами, словами и строками, выравнивание строк (слева, справа, по центру, по ширине). Линия подчеркивания может быть одинарной или двойной, тонкой или толстой.
Paragraph Только для объекта Paragraph. В этом меню можно изменять параметры параграфа текста, как то: расстояние между строками, словами и символами, границы параграфа, отступы слева и справа, позиции табуляции. Можно вставлять символы из специальных художественных шрифтов (животные, продукты, музыкальные символы и т.п.).
Frame Только для объекта Paragraph. Позволяет выводить текст в формате газеты, т.е. колонками. Число колонок - от 1 до 8. Можно задать ширину каждой колонки. При вводе текст автоматически переносится в следующую колонку, когда достигается нижняя граница объекта.
Fit Text To Path Данная команда объединяет текст с каким либо объектом таким образом, что текст огибает данный объект. Corel Draw позволяет выбирать различные виды наложения текста. Например, выстроить “заборчиком” по периметру. Можно выбрать, с какого края писать текст: сверху, снизу, слева или справа.
Align To Baseline Выравнивает текст по базовой линии.
Straighten Text Выравнивает текст по базовой линии и приводит формат всех символов (изгиб, смещение) к обычному. С текстом можно производить те же операции растяжения, сжатия, вращения и сдвига, что и с обычным объектом. Для этого нужно в меню Effects выбрать пункт Transform Roll-Up (в этом случае появится меню), или просто щелкнуть мышью на объекте.
Отражение (Mirror) Эта функция позволяет перевернуть текст слева направо или сверху вниз. Следует отметить, что все-таки механизм работы с большими объемами текста в Corel Draw очень несовершенен. Пользователь, знакомый с мощными текстовыми процессорами или издательскими системами для Windows, сразу заметит неудобство интерфейса Corel Draw. Часто приходится переключать вид курсора для работы с текстом и с объектами, по несколько раз переопределять стиль текста. Сложно сделана работа с параграфами. Нет многих полезных, а зачастую и необходимых функций редактирования. С другой стороны, если учитывать, для каких целей создан данный пакет, то поддержка работы с текстом сделана хорошо.
12. Алгоритм Брезенхэма Алгоритм Брезенхэма - это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэм компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка. Более подробно про растровые алгоритмы, к которым относится данный алгоритм смотри в вопросе №13.
Алгоритм: Отрезок проводится между двумя точками — (x0,y0) и (x1,y1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x1 − x0 превосходит вертикальное y1 − y0, т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x0 и x1, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y). Общая формула линии между двумя точками:
Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения: Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y0 и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона
которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1. Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y)рисует точку, а abs возвращает абсолютную величину числа: function line(x0, x1, y0, y1) int deltax := abs(x1 - x0) int deltay := abs(y1 - y0) real error := 0 real deltaerr := deltay / deltax int y := y0 for x from x0 to x1 plot(x,y) error := error + deltaerr if error >= 0.5 y := y + 1 error := error - 1.0 Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код: function line(x0, x1, y0, y1) int deltax := abs(x1 - x0) int deltay := abs(y1 - y0) int error := 0 int deltaerr := deltay int y := y0 for x from x0 to x1 plot(x,y) error := error + deltaerr if 2 * error >= deltax y := y + 1 error := error - deltax Умножение на 2 для целых чисел реализуется битовым сдвигом влево. Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца. Из презентации: Отрезок от A(xa, ya) до B(xb, yb) 0 £ yb- ya £ xb- xa, k=(yb- ya) / (xb- xa) y = ya+ k (x – xa) procedure line(xa,ya,xb,yb:integer); var k,y : double; begin k:=(yb-ya)/(xb-xa); y:=ya; for i:=xa to xb do begin put(x,round(y)); y:=y+k end; end;
13.Алгоритм Брезенхема рисования окружности. Растровые алгоритмы Большинство графических устройств являются растровыми, представляя изображение в виде прямоугольной матрицы (сетки, целочисленной решетки) пикселей (растра), и большинство графических библиотек содержат внутри себя достаточное количество простейших растровых алгоритмов. На рис 2.1 приведена система растровых алгоритмов. n Алгоритмы растеризации n Алгоритмы перевода графических примитивов в растровую форму n Алгоритмы заполнения областей и многоугольников n Алгоритмы обработки растровых изображений n Регулировка яркости и контрастности n Масштабирование изображений n Геометрические преобразования n Алгоритмы фильтрации Алгоритмы растеризации Прежде чем перейдем к непосредственному рассмотрению возможности перевода математического описания объекта (линии и пр.) в растровую форму, рассмотрим понятие связности. Связность – возможность соединения двух пикселей растровой линией, т. е. последовательным набором пикселей. Возникает вопрос, когда пиксели (x1, y1) и (x2, y2) можно считать соседними. Для этого вводятся два понятия связности:
1. Четырехсвязность: пиксели считаются соседними, если либо их x-координаты, либо их y – координаты отличаются на единицу: |x1 – x2| + |y1 – y2| ≤ 1;
2. Восьмисвязность: пиксели считаются соседними, если их x-координаты и y-координаты отличаются не более чем на единицу: |x1 – x2| ≤ 1, |y1 – y2| ≤ 1.
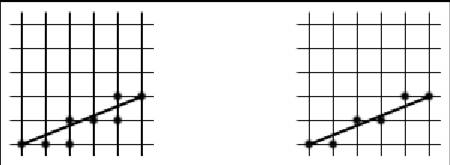
На рис. 2.2 изображены четырехсвязная и восьмисвязная линии.
Рис. 2.2. Четырехсвязная и восьмисвязная линии При переводе объектов в растровое представление существуют, алгоритмы, как использующие четырехсвязность, так использующие восьмисвязность. Растровая развёртка окружности Существует несколько очень простых, но не эффективных способов преобразования окружностей в растровую форму. Например, рассмотрим для простоты окружность с центром в начале координат. Ее уравнение записывается как x2 + y2 = R2. Решая это уравнение относительно y, получим y = ± Чтобы изобразить четвертую часть окружности, будем изменять x с единичным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычислений x и y по формулам x = R cos α, y = R sin α при пошаговом изменении угла α от 0° до 90°. Для упрощения алгоритма растровой развёртки стандартной окружности можно воспользоваться её симметрией относительно координатных осей и прямых y = ± x; в случае, когда центр окружности не совпадает с началом координат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем самым достаточно построить растровое представление для 1/8 части окружности, а все оставшиеся точки получить симметрией (см. рис. 2.5).
Рис. 2.5. Восьмисторонняя симметрия Рассмотрим участок окружности из второго октанта x Є [0, R/]. Далее опишем алгоритм Брезенхейма для этого участка окружности. На каждом шаге алгоритм выбирает точку Pi (xi, yi), которая является ближайшей к истинной окружности. Идея алгоритма заключается в выборе ближайшей точки при помощи управляющих переменных, значения которых можно вычислить в пошаговом режиме с использованием небольшого числа сложений, вычитаний и сдвигов. Рассмотрим небольшой участок сетки пикселов, а также возможные способы (от A до E) прохождения истинной окружности через сетку (рис. 2.6). Предположим, что точка Pi-1 была выбрана как ближайшая к окружности при x = xi-1. Теперь найдем, какая из точек (Si или Ti) расположена ближе к окружности при x = xi-1 + 1.
Рис. 2.6. Варианты прохождения окружности через растровую сетку
Заметим, что ошибка при выборе точки Pi (xi, yi) была равна D(Pi) = (xi2+ yi2) – R2. Запишем выражение для ошибок, получаемых при выборе точки Si или Ti: D(Si) = [(xi-1+ 1)2 + (yi-1)2] – R2; D(Ti) = [(xi-1+ 1)2 + (yi-1 – 1)2] – R2. Если | D(Si) | ≥ | D(Ti) |, то Ti ближе к реальной окружности, иначе выбирается Si. Введем di = | D(Si) | – | D(Ti) |. Ti будет выбираться при di ≥ 0, в противном случае будет устанавливаться Si. Опуская алгебраические преобразования, запишем di и di+1 для разных вариантов выбора точки Si или Ti. D1 = 3 – 2 R. Если выбирается Si (когда di < 0), то di+1 = di + 4 xi-1 + 6. Если выбирается Ti (когда di ≥ 0), то di+1 = di + 4 (xi-1 – yi-1) + 10. Существует модификация алгоритма Брезенхейма для эллипса.
procedure circle(x0,y0,r:integer); var d,d1,d2,x,y : integer; begin d:=0; y:=r; for x:=0 to round(r*sqrt(2.0)/2) do begin d1:=d+x+x+1; d2:=d1-y-y+1; if abs(d1) < abs(d2) then begin d:=d1; end else begin d:=d2; dec(y); end; put(x0+x,y0+y);put(x0+y,y0+x);put(x0-x,y0+y);put(x0+y,y0-x); put(x0+x,y0-y);put(x0-y,y0+x);put(x0-x,y0-y);put(x0-y,y0-x); end; end;
14. Алгоритм заполнения ограниченной области. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
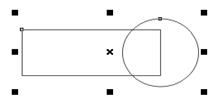 исходный объект
исходный объект объект после команды Сварить
объект после команды Сварить объект после команды Обрезать
объект после команды Обрезать объект после команды Пересечение
объект после команды Пересечение


 .
.
