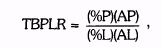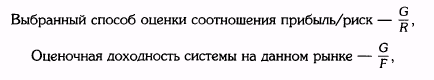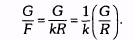ИЗМЕРЕНИЕ РЕЗУЛЬТАТИВНОСТИ, ОСНОВАННОЕ НА СДЕЛКАХ

В дополнение к только что описанным способам измерения результа­тивности, заслуживают определенного внимания следующие методы:

1. Ожидаемая чистая прибыль от сделки. Ожидаемая чистая прибыль от сделки (ENPPT) может быть выражена следующим образом:

ENPPT = (%Р)(АР) - (%L)(AL) ,

где %Р — процентная доля прибыльных сделок,

%L — процентная доля сделок, принесших чистые убытки,

АР — средняя чистая прибыль прибыльных сделок, AL — средний чистый убыток убыточных сделок.

Полезность этого индикатора состоит в том, что низкое значе­ние ENPPT будет указывать на системы, склонные к серьезному снижению эффективности при увеличении транзакционных зат­рат (из-за больших комиссионных, проскальзывания и т.д.). На­пример, если система имеет ENPPT в $50, обоснованность ее использования была бы в высшей степени подозрительна, неза­висимо от того, насколько хороши результаты других измерений ее производительности. Основной недостаток ENPPT состоит в том, что в ней отсутствует измерение риска. В дополнение

ГЛАВА 21. измерение результативности торговли 749

ENPPT содержит внутреннюю ловушку, состоящую в том, что она может показывать в необоснованно невыгодном свете актив­ные системы. Например, система, генерирующая одну сделку с чистым доходом в $2000, оценивалась бы лучше, чем система, которая в течение того же самого периода генерировала бы 100 сделок с ENPPT в $1000 (при сходных колебаниях активов).

2. Отношение прибыль/убытки, основанное на сделках.

КАКОЙ СПОСОБ

ИЗМЕРЕНИЯ РЕЗУЛЬТАТИВНОСТИ

СЛЕДУЕТ ИСПОЛЬЗОВАТЬ?

Рисковый компонент в RRR (AMR) ближе к интуитивному пониманию риска большинством людей, чем стандартное отклонение в коэффи­циенте Шарпа, которое не делает различий между внезапными больши­ми доходами и внезапными резкими убытками — двумя событиями, которые воспринимаются трейдерами (и инвесторами) очень по-разно­му. RRR, напротив, использует при измерении риска значение наихуд­шего для данного момента времени снижения стоимости активов. RRR, кроме того, избегает неспособности коэффициента Шарпа различать чередующиеся и последовательные убытки. По этим причинам RRR, вероятно, лучший показатель соотношения прибыльности и рискован­ности, чем коэффициент Шарпа.

Несмотря на это, RRR следует предложить, скорее, как дополнение, а не как замену. Причина: коэффициент Шарпа — очень широко ис­пользуемая мера отношения прибыльности и рискованности, в то вре­мя как на момент написания данной книги RRR вообще не использо­вался. Следовательно, трейдеру или разработчику системы все ещё нуж­но вычислять коэффициент Шарпа с целью сравнения собственных результатов с историей результативности других управляющих, промыш­ленных индексов или альтернативных инвестиций. Вместе коэффици­ент Шарпа и RRR предоставляют очень хорошее описание относитель­ной результативности системы или трейдера.

В дополнение к этим мерам соотношения прибыльности и риско­ванности следовало бы вычислять ENPPT, чтобы убедиться, что систе­ма устойчива к небольшому увеличению транзакционных затрат или небольшому снижению средней прибыльности сделок. Следует прове­рить размер максимального убытка (MR), чтобы убедиться в отсутствии катастрофических убытков. И наконец, можно вычислить AGPR в ка­честве дополнительной меры, дающей интуитивно понятное значение.

ГЛАВА 21. измерение результативности торговли 751

НЕАДЕКВАТНОСТЬ ОТНОШЕНИЯ ПРИБЫЛЬ/РИСК ОЛЯ ОЦЕНКИ ТОРГОВОЙ РЕЗУЛЬТАТИВНОСТИ ФИНАНСОВОГО УПРАВЛЯЮЩЕГО

В случае оценки торговых систем любой способ оценки соотношения прибыль/риск приводил бы к тому же порядку ранжирования систем, что и оценочная процентная доходность. Это наблюдение является следствием того факта, что величина требуемых для торговли с помо­щью системы средств может быть оценена лишь исходя из допустимого риска. Докажем его следующим образом:

где G — средний годовой доход на контракт,

R — выбранная мера риска (например, sd, AMR, ML),

F — общие активы, выделенные для торговли.

Единственный практический способ оценить F — рассматривать ее как функцию риска. Наиболее прямо F может оцениваться как выбран­ная мера риска, умноженная на некий коэффициент. То есть

F = kR,

где k — множитель меры риска (определяемый субъективно).

Таким образом, оценочный процент прибыли системы мог бы быть выражен как

Обратите внимание на то, что G/R — выбранная мера отношения при­были к риску. Следовательно, процентная доходность системы будет просто равна мере отношения прибыль/риск, умноженной на некото­рую константу. Хотя разные трейдеры будут выбирать различные меры риска и значения k, как только эти величины определены, мера отно­шения прибыли к риску и доходность будут приводить к оценке систем, располагающей их в одном и том же порядке. Кроме того, заметьте, что

752 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

в случае оценки торговых систем значение процентного риска, кото­рое мы определяем как меру риска, деленную на требуемые активы, неизменно (процентный риск = R/F = R/kR = 1/k).

В то время как в случае оценки торговых систем более высокий коэффициент прибыль/риск всегда подразумевает более высокий про­цент прибыли, это неверно в случае оценки финансовых управляющих. Кроме того, процентный риск более не является константой, но вмес­то этого может меняться от управляющего к управляющему. Таким об­разом, вполне возможно, что у финансового управляющего более вы­сокий коэффициент прибыль/риск, чем у другого, но при этом у него ниже доходность или выше процентный риск. (Причина в том, что в случае финансового управляющего связь между требуемыми активами и риском нарушена, т.е. различные финансовые управляющие будут различаться уровнем риска, который они допускают для данного уров­ня активов.) Следовательно, отношение прибыльности к рискованнос­ти более не является достаточной мерой результативности при выборе между альтернативными инвестициями. Мы иллюстрируем этот момент, используя коэффициент Шарпа, но похожие выводы применимы и к другим мерам прибыль/риск. (В последующем обсуждении мы предпо­лагаем, что оплата управляющего полностью основана на прибыли и что доход от процентов по безрисковой ставке не включается в прибыль финансового управляющего, но получается инвесторами. Следователь­но, годится упрошенная форма коэффициента Шарпа, которая не учи­тывает безрисковые процентные ставки.)

Предположим, что у нас есть следующая годичная статистика, ка­сающаяся двух финансовых управляющих:

Хотя коэффициент Шарпа у менеджера В выше, не все трейдеры пред­почли бы менеджера В, поскольку его мера риска выше (более высо­кое стандартное отклонение). Таким образом, не склонный к риску ин­вестор мог бы предпочесть менеджера А, будучи готовым пожертвовать возможностью получения более высокой прибыли ради того, чтобы из­бежать существенно более высокого риска. Например, если годовые результаты торговли нормально распределены для любого данного года, было бы 10% вероятности падения прибыли более чем на 1,3 стандар­тного отклонения ниже ожидаемого уровня. При таком повороте

ГЛАВА 21. измерение результативности торговли 753

событий инвестор потерял бы $54 000, работая с менеджером В ($50 000 — (1,3 х $80 000)], но лишь $16 000, работая с менедже­ром А. Для не склонного к риску инвестора минимизация убытков в рамках негативных предположений может оказаться важнее, чем мак­симизация дохода при благоприятных обстоятельствах*.

Рассмотрим теперь статистику двух других финансовых управляющих:

Менеджер С Менеджер D

Хотя у менеджера D более высокий коэффициент Шарпа, менеджер С показывает существенно более высокую доходность. Умеренно консер­вативные инвесторы могли бы предпочесть менеджера С даже несмот­ря на то, что его коэффициент Шарпа ниже. Причина состоит в том, что в значительной части вероятных исходов инвестор получил бы луч­ший результат у менеджера С. В этом конкретном примере результат был бы лучше до тех пор, пока прибыль не падает более чем на 0,93 стандартной отклонения ниже ожидаемого уровня — условие, которое выполнялось бы в 82% случаев (предполагая, что результаты торговли нормально распределены)**.

* Подразумеваемые предположения в этом примере: инвестор не может раз-

местить часть установленных начальных инвестиций у менеджера В. Другими словами, минимальный размер единицы инвестиций равен $100 000. Иначе было бы всегда возможно разработать стратегию, при которой инвестору вы­годнее работать с менеджером, имеющим более высокий коэффициент Шар­па. Например, размещение $25 000 у менеджера В подразумевало бы то же самое стандартное отклонение, что и случай инвестирования $100 000 через менеджера А, но при более высокой ожидаемой прибыли ($12 500).

** Подразумеваемое предположение этого примера: цена заимствований для

инвестора существенно выше, чем безрисковый процентный доход, фиксиру­емый при размещении средств у финансового управляющего. Это предполо­жение исключает возможность альтернативной стратегии, состоящей в заим­ствовании средств и размещении заимствованной суммы (в несколько раз боль­шей, чем начальные инвестиции размером в $100 000) у менеджера с более высоким коэффициентом Шарпа. Если бы цена заимствований и безрисковый процентный доход были равны (чего в реальной жизни, как правило, не бы­вает), всегда можно было бы разработать стратегию, при которой инвестор получал бы лучший результат с тем менеджером, у которого более высокий коэффициент Шарпа. Например, стратегия заимствования дополнительных $400 000 и размещения $500 000 у менеджера D подразумевала бы то же самое стандартное отклонение, что и случай инвестирования $100 000 через менеджера С, но при более высокой ожидаемой прибыли ($25 000).

754 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

Еще более поразителен тот факт, что существуют обстоятельства, при которых фактически все инвесторы предпочли бы финансового управляющего с более низким коэффициентом Шарпа. Рассмотрим сле­дующих двух управляющих*:

В этом примере фактически все инвесторы (даже не склонные к риску) предпочли бы менеджера F, несмотря на то, что его коэффициент Шар­па ниже. Причина в том, что доходность в данном случае настолько велика по сравнению со стандартным отклонением, что даже при чрез­вычайно неблагоприятных обстоятельствах инвесторы почти гаранти­рованно получили бы лучший результат у менеджера F. К примеру, если результаты торговли нормально распределены, то вероятность получе­ния прибыли более чем на 3 стандартных отклонения ниже ожидаемой прибыли составляет только 0,139%. Даже при этих экстремальных об­стоятельствах инвестор получил бы лучшие результаты у менеджера F: прибыль = $12500/год (12,5%) по сравнению с $4000/год (4%) у ме­неджера Е. Этот пример показывает еще нагляднее, что само по себе отношение прибыльности к рискованности не дает достаточно инфор­мации для оценки финансового управляющего**.

(Этот вывод применим ко всем способам измерения соотношения прибыли и риска, а не только к коэффициенту Шарпа.)

Наиважнейший вывод состоит в том, что при оценке финансовых управляющих важно рассматривать доходность и риск как независимые величины, а не просто их отношение.

* Значения коэффициента Шарпа, использованные в этом примере, замет-

но выше, чем те уровни, с которыми можно столкнуться в действительности.
Мы предполагаем столь высокие значения для иллюстрации теоретического
момента.
** Здесь применимы те же комментарии, что и в сноске на стр. 699.

ГЛАВА 21.измерение результативности торговли 755

Не нашли, что искали? Воспользуйтесь поиском по сайту: