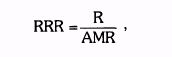ОТНОШЕНИЕ ПРИБЫЛИ К МАКСИМАЛЬНОМУ ПАДЕНИЮ СТОИМОСТИ АКТИВОВ (RETURN RETRACEMENT RATIO — RRR)

RRR предлагает меру соотношения доходности и риска, которая позво­ляет избежать недостатков коэффициента Шарпа, обсуждавшихся в предыдущем разделе. Кроме того, RRR ближе к восприятию риска боль­шинством трейдеров. RRR представляет собой среднюю прибыль с уче­том реинвестирования (R), пересчитанную в годовом исчислении и де­ленную на усредненное за год максимальное снижение стоимости ак­тивов (average maximum retracement measure — AMR):

ГЛАВА 21. измерение результативности торговли 743

R можно вычислить как отношение суммарного прироста стоимос­ти активов управляющего или системы за год, к величине активов на начало года, при условии, что полученная прибыль оставалась на тор­говом счету. Очевидно, что при расчете R будут учтены все реинвести­ции прибыли, совершенные управляющим. AMR равен усредненному за год максимальному месячному снижению стоимости активов (MR), где MR равна большей из следующих двух величин:

1. Максимальному снижению с момента предыдущего пика стоимо­-
сти активов (MRPP),

2. Максимальному снижению до последующего минимума стоимо­-
сти активов (MRSL).

Как подразумевает название, MRPP измеряет, на сколько процентов снизились активы по сравнению с наивысшей их предыдущей точкой. В результате для данных в каждой точке (например, в конце месяца) MRPP отражает наихудшую переоценку, с которой теоретически мог бы столкнуться любой инвестор, работающий со счетом в этот момент. MRPP равна совокупным потерям, которые были бы зафиксированы инвестором, начинающим торговать в наихудший возможный предше­ствующий момент времени (в момент наивысшей стоимости активов). Заметьте, что, если новый пик активов установлен в данном месяце, MRPP для этой точки будет равна нулю. Одна из проблем, связанных с MRPP, состоит в том, что для начальных точек всего объема данных эта мера падения стоимости активов может быть недооценена, поскольку существует лишь малое количество предыдущих точек.

Как подразумевает название, MRSL измеряет процентное снижение активов до последующей самой низкой точки. В результате для данных в каждой точке (например, на конец месяца) MRSL измеряет наихуд­шую переоценку, с которой в любой момент могли бы столкнуться ин­весторы, начинающие торговать в этом месяце, т.е. совокупные поте­ри, которые были бы зафиксированы подобными инвесторами в сле­дующей точке минимальной стоимости активов. Заметьте, что если сто­имость активов никогда не снижалась ниже уровня данного месяца, MRSL для этой точки будет равна нулю. Одна из проблем, связанных с MRSL, состоит в том, что для последних точек всего объема данных эта мера падения стоимости активов, скорее всего, будет недооценена, поскольку в последующих данных (при их наличии) мог бы содержать­ся новый минимум стоимости активов.

MRPP и MRSL дополняют друг друга. Заметьте, что их одновремен­ная недооценка маловероятна. По этой причине, MR для каждой точ­ки определяется как набольшая величина из MRPP и MRSL. В этом смысле MR представляет действительно наихудший сценарий для каж­дой точки (например, для конца месяца). AMR усредняет наихудшие

744 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

возможные сценарии. Этот подход значительно более основателен, чем методы, использующие лишь единственный наихудший случай — мак­симальное снижение стоимости активов.

Математическое определение RRR дано ниже:

где R — средняя годовая прибыль с учетом реинвестиций

(вывод смотри ниже);

где E_i — стоимость активов на конец месяца i,

РЕ_i — пик стоимости активов в месяц i или до него, Е_i-1 — стоимость активов на конец месяца,

предшествующего месяцу i, ME_i — минимум стоимости активов в месяц i или в следующий за ним месяц.

Заметьте, что MRPP, будет равной нулю для первого месяца, а MRSL, будет равна нулю для последнего месяца.

Средняя годовая прибыль с учетом реинвестиции R выводится сле­дующим образом*:

* Следующий в примере вывод R, где R = 0,30, взят из статьи Дж. Швагера «Alternative to Sharpe Ratio Better Measure of Performance», Futures, p. 58, March 1985.

ГЛАВА 21. измерение результативности торговли 745

В(1 + R)^N = Е ,

где S — стартовая стоимость активов,

Е — конечная стоимость активов,

N — количество лет,

R — доходность в процентах годовых с учетом реинвестирования (в десятичной форме).

Отсюда формула для доходности в процентах годовых (R):

Чтобы облегчить решение этого уравнения относительно R, можно выразить его в терминах десятичных логарифмов:

Например, если счет в $100 000 вырос до $285 610 за четыре года, доходность в процентах годовых с учетом реинвестирования была бы равна 30%*:

* Пример рабочего листа Excel для вычисления RRR предложен в книге «Schwager on Futures: Managed Trading».

746 ЧАСТЬ 4. торговые системы и измерение эффективности торговли

Хотя это и не влияет на вычисления, для выбора правдоподобной величины трейдер может предположить, что активы, необходимые для торговли с помощью системы, в четыре раза превышают максимальные убытки. Например, если максимальный убыток системы составляет $50 000, для торговли с помощью этой системы предположительно не­обходимы активы, равные $200 000.

Как только размер активов, необходимых для торговли с помощью системы (т.е. предполагаемый размер счета), выбран, месячные разме­ры активов могут быть получены следующим образом:

1. Поделите все месячные значения прибылей/убытков на один и
тот же размер счета, чтобы получить месячные значения про­-
центной прибыли**.

2. Используйте цепь умножений подразумеваемого размера счета
на значения месячной процентной прибыли, чтобы получить ме­-
сячные уровни активов. Например, если предполагаемый раз­-
мер счета $200 000, а процентные прибыли за первые четыре
месяца составили +4, -2, -3 и +6%, тогда соответствующие
уровни активов вычислялись бы следующим образом:

Начало = $200 000.

Конец месяца 1 = (200 000) (1,04) = $208 000.

Конец месяца 2 = (200 000) (1,04) (0,98) = $203 840.

Конец месяца 3 = (200 000) (1,04) (0,98) (0,97) = $197 725.

Конец месяца 4 = (200 000) (1,04) (0,98) (0,97) (1,06) = $209 588.

Когда получены месячные уровни активов, вывод значений R и AMR для вычисления RRR будет в точности аналогичен случаю оценки фи­нансового управляющего.

Следует заметить, что в реальной торговле каждый корректировал бы используемые для торговли активы, основываясь на личных взгля-

* Поскольку предполагаемый размер активов используется как делитель и в числителе, и в знаменателе RRR, он будет сокращен. Например, удвоение раз­мера предполагаемого счета сокращало бы наполовину как среднюю годовую прибыль с учетом реинвестиций, так и усредненное за год максимальное сни­жение стоимости активов, оставляя значение RRR неизменным.

** Обратите внимание на то, что торговые результаты системы основывают-

ся на фиксированном портфеле. Другими словами, при тестировании систе­мы количество контрактов не увеличивается, когда система зарабатывает день­ги, и не уменьшается, когда система терпит убытки. (В действительной торгов­ле, конечно, такие поправки были бы сделаны.) Таким образом, использова­ние постоянного размера счета в качестве делителя при переводе отношения прибыль/убытки в процент прибыли является допустимой процедурой.

ГЛАВА 21. измерение результативности торговли 747

дах на риск. Действительный используемый уровень мог бы быть боль­ше или меньше, чем четырехкратный размер максимальных потерь, ко­торый мы использовали как начальное предположение при вычислении RRR для системы. Однако на значении RRR системы никак не сказы­вался бы определенный выбор размера счета, рассматриваемого как необходимый для торговли с помощью системы.

Не нашли, что искали? Воспользуйтесь поиском по сайту: