
|
|
Понятие о лобовом сопротивлении в выработках. Особенности расчета сопротивления шахтных стволов.Лобовое сопротивление имеет место при обтекании воздухом неподвижного тела или при движении тела в неподвижной среде. Потеря напора, вызванная лобовым сопротивлением, определяется по формуле:
где с- сечение выработки в свету, м2; S - миделево сечение (проекция тела на плоскость, нормальную к оси потока).
Миделево сечение крепи штрекообразных выработок равно проекции крепи на плоскость, нормальную к оси выработки. Обычно у стенки выработки скорость воздуха минимальна, поэтому данный вид сопротивления не играет существенной роли в общем сопротивлении выработки и учитывается общим аэродинамическим коэффициентом a(см. уравнение 11.9). Наибольшее значение коэффициента лобового сопротивления в шахтных условиях имеют расстрелы в вертикальных стволах. При большой глубине стволов потеря депрессии в них, вызванная большим лобовым сопротивлением их армировки, может в несколько раз превышать депрессию остальной части горных выработок шахты. Применение расстрелов и обтекателей аэродинамически совершенной формы (гексагональной, овальной, каплевидной) позволяет уменьшить величину депрессии стволов в 2÷2,5 раза. 14.Местные сопротивления и их расчет. Привести рисунок и дать пояснение. Местными сопротивлениями являются различного рода препятствия на пути движения воздуха. К ним относятся: повороты и сопряжения выработок, кроссинги, двери с окнами, внезапные сужения и расширения струи, движущиеся поезда и другие загромождения выработок. Местные сопротивления вызывают потерю живой силы потока. Величина потери потока напора, вызванная местными сопротивлениями, определяется по формуле:
где путем и приводится в справочниках для наиболее распростра- ненных видов местных сопротивлений; u- средняя скорость движения воздуха до или после местного со- противления, м/сек. Общая потеря давления воздуха в выработке равна сумме потерь, затрачиваемых, соответственно, на преодоление трения (hтр) и местных сопротивлений (hм):
15. Понятие о законах аэростатики и ее основные задачи. Формула для расчета аэростатического давления.Аэростатика – наука о равновесии газов (воздуха). Она исследует условия, при которых воздух может находиться в неподвижном состоянии – состоянии равновесия. Одной из основных задач аэростатики является определение изменения давления с высотой (глубиной) в покоящемся воздухе, а также условий равновесия находящегося в воздушной среде тела. Давление, с которым имеют дело в аэростатике, называется аэростатическим; оно вызывается весом вышележащих слоев воздуха. Основное уравнение аэростатики в проекциях на координатные оси имеет вид: dp = r·(X·dx + Y·dy + Z·dz), (10.6) где р- давление; r - плотность воздуха; X, Y, Z – проекции объемной силы, отнесенной к единице массы; x, y, z - координаты. Под объемной (или массовой) силой понимается сила, действующая на каждую частицу воздуха во всем его объеме (например, силы тяжести и инерции). При неподвижной атмосфере в шахте единственной объемной силой является сила тяжести. Если ось Оzнаправить вертикально вниз, получим Z=g и основное уравнение аэростатики будет: dp=r·g·dz, (10.7) где g - ускорение силы тяжести. Если начало координат расположить на поверхности земли (в устье ствола), то давление на глубине h=z определится интегрированием 10.7 при граничном условии z=0, p=p0:
Если в какой-либо выработке r=const или при переменной плотности ее можно характеризовать некоторой средней величиной, то из уравнения 10.8 получим: p=p0+g·r·h, (10.9) где h - разность отметок начала и конца выработки.
Уравнение 10.7 можно переписать в виде: dp=g ·dz, (10.10) где g -удельный вес воздуха. Его изменение с глубиной зависит от изменения состояния воздуха, которое приближенно можно описать одним из следующих процессов: изохорическим –g=const; изотермическим – Т= соnst; адиабатическим – dQ= const или Здесь Т – абсолютная температура воздуха; Q –количество содержащегося в воздухе тепла; n- показатель политропы (1<n<1,41). Используя эти зависимости, а также уравнение состояния газа
гдеR – газовая постоянная. После интегрирования выражения (10.10) в пределах от z=0 до h при граничных условия z=0, p=p0, T=T0, g=g0, получим следующие законы изменения давления с глубиной: изохорический процесс p=p0+g0·h; (10.12) изотермический процесс
адиабатический и политропический процессы
где k=1.41 – для адиабаты и k= n – для политропы. Формулы для изотермического, адиабатического и политропического процессов дают весьма близкие результаты. Поскольку формула (10.13) наиболее проста, целесообразно использовать ее для определения приращения давления с глубиной. Следует иметь в виду, что при расчетах по формулам (10.12) и (10.14) начальное давление p0 должно иметь размерность в той же системе, что и остальные величины; при расчете по формуле (10.13) это не обязательно и р0можно выразить в мм. рт.ст., атмосферах и т.д. Формулы (10.12) - (10.14) носят название барометрических формул. Из них, в частности, следует, что приращение давления не зависит от поперечных размеров столба воздуха, т.е. давление в выработке не зависит от площади ее поперечного сечения и, следовательно, от его изменения по длине. Весьма важным свойством воздушной среды является то, что давление, действующее в данной ее точке, одинаково во всех направлениях и что изменение давления в какой– либо точке, не вызывающее заметных эффектов сжатия, вызывает такое же изменение давления во всех остальных точках среды. Данное свойство носит название закона Паскаля. Согласно ему, уменьшение давления на поверхности, например, на 5 мм.рт.ст., вызовет уменьшение давления во всех выработках шахты также на 5 мм.рт.ст. Из закона Паскаля следует, что давление, воспринимаемое пластинкой, расположенной в данной точке пространства, не зависит от ее ориентации в пространстве. Следовательно, давления на одну и на другую ее плоскость равны. Поскольку давление действует по нормали к поверхности, то равнодействующая сил давления, приложенных к пластинке, равна нулю, т.е. аэростатическое давление не может вызвать перемещения тела. Из закона Паскаля следует, что давление на все стенки выработки, расположенные на одной вертикальной высоте, в неподвижном воздухе одинаково. Согласно закону Архимеда, на находящееся в воздухе тело действует выталкивающая сила Р, направленная вертикально вверх и численно равная весу воздуха в объеме тела: Р=V·g, (10.15) где V- объем тела; g- средний удельный вес воздуха на уровне расположения тела. Следовательно, при весе тела V·g< P оно всплывает, при V·g =P тело находится в равновесии и при V·g> P тело опускается. Атмосферное давление в шахте неоднозначно: в более глубоких выработках оно больше, чем в менее глубоких [см. формулы (10.12-10.14)]. Изменение атмосферного давления на поверхности вызывает такое же по величине и знаку изменение давления воздуха в шахте. Работа вентилятора изменяет атмосферное давление в шахте: при всасывающей вентиляции оно меньше, при нагнетательной – больше давления в неподвижном воздухе. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 кг/м2 , (11.12)
кг/м2 , (11.12)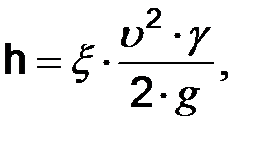 кг/м2 ,(11.10)
кг/м2 ,(11.10) - коэффициент местного сопротивления, определяется опытным
- коэффициент местного сопротивления, определяется опытным кг/м2.
кг/м2.  (10.8)
(10.8)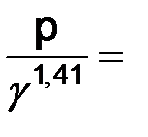 const; политропическим –
const; политропическим –  соnst.
соnst. , (10.11)
, (10.11)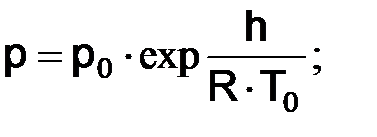 (10.13)
(10.13) , (10.14)
, (10.14) ;
;