
|
|
Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.Для иллюстрации закона Паскаля на рис. 1.15.1 изображена небольшая прямоугольная призма, погруженная в жидкость. Если предположить, что плотность материала призмы равна плотности жидкости, то призма должна находиться в жидкости в состоянии безразличного равновесия. Это означает, что силы давления, действующие на грани призмы, должны быть уравновешены. Это произойдет только в том случае, если давления, т. е. силы, действующие на единицу площади поверхности каждой грани, одинаковы: p1 = p2 = p3 = p.
Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости. Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg, где m = ρghS – масса жидкости в сосуде, ρ – плотность жидкости. Следовательно
Такое же давление на глубине h в соответствии с законом Паскаля жидкость оказывает и на боковые стенки сосуда. Давление столба жидкости ρgh называют гидростатическим давлением. Если жидкость находится в цилиндре под поршнем (рис. 1.15.2), то действуя на поршень некоторой внешней силой Таким образом, полное давление в жидкости на глубине h можно записать в виде:
Если на рис. 1.15.2 поршень убрать, то давление на поверхность жидкости будет равно атмосферному давлению: p0 = pатм.
Закон сохранения массы в движущемся воздухе. Привести уравнение неразрывности и соотношение между скоростью и сечением выработки. Закон сохранения массы — закон физики, согласно которому масса физической системы сохраняется при всех природных и искусственных процессах. В исторической, метафизической форме, согласно которой вещество несотворимо и неуничтожимо, закон известен с древнейших времён. Позднее появилась количественная формулировка, согласно которой мерой количества вещества является вес (позднее — масса). С точки зрения классической механики и химии, сохраняются общая масса закрытой физической системы, равная сумме масс компонентов этой системы (то есть масса считается аддитивной). Этот закон с большой точностью верен в области применимости ньютоновской механики и химии, так как релятивистские поправки в этих случаях пренебрежимо малы. Уравнения неразрывности В основе уравнения неразрывности находится закон сохранения массы. Оно характеризует также непрерывность распределения (сплошность) массы, т.е. отсутствие пустот в жидком теле.
- уравнение неразрывности (сплошности) в дифференциальной форме. Если движение жидкости установившееся, то
Для несжимаемой жидкости ( =const) при установившемся движении имеем:
Для установившегося течения несжимаемой жидкости элементарной струйки тока закон сохранения массы означает, что расход во всех сечениях элементарной струйки один и тот же, т.е.
Аналогичное соотношение можно составить для потока конечных размеров, введя в рассмотрение вместо скоростей и струек среднюю скорость потока V; таким образом, по длине потока
т.е. величины средней скорости в сечениях потока несжимаемой жидкости обратно пропорциональны площадям соответствующих сечений. 7. Диагональное соединение выработок. Их депрессия и сопротивление. Привести рисунок и дать пояснение. Основная особенность диагонали Простое диагональное соединение выработок. Общая депрессия диагонального соединения (между точками АиD , рис. 13.2) определяется по формулам:
Общее аэродинамическое сопротивление (между точками АиD):
где
Рисунок 13.2– Схема простого диагонального соединения При известном RADобщая депрессия диагонального соединения: hAD = RAD × Q2.(13.14) Направление движения воздуха в диагонали ВСпроисходит от Вк С при R2 /R1> R5/R4и от СкВ при R2 /R1< R5/R4.При R2 /R1=R5/R4 движение отсутствует. В первых двух случаях распределение воздуха по ветвям простого диагонального соединения определяется графоаналитически, способом последовательных приближений или с помощью какого-либо вычислительного устройства; в третьем случае– по формулам параллельного соединения, получающегося при изъятии диагонали ВС. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|


 можно создавать в жидкости дополнительное давление p0 = F / S, где S – площадь поршня.
можно создавать в жидкости дополнительное давление p0 = F / S, где S – площадь поршня.
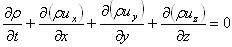
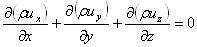
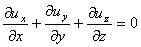
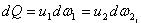
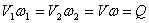
 ; (13.11)
; (13.11) . (13.12)
. (13.12) , (13.13)
, (13.13) ;
;  .
.