
|
|
Двойственная задача и теорема двойственностиОпределение 9.Следующая задача называется двойственной к задаче (1,2). Задача 3. Найти
где матрицы A, b,c определяются по формулам (3), а В развернутой форме эта стандартная задача линейного программирования может быть записана в следующем виде. Задача 3’. Найти минимум линейной функции
при ограничениях:
Задачи (1, 2) и (91, 92) называются взаимно двойственными задачами, а задача (1, 2) по отношению к задаче (91, 92) называется прямой. Пример 9. Составить двойственные задачи к следующим задачам.
Решение. a) Число переменных в двойственной задаче совпадает с числом ограничений прямой задачи и равно 3. Обозначим их через
b)Прежде чем составить двойственную задачу следует прямую задачу преобразовать так, чтобы все неравенства в ней имели вид «
Для решения двойственной задачи можно применить те же методы решения, как и для прямой задачи: составление канонической задачи, поиск допустимого базисного плана, преобразование таблиц. Однако, всего этого можно избежать, если есть базисное решение прямой задачи. Базисное решение двойственной задачи можно взять из строки для целевой функции прямой задачи. А для проверки оптимальности полученного решения можно воспользоваться теоремой двойственности. Теорема двойственности. Пусть и допустимые решения задач и соответственно, тогда 1. 2. Если Рассмотрим следующий пример решения двойственной задачи и проверки его по теореме двойственности. Пример 10. Найти решение двойственной задачи к задаче примера 8 и проверить его по теореме двойственности. Решение. Двойственной задачей к задаче (15, 16) будет задача (21, 22). Итоговой таблицей прямой задачи будет таблица 11. Меняя знаки у чисел стоящей в последней строчке, мы укажем значения переменных двойственной задачи.
Проверим теперь допустимость полученного решения. Для этого подставим их в неравенства системы (22). Мы получим
Следовательно, план
Это значение совпадает с сосчитанным ранее значением целевой функции прямой задачи. А поэтому приведенный нами план двойственной задачи (23) будет оптимальным. Пример решения задачи Задача 4. Найти максимум линейной функции
В математических символах эта задача имеет следующий вид:
1. Запишем эту задачу в матричной форме. Для этого умножим первое и третье неравенство системы на –1. У нас получиться следующая система неравенств:
Следовательно, наша задача в матричной форме примет вид:
где
2.Для построения канонической задачи введем дополнительные переменные
Окончательно, каноническая задача линейного программирования для нашей задачи имеет вид:
 3. Для того чтобы решить начальную задачу геометрически, построим прямые 3. Для того чтобы решить начальную задачу геометрически, построим прямые  , , 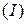 ; ;  , ,  ; ;  , ,  ,. ,.
 и будем ее передвигать в направлении вектора и будем ее передвигать в направлении вектора 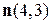 . Свое максимальное значение на множестве . Свое максимальное значение на множестве 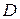 функция функция 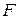 примет в точке примет в точке  . Найдем ее координаты. Для этого решим систему уравнений: . Найдем ее координаты. Для этого решим систему уравнений:  , ,  . .
Функция 4. Если за базисные переменные канонической задачи (25) взять переменные
Составим симплекс-таблицу и применим симплекс метод. В таблицы включена также функция
Из этой таблицы мы находим допустимый базисный план канонической задачи:
5. Исключим теперь из таблицы вспомогательную функцию
Из последней таблицы мы получим оптимальное решение канонической задачи (25):
а следовательно функция 6. Двойственная задача к искомой задаче будет иметь вид:
или в матричной форме: 7. Из последней симплекс таблицы мы найдем значения двойственных переменных:
Подставим эти числа в ограничения двойственной задачи и целевую функцию:
Так как выполнены все условия теоремы двойственности, то найденное решение:
будет оптимальным решением двойственной задачи.
Варианты заданий
Литература
Учебное издание
ЛУЦЕНКО МИХАИЛ МИХАЙЛОВИЧ
Отпечатано в авторской редакции
Подписано в печать с оригинал макета – 6.04.2006 Формат 60х80 1/16. Бумага для множ. апп. Печать офсетная. Усл.печ.л. Уч.-изд.л. Тираж Заказ Цена Петербургский государственный университет путей сообщения. 190031, СПб., Московский пр., 9. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 , (19)
, (19) ,
,  , (20)
, (20) .
.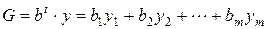 ,
, 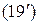

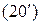
 .
. ,
,
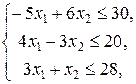
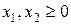 .
.
 ,
,

 Так как в прямой задаче требуется найти максимум, то знаки неравенств во всех ограничениях должны быть «
Так как в прямой задаче требуется найти максимум, то знаки неравенств во всех ограничениях должны быть « 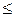 ». Коэффициенты целевой функции двойственной задачи совпадают со свободными частями неравенств, а правые части неравенств двойственной задачи совпадают с коэффициентами целевой функции прямой задачи. В итоге мы получаем следующую задачу линейного программирования.
». Коэффициенты целевой функции двойственной задачи совпадают со свободными частями неравенств, а правые части неравенств двойственной задачи совпадают с коэффициентами целевой функции прямой задачи. В итоге мы получаем следующую задачу линейного программирования. ,
,
 .
. ». Для этого мы умножим первые два неравенства на –1. После этого мы уже сможем записать двойственную задачу.
». Для этого мы умножим первые два неравенства на –1. После этого мы уже сможем записать двойственную задачу. , (21)
, (21)
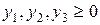 . (22)
. (22)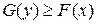 .
. , то
, то 
 – оптимальные решения соответствующих задач.
– оптимальные решения соответствующих задач.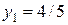 ,
,  ,
, 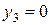 (23)
(23) ,
,  .
.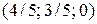 является допустимым для задачи (15, 16). Вычислим теперь значение целевой функции на этом плане. У нас получиться:
является допустимым для задачи (15, 16). Вычислим теперь значение целевой функции на этом плане. У нас получиться: .
.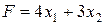 , если переменные
, если переменные  удовлетворяют следующей системе ограничений:
удовлетворяют следующей системе ограничений:
 ,
,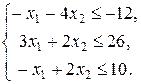
 ,
,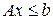 ,
,  ,
, ;
;  ;
;  ;
; 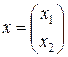 (24)
(24) и запишем систему ограничений задачи в виде
и запишем систему ограничений задачи в виде
 .
. при ограничениях
при ограничениях
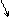





 и отметим стрелочками те полуплоскости, в которых выполняются соответствующие неравенства. Областью допустимых решений задачи оказался четырехугольник.
и отметим стрелочками те полуплоскости, в которых выполняются соответствующие неравенства. Областью допустимых решений задачи оказался четырехугольник.

 в точке с координатами
в точке с координатами  ;
;  .
. , то соответствующий базисный план будет недопустим. Для построения начального плана введем искусственную переменную
, то соответствующий базисный план будет недопустим. Для построения начального плана введем искусственную переменную  и составим вспомогательную задачу.
и составим вспомогательную задачу. ,
,
 .
. , а генеральные строки и столбцы таблиц заштрихованы.
, а генеральные строки и столбцы таблиц заштрихованы.


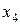




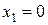 ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  ,
, 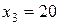 ,
,  ,
,  ,
,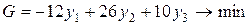 ,
,
 ,
, 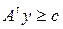 ,
,  с матрицами (24) и матрицей
с матрицами (24) и матрицей  .
. ,
, 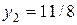 ,
, 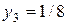
 ,
,  ,
,  .
. ,
,  ,
,

 ,
,
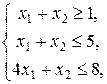
 ,
,

 ,
,

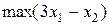 ,
,

 ,
,
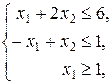


 ,
,

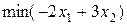 ,
,

 ,
,

 ,
,
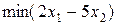 ,
,

 ,
,

 ,
,

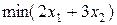 ,
,

 ,
,



 ,
,
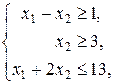

 ,
,
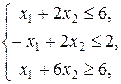


 ,
,
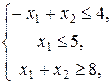
 ,
,

 ,
,

 ,
,

 ,
,

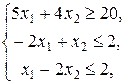

 ,
,
