
|
|
Составление новой симплекс таблицы.· Имена всех базисных переменных сохраняются за исключением имени генеральной строки. Оно заменяется именем переменной генерального столбца. · Элементы генеральной строки делятся на генеральный элемент, и полученные значения заносятся в новую таблицу. В частности, на месте генерального элемента записывается единица. · Остальные элементы генерального столбца заменяются нулями. · Для элемента
где Компактно это преобразование таблицы можно записать в виде формулы:
Пример 7. Решить следующую каноническую задачу линейного программирования симплекс-методом.
при ограничениях
Решение. В этой задаче легко выделить базисные и свободные переменные. Полагая значения свободных переменных Таблица 3. Таблица 4.
Эта таблица не порождает оптимальное базисное решение, так как в последней строке стоят два положительных числа. Возьмем одно из них, например 7. Следовательно, первый столбец будет генеральным. Найдем теперь отношения свободных членов к положительным элементам генерального столбца: Переменную Заполним клетку помеченную символом (·). Соответствующие элементы генеральной строки и столбца будут равны: Таблица 5. Таблица 6.
Таблица 5 порождает следующее базисное решение задачи:
Значение целевой функции будет Найденное нами базисное решение не оптимально, так как в последней строке Таблицы 5 есть положительные элементы. Для нахождения следующего базисного плана выберем базисный столбец симплекс-таблицы 5. Так как в последней строке положительный элемент только один, то за такой столбец следует взять столбец Как и ранее вычислим отношения свободных членов к положительным элементам генерального столбца. У нас получатся следующие отношения: Выполним преобразование таблицы 5 и составим таблицу 6. Составление этой таблицы удобно начинать с последней строки, так как именно по ней определяется оптимальность получаемого решения. Так как все элементы последней строки оказались отрицательными, то порождаемое этой таблицей базисное решение
будет оптимальным, а минимальное значение целевой функции Построение допустимого плана с помощью искусственного базиса Как мы уже отмечали, преобразования симплекс метода могут выполняться только с базисного допустимого решения. Однако поиск такого решения также довольно непрост. Формально мы должны перебирать базисные решения до тех пор пока мы не найдем неотрицательное или не покажем что таких не существует. В этом параграфе мы покажем, как симплекс-методом можно найти базисное допустимое решение или доказать, что система ограничений канонической задачи несовместна. Предположим, что в системе уравнений (12) значения свободных членов отрицательны. Умножим эти уравнения на –1 и составим новую систему уравнений:
В этой системе искусственные переменные Составим новую задачу:
Наименьшее возможное значение вспомогательной целевой функции Если же минимальное значение вспомогательной функции Пример 8. Решить следующую задачу линейного программирования симплекс методом.
при ограничениях
Решение. Введем дополнительные переменные
и перейдем к канонической задаче линейного программирования.
при ограничениях
Если в этой задаче переменные Введем искусственную переменную
и составим вспомогательную целевую функцию:
в записи которой базисная переменная
при ограничениях
Для этой задачи составим симплекс-таблицу 7. В эту таблицу мы включили первоначальную целевую функцию Таблица 7. Таблица 8.
За генеральный столбец в таблице 7 мы возьмем столбец Переменная
Заметим, что значение целевой функции Таблица 9. Таблица 10.
В этой таблице выберем генеральный элемент и выполним преобразование таблицы. У нас получиться Таблица 10. В этой таблице значение целевой функции Таблица 11.
Все элементы последней строки отрицательны. Следовательно эта таблица порождает оптимальное базисное решение задачи (17, 18). А именно,
При этом минимальное значение функции равно –36. Минимальное значение функции 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 исходной таблицы находятся соответствующий ему элемент генеральной строки
исходной таблицы находятся соответствующий ему элемент генеральной строки  и элемент
и элемент  генерального столбца. На месте этого элемента в новой таблице пишется
генерального столбца. На месте этого элемента в новой таблице пишется  , (13)
, (13) – генеральный элемент.
– генеральный элемент.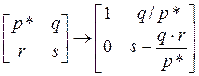
 ,
,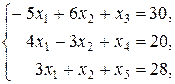
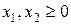
 нулю, найдем значение базисных переменных:
нулю, найдем значение базисных переменных:  ,
,  ,
,  . Полученное базисное решение
. Полученное базисное решение  очевидно неотрицательно и, следовательно, допустимо. Составим теперь (базисную) симплекс-таблицу в первом столбце, которой указаны имена базисных переменных. (Таблица 3.)
очевидно неотрицательно и, следовательно, допустимо. Составим теперь (базисную) симплекс-таблицу в первом столбце, которой указаны имена базисных переменных. (Таблица 3.)


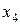


 –5
–5
 4*
4*

 . Наименьшее из этих отношений оказалось во второй строке. Пометим генеральный элемент символом *.
. Наименьшее из этих отношений оказалось во второй строке. Пометим генеральный элемент символом *. запишем число 1, вместо остальных элементов генерального столбца запишем нули, все остальные элементы генеральной строки поделим на генеральный элемент, число 4. В результате мы получим таблицу 4.
запишем число 1, вместо остальных элементов генерального столбца запишем нули, все остальные элементы генеральной строки поделим на генеральный элемент, число 4. В результате мы получим таблицу 4. ,
,  , поэтому в этой клетке следует написать
, поэтому в этой клетке следует написать  ( по формуле 13). В клетке, помеченной знаком (··), напишем
( по формуле 13). В клетке, помеченной знаком (··), напишем  . Аналогично заполняются оставшиеся клетки Таблицы 4. (Таблица 5.)
. Аналогично заполняются оставшиеся клетки Таблицы 4. (Таблица 5.) ,
,  ,
, 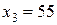 ,
,  ,
,  .
. . То есть на новом базисном плане оно меньше на 35 единиц, чем на первоначальном.
. То есть на новом базисном плане оно меньше на 35 единиц, чем на первоначальном. . Наименьшим из этих отношений оказалось третье и, следовательно, генеральной строкой будет третья строка. Таким образом, генеральным элементом таблицы 5 будет число
. Наименьшим из этих отношений оказалось третье и, следовательно, генеральной строкой будет третья строка. Таким образом, генеральным элементом таблицы 5 будет число  .
.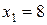 ,
,  ,
,  ,
, 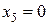
 .
. (14)
(14) можно взять за базисные, тогда все компоненты базисного решения
можно взять за базисные, тогда все компоненты базисного решения  будет неотрицательны.
будет неотрицательны.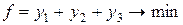 при ограничениях (14) и
при ограничениях (14) и  .
. равно нулю и оно достигается только в том случае, когда значения всех переменных
равно нулю и оно достигается только в том случае, когда значения всех переменных  (15)
(15)
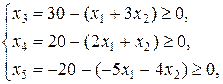
 (18)
(18) .
. взять за базисные, а
взять за базисные, а  , пятая компонента которого отрицательна. То есть это решение будет недопустимым. Следовательно, за базисные мы должны взять какие-то другие переменные.
, пятая компонента которого отрицательна. То есть это решение будет недопустимым. Следовательно, за базисные мы должны взять какие-то другие переменные. в третье уравнение:
в третье уравнение: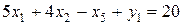
 ,
,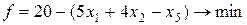
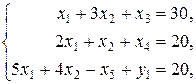
 .
. , которая будет преобразовываться по тем же правилам, что и вся симплекс-таблица.
, которая будет преобразовываться по тем же правилам, что и вся симплекс-таблица.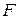
 . Поэтому генеральный элемент будет в третьей строчке и равен 5. После преобразований у нас получиться таблица 8.
. Поэтому генеральный элемент будет в третьей строчке и равен 5. После преобразований у нас получиться таблица 8. ,
,  ,
,  .
. ,
,  ,
,  ,
,  .
.