
|
|
Геометрическое решение задачи линейного программированияФЕДЕРАЛЬНОЕ АГЕНСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ Государственное образовательное учреждение высшего профессионального образования «ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ»
М.М. Луценко
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ РЕШЕНИЕ ЗАДАЧИ
Методические указания и варианты индивидуальных заданий для студентов заочного факультета
САНКТ-ПЕТЕРБУРГ
УДК 512.8
М.М.Луценко
Линейное программирование. Решение задачи. Методические указания и варианты индивидуальных заданий для студентов заочного факультета, – СПб.: Петербургский государственный университет путей сообщения, 2006, 22 с.
Содержание пособия соответствует разделам математического программирования, изучаемым студентами в 3 семестре. Пособие предназначено для студентов специальностей УПП заочного факультета ПГУПС.
Рецензент: профессор В.В. Гарбарук (кафедра «Высшая математика» ПГУПС)
© М.М.Луценко © Петербургский государственный университет Постановка задачи Главным объектом изучения в линейном программирование является задача, которая в наиболее общей форме формулируется следующем образом. Задача. Найти экстремум линейной функции F, если ее аргументы удовлетворяют некоторым ограничениям. Настоящие методические указания посвящены анализу задачи линейного программирования, даны ее различные формы записи и указаны некоторые способы ее решения. Каждый студент должен будет сделать для своей задачи все ниже перечисленные действия. 1. Записать задачу в матричной форме 2. Записать каноническую задачу. 3. Решить задачу геометрически. 4. Найти начальный базисный план с помощью искусственных переменных. 5. Решить задачу симплекс-методом. 6. Написать двойственную задачу к искомой в матричной и развернутой формах. 7. Найти решение двойственной задачи и доказать его оптимальность с помощью теоремы двойственности. Варианты задач и пример решения указаны в конце этих указаний. Матричная и развернутая формы задачи линейного программирования В этом параграфе мы сравним две формы записи задачи линейного программирования. Определение 1. Следующая задача называется стандартной задачей линейного программирования. Задача 1. Найти
где A – матрица системы ограничений, имеющая m строк и n столбцов, b – столбец из m элементов; c, x – столбцы из n элементов. Таким образом, эти матрицы имеют вид
В развернутой форме эта стандартная задача линейного программирования может быть записана в следующем виде. Задача 1’. Найти максимум линейной функции
при ограничениях:
Определение 2. Решением этих задач называется матрица (упорядоченный набор чисел) Определение 3. Линейная функция F задачи 1 называется целевой функцией, а множество D решений системы (2) – множеством допустимых решений (планов) этой задачи. Пример 1. Записать задачу линейного программирования (1), (2) с матрицами
в развернутой форме Решение. В развернутой форме задача формулируется следующим образом. Найти максимум функции
Пример 2. Записать следующую задачу линейного программирования в матричной форме. Минимизировать линейную функцию
Решение.Для того чтобы записать эту задачу в матричной форме (1, 2), изменим неравенства в ограничениях задачи так, чтоб они имели одинаковый знак. Для этого умножим первое неравенство на –1. Мы получим следующую систему ограничений задачи:
Тогда в матричной форме задача примет вид
где
Геометрическое решение задачи линейного программирования Для того чтобы решить задачу линейного программирования геометрически, построим множество решений системы ограничений. Любая прямая Построим теперь линии уровня функции Пример 3. Решить следующую задачу линейного программирования геометрически.
при ограничениях
Решение. Найдем множество
Прямая
Параллельно переместим эту прямую в направлении вектора
Откуда мы находим которое она принимает в точке с координатами 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 Кафедра «Математика и моделирование»
Кафедра «Математика и моделирование»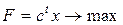 , (1)
, (1)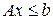 ,
,  , (2)
, (2)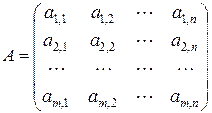 ,
, 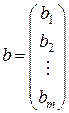 ,
,  ,
, 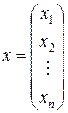 . (3)
. (3)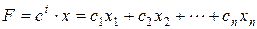 ,
, 

 .
. 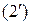
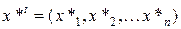 , удовлетворяющая системе ограничений (2) и обеспечивающая максимальное значение функции (1). Иногда это решение называется оптимальным планом задачи. Значение функции на оптимальном плане обозначается
, удовлетворяющая системе ограничений (2) и обеспечивающая максимальное значение функции (1). Иногда это решение называется оптимальным планом задачи. Значение функции на оптимальном плане обозначается 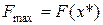 .
.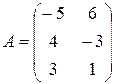 ;
; 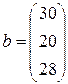 ;
; 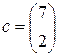 ;
; 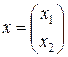
 .
.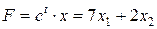 при ограничениях
при ограничениях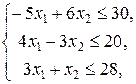
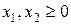 .
.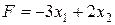 при ограничениях
при ограничениях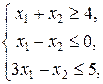
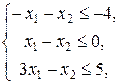
 ,
,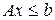 ,
,  ;
; 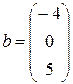 ;
; 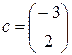 ;
; 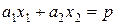 разбивает плоскость на две полуплоскости. Для точек
разбивает плоскость на две полуплоскости. Для точек 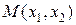 одной из полуплоскостей выполняется неравенство
одной из полуплоскостей выполняется неравенство 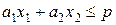 , а для точек другой полуплоскости противоположное неравенство
, а для точек другой полуплоскости противоположное неравенство 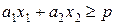 . Если ограничением задачи будет система неравенств, то множеством допустимых решений
. Если ограничением задачи будет система неравенств, то множеством допустимых решений 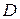 этой задачи будет выпуклое многоугольное множество, полученное как пересечение полуплоскостей, каждая из которых является решением соответствующего неравенства системы.
этой задачи будет выпуклое многоугольное множество, полученное как пересечение полуплоскостей, каждая из которых является решением соответствующего неравенства системы.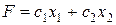 . Очевидно, что это будут параллельные линии
. Очевидно, что это будут параллельные линии 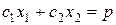 , перпендикулярные нормальному вектору
, перпендикулярные нормальному вектору 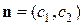 . Следовательно, при параллельном перемещении линии уровня в направлении вектора
. Следовательно, при параллельном перемещении линии уровня в направлении вектора  значение целевой функции F будет возрастать, а противоположном убывать. Свое максимальное значение функция F примет на «последней» общей точке множества допустимых решений и соответствующей линии уровня при ее параллельном переносе в направлении вектора
значение целевой функции F будет возрастать, а противоположном убывать. Свое максимальное значение функция F примет на «последней» общей точке множества допустимых решений и соответствующей линии уровня при ее параллельном переносе в направлении вектора 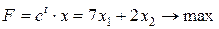 , (4)
, (4)
 разбивает плоскость на две полуплоскости. Стрелочками отметим ту полуплоскости, которая удовлетворяет неравенству
разбивает плоскость на две полуплоскости. Стрелочками отметим ту полуплоскости, которая удовлетворяет неравенству  . Для этого достаточно проверить хотя бы одну точку этой полуплоскости, например, начало координат
. Для этого достаточно проверить хотя бы одну точку этой полуплоскости, например, начало координат 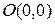 . Пересечение полуплоскостей составит множество допустимых решений задачи D.
. Пересечение полуплоскостей составит множество допустимых решений задачи D. Построим теперь линии уровня функции F, т.е прямые
Построим теперь линии уровня функции F, т.е прямые 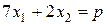 для различных p. На рисунке показана прямая, соответствующая значению
для различных p. На рисунке показана прямая, соответствующая значению  . На части этой прямой, лежащей внутри этой области, значение функции F равно 14.
. На части этой прямой, лежащей внутри этой области, значение функции F равно 14. . Для того чтобы найти ее координаты достаточно решить систему уравнений:
. Для того чтобы найти ее координаты достаточно решить систему уравнений: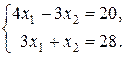
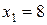 ,
,  . Итак, максимальное на множестве
. Итак, максимальное на множестве 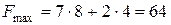 ,
,