
|
|
Приложения дифференциальныхУравнений Пример 1.Составить уравнение кривой, если угловой коэффициент касательной в каждой ее точке равен утроенному квадрату абсциссы точки касания. Доказать, что у= х3+ C, где C - произвольная постоянная, определяет множество кривых с указанным угловым коэффициентом. Из этого множества выделить кривую, проходящую через точку А(1; -2). Решение. По условию задачи угловой коэффициент k касательной к искомой кривой у = у(х) в каждой ее точке равен 3х2. По определению геометрического смысла производной у' = k = 3х2 , или
Умножив обе части полученного дифференциального уравнения на dх, после интегрирования получим
у = х3+ C, (5.24) C – постоянная интегрирования. Итак, семейство кубических парабол удовлетворяет условию задачи. Для доказательства того, что уравнение у = х3+ C определяет множество кривых с указанным угловым коэффициентом, подставим его в исходное дифференциальное уравнение (4.20) (х3+ C)'= 3х2, откуда 3х2º 3х2. Что доказывает справедливость утверждения. Для того, чтобы из бесконечного множества кривых у = х3 + С выбрать ту, что проходит через точку А(1; -2), подставим в выражение (5.24) вместо х и у соответственно 1 и –2, получим -2 = 13+ C, откуда С = -3. Таким образом, уравнение искомой прямой у = х3- 3. Пример 2.В комнате, где температура То = 20оС, некоторое тело остыло за 15 минут с Т1 = 100оС до Т2 = 60оС. Найти закон охлаждения тела. Через сколько минут оно остынет до 40оС. Решение. В силу закона Ньютона (скорость охлаждения пропорциональна разности температур) можно записать
k – коэффициент пропорциональности. То = 20оС, тогда
После интегрирования получим ln(T - 20) = kt + ln|C|, (5.25) откуда T(t) = C ekt+ 20, (5.26) С – произвольная постоянная. Найдем неизвестные С и k, используя начальные условия. Если t = 0, то Т = 100оС и из (5.26) имеем 100 = Сe0 + 20, откуда С = 80. Если t = 15, то Т = 60оС. Подставляя эти значения в (5.25) получим ln 40 = 15k + ln 80, откуда k = Подставляя найденные значения С и k в выражение (5.26), получим закон охлаждения тела T(t) = 20 + 80 или окончательно Т(t) = Найдем время, необходимое для охлаждения тела до T = 40оС, имеем 40 = Таким образом, Пример 3.Установлено, что скорость размножения бактерий в любой момент времени положительна и пропорциональна их массе. Найти закон изменения массы бактерий от времени, если первоначальное их количество составляло 1 г, а, спустя час, оно удвоилось.
Решение. Обозначим через m(t) массу бактерий в момент времени t, тогда
После интегрирования получим m(t) = C ekt, где С – произвольная постоянная. Определим С из условия m = 1 при t = 0, откуда С = 1, т.е. m(t) = ekt. Найдем еk из условия m = 2 при t = 1: 2 = ek. Тогда закон изменения массы бактерий запишется в виде m(t) = 2t. 107. Составить уравнение кривой, если известно, что угловой коэффициент касательной в каждой ее точке равен 4х + 3. 108. Составить уравнение кривой, проходящей через точку А(1; 3), если известно, что угловой коэффициент касательной в каждой ее точке равен 3x2+ 2. 109. Тело, температура которого 25оС погружено в термостат, в котором поддерживается температура 0оС. За какое время тело охладится до 10оС, если за 10 минут оно охлаждается до 20оС? Скорость охлаждения тела пропорциональна температуре тела. 110. Температура вынутого из печи хлеба в течение 20 минут падает с 100 до 60оС. Температура воздуха равна 25оС. Через какое время от начала охлаждения температура хлеба понизится до 30оС? 111. В пивных дрожжах быстрота прироста фермента пропорциональна наличному его количеству m. Первоначальное количество фермента было равно m0. Через 1 час оно удвоилось. Во сколько раз количество фермента возрастет через 3 часа? 112. К началу радиоактивного распада имели 100 г радия. Сколько радия распадается за 200 лет, если период его полураспада равен 1590 годом? 113. Скорость обесценивания оборудования вследствие его износа в данный момент времени пропорциональна его фактической стоимости. Начальная стоимость оборудования равна 10 000 у.е. Какова будет его стоимость через 10 лет, если через 1 год она составляла 9 000 у.е ? 114. Пусть полные издержки С есть функция объема производства х. Найти функцию издержек, если известно, что предельные издержки для всех значений х равняются средним издержкам. 115. Катер движется в спокойной воде со скоростью 18 км/ч. Через 5 минут после выключения двигателя его скорость уменьшилась до 6 км/ч. Определить расстояние, пройденное катером по инерции за 15 минут, если сопротивление воды пропорционально скорости движения катера. 116. Найти класс функций, эластичность которых постоянна и равна k. 117. Эластичность Е= −1/3 для любых значений p. Найти функцию спроса. 118. Пусть функции спроса и предложения на некоторый товар имеют вид D(t) = 30 – p – p׳׳ , S(t) = 20 + p + 3p׳. Найти зависимость равновесной цены p от времени t, если p(0) = 7.
* В данном случае, не нарушая общности, постоянную интегрирования C удобно представить в виде ln|C|. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
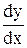 = 3х2. (5.23)
= 3х2. (5.23)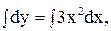
 = k (Т – То),
= k (Т – То),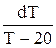 = k dt.
= k dt.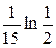 .
.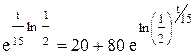 ,
,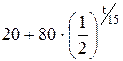 .
.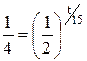 .
.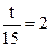 , откуда t = 30 мин.
, откуда t = 30 мин.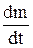 будет скорость размножения этих бактерий. Согласно условию задачи скорость размножения
будет скорость размножения этих бактерий. Согласно условию задачи скорость размножения