
|
|
Уравнения второго порядка с постояннымиКоэффициентами Определение 1. Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида у'' + ру' + qy = 0, (5.18) где р и q – постоянные. Определение 2.Линейной комбинацией функций у1(х) и у2(х) с коэффициентами C1 и C2 называется выражение вида C1 у1(х) + C2 у2(х). Определение 3. Если линейная комбинация C1 у1(х) + C2у2(х) равна нулю, только когда коэффициенты C1 и C2 равны нулю, то функции у1(х) и у2(х) называются линейно независимыми, в противном случае – линейно зависимыми. Общее решение уравнения (5.18) можно найти по его известным частным решениям у1(х) и у2(х). Теорема 1 (о структуре общего решения линейного однородного дифференциального уравнения). Если у1(х) и у2(х) – линейно независимые частные решения уравнения (5.18), то общее решение этого уравнения является линейной комбинацией этих частных решений, т. е. имеет вид у = С1 у1(х) + С2 у2(х), где С1 и С2 – действительные числа. Итак, для нахождения общего решения уравнения (5.18) достаточно найти два его линейно независимых частных решения. Будем искать эти частные решения в виде у = еkх, где k = const; тогда у' = kеkх, у'' = k2еkх. Подставляя эти выражения в уравнение (5.18), получим еkх(k2+ рk + q) = 0. Так как еkх ¹ 0, то k2+ рk + q = 0.(5.19) Это уравнение называется характеристическим уравнением исходного дифференциального уравнения (5.18). Решая характеристическое уравнение (5.19), найдем его корни k1 и k2, а, следовательно, и частные решения уравнения (5.18): у1(х) = Общее решение дифференциального уравнения (5.18) строится в зависимости от характера корней характеристического уравнения. Справедлива теорема. Теорема 2. 1. Пусть характеристическое уравнение (5.19) дифференциального уравнения (5.18) имеет различные действительные корни k1 и k2 (дискриминант D > 0). Тогда общее решение уравнения (5.18) имеет вид у = C1 2. Если характеристическое уравнение (5.19) имеет действительные равные корни k1 = k2 = k (D = 0), то общее решение уравнения (5.18) имеет вид у= 3. Если характеристическое уравнение (5.19) имеет комплексные корни k1 = а + ib и k2 = а – ib (D < 0), здесь i = у = eах(C1 cos bx + C2 sin bx), (5.22) где Здесь C1 и C2 – произвольные постоянные. Пример 1.Найти частные решения следующих уравнений:
1. у'' - 3у' + 2у = 0, у(0) = 3, у'(0) = 4. 2. у'' - 2у' + у = 0, у(0) = 1, у'(0) = 0. 3. у'' - 4у' + 13у = 0, у(0) = 1, у'(0) = 8.
Решение.
1. Составим характеристическое уравнение k2– 3k + 2 = 0, откуда его корни k1 = 1, k2 = 2 (D > 0). Тогда общее решение данного дифференциального уравнения имеет вид у = C1 eх+ C2 e2х. Дифференцируя общее решение, получим: у' = C1 eх+ 2 C2 e2х. Согласно заданным начальным условиям имеем
откуда C1 = 2, C2 = 1. Таким образом, искомым частным решением является функция у = 2 eх+ e2х . 2. Характеристическое уравнение k2– 2k + 1 = 0 имеет при D = 0 действительные и равные корни k1 = k2 = k = 1. Тогда согласно п. 2 Теоремы 2общее решение дифференциального уравнения имеет вид у = eх (C1 + C2 х). Так как у = 1 при х = 0, то C1 = 1 и поскольку у' = eх (C1 + C2х) + C2eхи у' = 0 при х = 0, то C2 = -1. Таким образом, частное решение запишется в виде у = (1 – х) eх. 3. Составляем характеристическое уравнение k2– 4k + 13 = 0 и при D < 0 находим его корни: k1 = 2 + 3i и k2 = 2 – 3i. Здесь а = 2, b = 3, поэтому согласно п.3 Теоремы2 общим решением является функция у = e2х(C1 cos 3x + C2 sin 3x). Учитывая, что у(0) = 1, получим C1 = 1. Продифференцируем общее решение у' = 2у - 3e2х(C1 sin 3x – C2 cos 3x) и учтем, что у'(0) = 8. Тогда получим C2 = 2. Таким образом, приходим к частному решению у = e2х(cos 3x + 2 sin 3x).
Найти решения уравнений
Найти частные решения уравнений
3. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами Пусть дано дифференциальное уравнение y׳׳ + py׳ + qy = f(x), (5.23) где p и q – постоянные действительные коэффициенты, f(x) – заданная функция от х. Теорема.Общее решение неоднородного уравнения (5.23) представляет собой сумму общего решения у0 соответствующего однородного уравнения (5.18) и какого – либо частного решения уч неоднородного уравнения. Отыскание общего решения однородного уравнение осуществляется по правилам, изложенным в п. 2. Таким образом, задача интегрирования уравнения (5.23) сводится к отысканию частного решения уч неоднородного уравнения. В общем случае интегрирование уравнения (5.23) может быть осуществлено методом вариации произвольных постоянных. Для правых частей (5.23) специального видачастное решение находится методом подбора. Пример.Найти общее решение дифференциального уравнения у׳׳ − 4у׳ + 3у = 6. Решение. Найдем общее решение однородного уравнения у׳׳− 4у׳ + 3у = 0. Корни характеристического уравнения k2 – 4k + 3 = 0 (D > 0) k1 = 1, k2 = 3. Общее решение однородного уравнения имеет вид у0 = С1е х + С2е3х Частное решение неоднородного уравнения будем искать в виде уч = С (С – постоянная). Подставим С в исходное уравнение С׳׳ − 4С׳ + 3С = 6, откуда С = 2, т.е. уч = 2. Общее решение данного неоднородного уравнения, равное сумме у0 и уч , запишется в виде у = С1ех +Се3х + 2. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ; у2(х) =
; у2(х) =  .
. . (5.20)
. (5.20)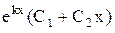 .(5.21)
.(5.21) - мнимая единица, а, b ¹ 0 – действительные числа, то общее решение уравнения (5.18) имеет вид
- мнимая единица, а, b ¹ 0 – действительные числа, то общее решение уравнения (5.18) имеет вид .
.
 = 0, у'
= 0, у' 
 = 2, у'
= 2, у'  = 0
= 0
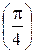 = 1
= 1