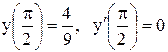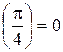|
|
Дифференциальные уравненияГЛАВА V. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ Основные понятия и определения Определение 1. Дифференциальным уравнением называется уравнение, связывающее независимую переменную х, искомую функцию у = у(х) и ее производные у', у'',…, у(n), т. е. уравнение вида F(х; у; у'; у'';…; у(n)) = 0. Дифференциальное уравнение называется обыкновенным, если искомая функция у = у(х)есть функция одной независимой переменной х. Определение 2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в него. Определение 3. Решением дифференциального уравнения n-го порядка на интервале (а; b) называется функция у = j(х), определенная на интервале (а; b) вместе со своими производными до n-го порядка включительно, которая будучи подставлена в дифференциальное уравнение обращает его в тождество, т.е.
F(x; j(х); j'(х);…; j(n)(х)) º 0.
Дифференциальные уравнения Первого порядка. Определение 1.Дифференциальным уравнением первого порядка называется уравнение вида: F(x; у; у') = 0. (5.1) Если уравнение (5.1) удается разрешить относительно у', то получится у' = f(x; у) (5.2) уравнение первого порядка, разрешенное относительно производной. Иногда дифференциальные уравнения первого порядка записывают в дифференциалах j(х; у) dх + g(x; у) dу = 0.
Определение 2.Общим решениемдифференциального уравнения первого порядка называется функция у = j(х; C), зависящая от одной произвольной постоянной C и удовлетворяющая данному дифференциальному уравнению при любых допустимых значениях C. Соотношение вида Ф(х; у; С) = 0, неявно определяющее общее решение, называется общим интегралом дифференциального уравнения. Определение 3.Частным решением дифференциального уравнения называется решение, полученное из общего решения при каком-либо определенном значении постоянной С = С0, т.е. у = j(х; С0). Соотношение, получаемое из общего интеграла при конкретном значении постоянной С, называется частным интегралом дифференциального уравнения. С геометрической точки зрения совокупность всех решений дифференциального уравнения представляет собой совокупность кривых, называемых интегральными кривыми, а каждое частное решение представляет отдельную интегральную кривую. Определение 4. Задача нахождения частного решения дифференциального уравнения, удовлетворяющего заданным начальным условиям, называется задачей Коши. Задачей Коши в случае дифференциального уравнения первого порядка называют задачу нахождения решения у = у(х) уравнения у '= f(x; y), удовлетворяющего начальному условию у(х0) = у0 (
1. Дифференциальные уравнения с разделяющимися Переменными Определение 5. Уравнение вида j(у) dу = g(x) dx называется дифференциальным уравнением с разделенными переменными. Решение этого уравнения находится путем интегрирования обеих его частей. В результате чего его общий интеграл представляется в виде F(y) = G(x) + C. Определение 6. Уравнение вида у' = j(у) g(x)называется дифференциальным уравнением с разделяющимися переменными. Решение дифференциального уравнения с разделяющимися переменными находится с помощью следующего алгоритма: 1. Заменить производную у' отношением дифференциалов
2. Умножить обе части уравнения на dх dу = j(у) g(x) dх. 3. Разделить переменные, т. е. распределить их так, чтобы функция, зависящая от у, располагалась при дифференциале dу, а функция, зависящая от х, при дифференциале dх. Для этого последнее уравнение необходимо разделить на j(у). Получим 4. Проинтегрировать обе его части F(у) = G(x) + C – общий интеграл дифференциального уравнения. 5. Найти частный интеграл (решение), если задано начальное условие у(х0) = у0. F(y) = G(x) + C0. Пример 1. Решить дифференциальное уравнение х у у' + 1 + х2= 0, если у(1) = 1. Решение.Данное уравнение является дифференциальным уравнением с разделяющимися переменными. Решим его, используя предложенный алгоритм. 1. х у 2. х у dу + (1 + х2) dх = 0. 3. Разделим переменные, для чего разделим уравнение на х (х ¹ 0) у dy = - 4. Проинтегрируем обе части уравнения
Преобразуя это выражение, получим общий интеграл в виде x = С 5. Найдем частный интеграл, используя начальное условие у = 1 при х =1. 1 = С e-1, C = e. Откуда х =
Решить дифференциальные уравнения:
1. (1 + у) dх – (1 – х) dу = 0 2. х2у' + у = 0 3. (ху2+ х) – (у – х2у) у' = 0 4. х2у' + у – 1 = 0 5. (1 + у2) dх = (1 + х2) dу 6. (1 + 2у) х dх + (1 + х2) dу = 0 7. ху (1 + х2) у' = 1 + у2 8. eу(1 + х2) у' = 2х (1 + eу) 9. у – ху' = 1 + х2у' 10. cos x sin y dy = cos y sin x dx 11. 12. х2у' - 2ху = 3у 13. (ху + у)
Найти частные решения дифференциальных уравнений
14. х2 dх + у dу = 0, если у = 1 при х = 0 15. (1 + х2) у' = 2х (у + 3), если у = -1 при х = 0 16. (1 + х) у dх = (у – 1) dу, если у = 1 при х = 1 17. 2у' 18. х2у' + у2= 0, если у = 1 при х = -1 19. у' = (2у + 1) ctg x, если у = 20. у' tg x = 1 + у, если у = - 21. (1 + eх) у у' = eх, если у = 1 при х = 0 22. у' 23. ху' = 24. у' tg x – y = 1, если у = 1 при х =
2. Однородные дифференциальные уравнения Первого порядка Определение 7. Функция f(x; у) называется однородной функцией своих аргументов k-го измерения (k-й степени), если при любом t имеет место тождество f(tx; ty) = tk f(x; у). Например, функция f(x; у) = х2у – ху2является однородной функцией третьего измерения, т. к. f(tx; ty) = (tx)2ty – tx (ty)2= t3( x2y – xy2) = t3f(x; у). При k = 0 имеем функцию нулевого измерения, примером которой является функция f(x; у) = f(tx; ty) = Определение 8. Дифференциальное уравнение первого порядка у' = f(x; y) называется однородным, если f(x; y) – однородная функция нулевого измерения. Данное уравнение можно представить в виде P(x; у) dх + Q(x; у) dy = 0, (5.3) где P(x; y) и Q(x; y) – однородные функции одного измерения. Однородные дифференциальные уравнения первого порядка приводятся к дифференциальным уравнениям с разделяющимися переменными с помощью подстановки у = z x, где z = z(x) – новая неизвестная функция переменной х. Пример 1. Решить дифференциальное уравнение (х2– 2у2) dх + ху dу = 0. Решение. Сопоставим данное уравнение с уравнением (5.3). Здесь P(x; y) = x2- 2y2и Q(x; y) = xy – однородные функции второго измерения. Действительно P(tx; ty) = (tx)2 - 2(ty)2= t2(x2 - 2y2) = t2 P(x; y), k = 2; Q(tx; ty) = tx ty = t2 x y = t2Q(x; у), k = 2. Следовательно, данное уравнение является однородным дифференциальным уравнением первого порядка. Положим у = z x, откуда dу = (z x)' dх = (z' x + z) dх = x Подставим эти выражения у и dу в исходное уравнение. (х2 - 2z2x2) dх + x z x (x dz + z dх) = 0, откуда после раскрытия скобок и приведения подобных получим х2(1 – z2) dх + x3 z dz = 0. Видим, что в результате произведенной замены, получено дифференциальное уравнение с разделяющимися переменными. Разделим в нем переменные, поделив обе его части на х3(1 - z2). Тогда
Для удобства умножим обе части последнего уравнения на 2 и проинтегрируем
ln х2= ln |С| |z2– 1|. Отсюда х2 = C (z2– 1), а обратная замена z = х2= C Пример 2. Решить дифференциальное уравнение ху' = Решение . Разделим обе части уравнения на х и перепишем его в виде у' = Полученное уравнение соответствует определению однородного дифференцированного уравнения первого порядка у' = f(x; y), здесь f(x; y) = Разделим переменные, поделив обе части на
Отсюда после интегрирования находим arcsin z = ln|х| + ln|С|, или arcsin z = ln|Cх|. Заменяя z на Отсюда общее решение: у= х sin ln|Сх|. При разделении переменных мы делили обе части уравнения на Положим
Решить дифференциальные уравнения:
25. (х – у) dх + х dу = 0 26. (х – у) у dх – х2 dу = 0 27. (х2– 2ху) у' = ху – у2 28. х3 dу – у (х2+ у2) dх = 0 29. 30. 2 х у у' + х2- 2у2= 0 31. х у у' = х2+ у2 32. х у' - у =
Найти частные решения дифференциальных уравнений:
33. у' х – у + х = 0, если у = 0 при х = 1 34. х у2у' = х3+ у3, если у = 3 при х = 1 35. у2 dх = (х у – х2) dу, если у =1 при х = 1 36. х2у' = ху + у2, если у = 1 при х = 1 37. ху + у2= (2х2+ ху) у', если у = 1 при х = 1 38. у' (х2+ ху) = у2, если у = 2 при х = 2.
3. Линейные дифференциальные уравнения Первого порядка Определение 9. Линейным дифференциальным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной. Оно имеет вид
у' + Р(х)у = Q(x), (5.4)
где Р(х) и Q(x) – заданные функции переменной х. Если Q(x) º 0, то уравнение (5.4) называется линейным однородным. Оно является уравнением с разделяющимися переменными и имеет общее решение у = С− произвольная постоянная.
Общее решение неоднородного уравнения можно найти методом вариации произвольной постоянной (метод Лагранжа), который состоит в том, что решение уравнения (5.4) записывается в виде у = где С(х) – новая неизвестная функция переменной х. Пример 1. Решить дифференциальное уравнение у' + 2ху = 2х Решение. Применим метод вариации произвольной постоянной. Рассмотрим однородное уравнение у' + 2ху = 0, соответствующее данному неоднородному. Это дифференциальное уравнение с разделяющимися переменными. Найдем его общее решение, используя алгоритм, рассмотренный в §3.
dу + 2 х у dх = 0 . Разделим переменные, поделив последнее уравнение на у,
В результате почленного интегрирования получим
ln|у| + х2+ ln|С1| = 0, или ln|уС1| = -х2. После потенцирования имеем у = С Общее решение неоднородного уравнения ищем в виде у = С(х)
где С(х) – неизвестная функция переменной х. Подставим данное выражение для у в исходное неоднородное дифференциальное уравнение.
После дифференцирования и несложных преобразований получим дифференциальное уравнение относительно неизвестной функции С(х):
Откуда после интегрирования имеем С(х) = х2+ C. Итак, общее решение неоднородного уравнения будет у = (х2+ C) где C– постоянная интегрирования. Существует другой метод (метод Бернулли)решения дифференциального уравнения (5.4), согласно которому нахождение его общего решения сводится к решению двух дифференциальных уравнений с разделяющимися переменными с помощью подстановки у = u∙ v, (5.5) где u и v – неизвестные функции от х. Дифференцируя (4.5), находим yʹ = (uv)ʹ = uʹv + uvʹ.(5.6) Подставив значения у и у' в уравнение (5.4), получим vuʹ + uvʹ + P(x)uv = Q(x) или v(uʹ + P(x)u) + uvʹ = Q(x). Так как искомая функция у подстановкой (5.5) представлена в виде произведения двух неизвестных функций u и v, то одну из них, например, u мы можем выбрать по нашему усмотрению, кроме u = 0. Выберем u так, чтобы uʹ + P(x)u = 0 (5.8) Решая это уравнение как уравнение с разделяющимися переменными, найдем функцию u = u(x). Найденную функцию подставим в уравнение (5.7). u(x)vʹ = Q(x).(5.9) Это уравнение с разделяющимися переменными, решая которое находим функцию v = v(x; C), содержащую произвольную постоянную C и являющуюся общим решением уравнения (5.9). Заменив в равенстве (5.5) у = uv функции u и v найденными значениями, получим общее решение исходного дифференциального уравнения у = u(x) v(x; C). Частное решение находим, используя начальные условия. Пример 2. Найти частное решение дифференциального уравнения х (х – 1) у' + у = х2(2х – 1), у(2) = 4. Решение. Данное уравнение является линейным дифференциальным уравнением первого порядка. Действительно, в результате деления обеих его частей на x (х – 1) (х ¹ 0; х ¹ 1) оно преобразуется к виду уравнения (5.4). у' + Найдем общее решение преобразованного дифференциального уравнения с помощью подстановки у = u v. При этом у' = u' v + u v'. Подставляя у и у' в уравнение (4.10), получим u' v + u v' + или v Поскольку неизвестная функция у представлена в виде произведения двух: u и v, то одну из них, например, u можно выбрать по нашему усмотре- нию. Выберем u так, чтобы выражение в скобках обратилось в нуль, т. е.
Тогда уравнение (5.11) примет вид
Решаем уравнение (5.12) как дифференциальное уравнение с разделяющимися переменными:
Раскладывая дробь в правой части последнего уравнения после интегрирования получим одно из его частных решений
или Подставив найденную функцию u(x) в уравнение (5.13), придем к дифференциальному уравнению относительно функции v.
интегрируя которое, получим v(x; C) = х2– х + C. (5.15) Заменив в подстановке у = u v функции u и v их выражениями из равенств (5.14) и (5.15), получим искомое общее решение данного дифференциального уравнения
Найдем частное решение, удовлетворяющее начальному условию у = 4 при х = 2. 4 = Следовательно, искомым частным решением является функция у = х2. Решить дифференциальные уравнения:
Найти частные решения дифференциальных уравнений:
Дифференциальные уравнения Второго порядка Дифференциальное уравнения второго порядка в общем случае записывается в виде F(x; у; у'; у'') = 0.(5.16)
Для этих уравнений остается справедливым определение общего решения (интеграла), с той лишь разницей, что теперь оно будет содержать две произвольные постоянные:
у = j(х; C1; C2) – общее решение;
Ф(х; у; C1; C2) = 0 – общий интеграл.
Задача Коши для дифференциальных уравнений второго порядка формулируется следующим образом: найти решение у = у(х) уравнения (5.16), удовлетворяющее начальным условиям
где
1. Дифференциальные уравнения, допускающие Понижение порядка Эти уравнения имеют вид у'' = f(x), (5.17) где f(x) – заданная функция. Данные уравнения решаются путем двукратного интегрирования. Понизим порядок уравнения, полагая у' = z , тогда у'' = z' и уравнение (5.17) принимает вид z' = f(x) или z = где F(х) – одна из первообразных для функции f(x); C1 – постоянная интегрирования. Так как z = y', то у' = F(x) + C1, или dу = F(x) dx + C1 dx. Отсюда, интегрируя еще раз, получим общее решение уравнения (5.17) y = G(x) + C1x + C2 . Пример 1.Решить дифференциальное уравнение у'' = e2х, если у(0) = 0; у'(0) = 0. Решение. Положим у' = z , тогда у'' = z' и, следовательно, z' = e2х, или Умножая обе части этого уравнения на dх, после интегрирования получим:
Осуществляя обратную замену: z = y', имеем у' = Разделим переменные и проинтегрируем второй раз, тогда получим общее решение исходного уравнения у = Для решения задачи Коши воспользуемся начальными условиями: у = 0 при х = 0 и у' = 0 при х = 0. Поставляя эти значения в выражения для у и у', получим два уравнения относительно неизвестных C1 и C2.
Искомое частное решение уравнения имеет вид у = Найти общие решения уравнений:
Найти частные решения уравнений:
2. Линейные однородные дифференциальные 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
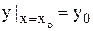 ), где х0, у0 - заданные числа.
), где х0, у0 - заданные числа.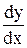
 .
.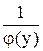 dу = g(x) dх – уравнение с разделенными переменными.
dу = g(x) dх – уравнение с разделенными переменными. ;
; .
.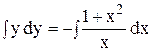 ,
, *, С ¹ 0.
*, С ¹ 0.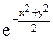 .
.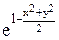 .
.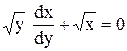
 = 1
= 1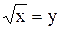 , если у = 1 при х = 4
, если у = 1 при х = 4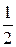 при х =
при х = 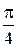
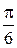
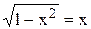 , если у = 0 при х = 1
, если у = 0 при х = 1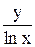 , если у = 1 при х = e
, если у = 1 при х = e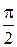
 . Действительно
. Действительно .
. dх + z dх = x dz + z dх.
dх + z dх = x dz + z dх.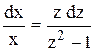 .
.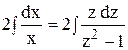 ;
; = ln|z2– 1| + ln|С|, или
= ln|z2– 1| + ln|С|, или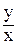 приводит к результату
приводит к результату , или х4= C (у2– х2).
, или х4= C (у2– х2).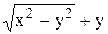 .
.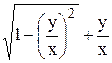 .
. , или у = z x, тогда у' = x z' + z. Подставляя в уравнение выражения для у и у', получим
, или у = z x, тогда у' = x z' + z. Подставляя в уравнение выражения для у и у', получим  , или x dz =
, или x dz = 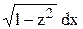 .
.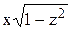 ,
,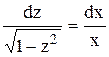 .
.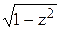 = 0 (х ¹ 0), откуда у = ±х. Непосредственная проверка показывает, что функции у = х и у = -х также являются решениями исходного уравнения.
= 0 (х ¹ 0), откуда у = ±х. Непосредственная проверка показывает, что функции у = х и у = -х также являются решениями исходного уравнения.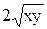 - у + х у' = 0
- у + х у' = 0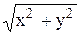
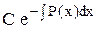 ,
,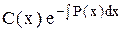 ,
, .
. + 2х dх = 0.
+ 2х dх = 0.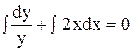 ;
;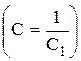 .
.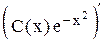 + 2х С(х)
+ 2х С(х) 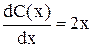 .
. ,
, (5.7)
(5.7) . (4.10)
. (4.10)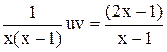 ,
, . (5.11)
. (5.11)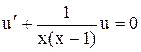 . (5.12)
. (5.12)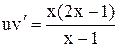 . (5.13)
. (5.13)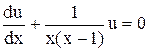 ,
, .
.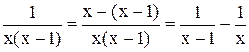 ,
,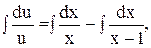
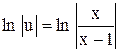 ,
, . (5.14)
. (5.14) ,
, ,
, (х2– х + С).
(х2– х + С).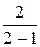 (4 - 2 + С), т. е. С = 0.
(4 - 2 + С), т. е. С = 0.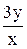 = x
= x
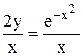

 = 0
= 0
 ,
,

 ,
,
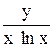 = х ln x,
= х ln x,

 или
или 
 - заданные числа.
- заданные числа. f(x), откуда dz = f(x) dx. После интегрирования обеих частей получим
f(x), откуда dz = f(x) dx. После интегрирования обеих частей получим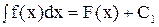 ,
, .
. ,
,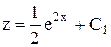 .
. .
.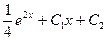 .
.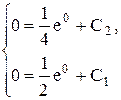 откуда
откуда 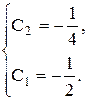
 .
.