
|
|
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Согласно номеру своего варианта выберите условие задачи и постройте ее модель. 2. Найдите оптимальное решение задачи в Excel и продемонстрируйте его преподавателю. Примечание 2.1. Расчет числовых данных, которые непосредственно не заданы в условии задачи, производите непосредственно в ячейках экранной формы. Например, для ввода коэффициента 3. Оформите отчет по лабораторной работе, который должен содержать: · титульный лист (рис.2.1); · исходные данные варианта; · построенную модель задачи с указанием всех единиц измерения; · результаты решения задачи.
Рис.2.1. Пример оформления титульного листа отчета по лабораторной работе 2.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] Если в какой-либо системе (экономической, организационной, военной и т.д.) имеющихся в наличии ресурсов не хватает для эффективного выполнения каждой из намеченных работ, то возникают так называемые распределительные задачи. Цель решения распределительной задачи – отыскание оптимального распределения ресурсов по работам. Под оптимальностью распределения может пониматься, например, минимизация общих затрат, связаных с выполнением работ, или максимизация получаемого в результате общего дохода. Для решения таких задач используются методы математического программирования. Математическое программирование – это раздел математики, занимающийся разработкой методов отыскания экстремальных значений функции, на аргументы которой наложены ограничения. Слово "программирование" заимствовано из зарубежной литературы, где оно используется в смысле "планирование". Наиболее простыми и лучше всего изученными среди задач математического программирования являются задачи линейного программирования. Характерные черты задач ЛП следующие: 1) показатель эффективности L представляет собой линейную функцию, заданную на элементах решения 2) ограничительные условия, налагаемые на возможные решения, имеют вид линейных равенств или неравенств. В общей форме записи модель задачи ЛП имеет вид:
Допустимое решение – это совокупность чисел Оптимальное решение– это план Для построения математической модели необходимо ответить на следующие три вопроса. 1. Что является искомыми величинами, то есть переменными этой задачи? 2. В чем состоит цель, для достижения которой из всех допустимых значений переменных нужно выбрать те, которые будут соответствовать наилучшему, то есть оптимальному, решению? 3. Какие ограничения должны быть наложены на переменные, чтобы выполнялись условия, описанные в задаче? В данной лабораторной работе рассматривается одноиндексная задача ЛП, представляющая собой общую распределительную задачу, которая характеризуется различными единицами измерения работ и ресурсов. Рассмотрим следующую задачу (вариант 0 из табл.2.1). Постановка задачи Мебельный комбинат выпускает книжные полки А из натурального дерева со стеклом, полки B1 из полированной ДСП (древесно-стружечной плиты) без стекла и полки B2 из полированной ДСП со стеклом. Габариты полок А, B1 и В2 следующие: длина 1100 (d) мм, ширина 250 (w) мм, высота 300 (h) мм (рис.2.2). Размер листа ДСП
Рис.2.2. Габариты полок, выпускаемых мебельным комбинатом
При изготовлении полок А выполняются следующие работы: столярные, покрытие лаком, сушка, резка стекла, упаковка. Все операции, производимые в ходе столярных работ и упаковки, выполняются вручную. Полки B1 и В2 поставляются в торговую сеть в разобранном виде. За исключением операции упаковки, все остальные операции (производство комплектующих полки, резка стекла) при изготовлении полок B1 и В2, выполняются на специализированных автоматах. Трудоемкость столярных работ по выпуску одной полки А составляет 4 (Тр1) ч. Производительность автомата, покрывающего полки А лаком – 10 (Пр1) полок в час, автомата, режущего стекло – 100 (Пp2) стекол в час. Сменный фонд времени автомата для покрытия лаком – 7 (ФВ1) ч, автомата для резки стекла – 7,5 (ФВ2) ч. Сушка полок, покрытых лаком, происходит в течение суток в специальных сушилках, вмещающих 50 (V1) полок. На упаковку полки А требуется 4 (Тр2) минуты. В производстве полок заняты 40 (Р1) столяров и 14 (Р2) упаковщиков. Производительность автомата, производящего комплектующие полок B1 и В2, равна 3 (Пр3) полки в час, а его сменный фонд времени равен 7,4 (ФВ3) ч, трудоемкость упаковочных работ составляет 8 (Тр3) мин для полки В1 и 10 (Тр4) мин для полки В2. От поставщиков комбинат получает в месяц 400 (Z1) листов полированной ДСП, 230 (Z2) листов ДВП (древесно-волокнистой плиты), а также 260 (Z3) листов стекла. Из каждого листа ДВП можно выкроить 14 (К1) задних стенок полок B1 и В2, а из каждого листа стекла – 10 (К2) стекол для полок А и В2. Склад готовой продукции может разместить не более 350 (V2) полок и комплектов полок, причем ежедневно в торговую сеть вывозится в среднем 40 (N) полок и комплектов. На начало текущего месяца на складе осталось 100 (Ост) полок, произведенных ранее. Себестоимость полки А равна 205 (C1) руб., полки В без стекла – 142 (C2) руб., со стеклом – 160 (С3) руб. Маркетинговые исследования показали, что доля продаж полок обоих видов со стеклом составляет не менее 60% (Д) в общем объеме продаж, а емкость рынка полок производимого типа составляет около 5300 (V3) штук в месяц. Мебельный комбинат заключил договор на поставку заказчику 50 (З) полок типа В2 в текущем месяце. Составьте план производства полок на текущий месяц. Известны цены реализации полок: полка А – 295 (Ц1) руб., полка В без стекла – 182 (Ц2) руб., полка В со стеклом – 220 (Ц3) руб. Построение модели I этап построения модели заключается в определении (описании, задании, идентификации) переменных. В данной задаче искомыми неизвестными величинами является количество полок каждого вида, которые будут произведены в текущем месяце. Таким образом, II этап построения модели заключается в построении целевой функции, представляющей цель решения задачи. В данном случае цель – это максимизация прибыли, получаемой от продажи полок всех видов в течение месяца. Поскольку в этой задаче прибыль может быть определена как разность между ценой (Ц1, Ц2, Ц3) и себестоимостью (С1, С2, С3), то ЦФ имеет вид
III этап построения модели заключается в задании ограничений, моделирующих условия задачи. Все ограничения рассматриваемой задачи можно разделить на несколько типов. Ограничения по фонду времени (с использованием трудоемкости работ)
Левая часть ограничений по фонду времени представляет собой время, затрачиваемое на производство полок в течение месяца в количестве
Примечание 2.2. Важным моментом проверки правильности составления ограничений является проверка совпадения единиц измерения левой и правой частей ограничения. В ограничении (2.2) левая и правая части измеряются в часах, потраченных на выпуск продукции в течение месяца. Аналогично записывается ограничение (2.3) по фонду времени на упаковочные работы, в котором 14 чел. (Р2) – это количество упаковщиков:
Ограничения по фонду времени (с использованием производительности работ) Неравенство (2.4) описывает ограничение по фонду времени на покрытие лаком полок типа А. Отличие ограничений, учитывающих данные о производительностиработ, от ограничений, учитывающих данные отрудоемкости работ, состоит в том, что производительность необходимо преобразовать в трудоемкость. Трудоемкость является величиной, обратной производительности. Коэффициент
Неравенство (2.5) описывает ограничение по фонду времени на резку стекла для полок типа А и В2:
Неравенство (2.6) описывает ограничение по фонду времени на производство комплектующих полок типа В1 и В2:
Ограничения по запасу расходуемых в производстве материалов (по запасу используемых для производства полок деталей)
Неравенство (2.7) описывает ограничение по запасу листов ДСП, поставляемых на комбинат ежемесячно. При этом следует учесть, что из листа ДСП надо выкраивать комплекты (верхнюю и нижнюю стороны полок, 2 боковые стороны) для производства полок. Поэтому при задании ограничения имеет смысл ориентироваться не на количество листов ДСП, а на количество комплектов для полок [правая часть (2.7)], которые можно получить из имеющегося запаса ДСП. Но поскольку листы ДСП можно раскраивать различными способами и получать при этом различное количество деталей и комплектов, то обозначим месячный запас комплектов в правой части (2.7) как
Аналогично ограничению по ДСП неравенство (2.8.) – это ограничение по запасу задних стенок из ДВП для полок В1 и В2, а неравенство (2.9) – ограничение по запасу стекол для полок А и В2. В отличие от ДСП листы ДВП и листы стекла кроятся стандартным способом, и из каждого листа ДВП получается 14 (К1) задних стенок полок, а из каждого листа стекла получается 10 (К2) стекол. Ежемесячный запас листов ДВП и стекла составляет соответственно 230 (Z2) и 260 (Z3). При составлении левых частей ограничений (2.8) и (2.9) следует учесть, что на каждую полку В1 и В2 приходится по одной задней стенке, а на каждую полку А и В2 – по 2 стекла:
Ограничения по емкости вспомогательных помещений и рынка
Неравенство (2.10) является ограничением по количеству полок А, которые может вместить сушилка. В правой части (2.10) представлено количество полок, которые могут быть просушены в течение месяца (в день может быть просушено 50 (V1) полок):
Неравенство (2.11) описывает ограничение по количеству полок всех видов, которые может вместить склад готовой продукции. При этом правая часть (2.11) учитывает, что общая емкость склада уменьшена на 100 (Ост) полок, которые остались невывезенными с прошлого месяца. Кроме того, в течение месяца каждый день будет освобождаться по 40 (N) мест для полок:
Неравенство (2.12) описывает ограничение по примерной емкости рынка, равной 5300 (V3) полкам всех видов:
Ограничения по гарантированному заказу
Неравенство (2.13) показывает, что необходимо произвести как минимум 50 (З) заказанных полок В2, а возможно, и большее количество, но уже для свободной продажи:
Ограничения по соотношению объемов продаж различных товаров
Неравенство (2.14) показывает, что доля полок А и В2 в общем объеме полок, производимых для свободной продажи, должна составлять не менее 60% (Д). К такому выводу приводят результаты маркетинговых исследований. Поскольку из всех полок В2 в свободную продажу поступит лишь
Определение количества комплектов для полок В1 и В2 Рассмотрим подробно вопрос определения максимально возможного количества комплектов для полок В1 и В2, которое можно произвести из ежемесячного запаса ДСП. В зависимости от размеров листов ДСП ( Согласно 1-му варианту из одного листа ДСП для полок В1 и В2 можно выкроить 19 деталей верхней или нижней стенок, а также 9 деталей боковых стенок. По 2-му варианту раскроя получаем 12 деталей верхней или нижней стенок и 36 деталей боковых стенок. По 3-му варианту раскроя получаем 16 деталей верхней или нижней стенок и 18 деталей боковых стенок. Обозначим количество листов ДСП, раскроенных в течение месяца: по 1-му варианту через
Рис.2.3. Возможные варианты раскроя листов ДСП Количество всех раскроенных листов ДСП не должно превышать 400 (Z1), то есть ежемесячный запас их на складе:
При этом, поскольку в каждый комплект входит одна верхняя и одна нижняя стенки, количество нижних и верхних стенок, получаемых при раскрое всех листов ДСП [левая часть (2.16)], должно быть не меньше чем
Аналогичный смысл имеет ограничение (2.17), которое задает нижнюю границу количества боковых стенок полок:
После преобразования описанных неравенств получим модель задачи (2.18), позволяющую раскроить максимальное количество комплектов:
Таким образом, при решении задачи (2.18) симплекс-методом (например, в MS Excel) переменная
Решив задачу (2.19), получаем
то есть в текущем месяце необходимо произвести 1100 полок А и 120 полок В2, а производство полок В1 нецелесообразно. После реализации всех произведенных полок комбинат получит прибыль в размере 106 200 рублей. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 1. Что такое распределительная задача, общая распределительная задача? 2. Что такое математическое и линейное программирование? 3. Какова общая форма записи модели ЛП? 4. Что такое допустимое и оптимальное решения? 5. Каковы основные этапы построения математической модели ЛП? 6. Каков экономический смысл и математический вид ЦФ задачи о производстве полок? 7. Как можно классифицировать ограничения задачи о полках по их экономическому смыслу? 8. Чем отличается построение ограничений, использующих данные о трудоемкости и производительности работ? 9. Объясните способ построения каждого конкретного ограничения задачи о полках. 10. Каким образом решается задача оптимального раскроя листов ДСП? 11. Каким образом единицы измерения параметров задачи используются для выявления ошибок построения ограничений?

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 при
при  в левой части (2.3) в соответствующую ячейку надо ввести выражение =4/60, после чего в ячейке отобразится результат вычисления, то есть 0,066666667. Для ввода правой части ограничения (2.3) в соответствующую ячейку надо ввести выражение =14*8*1*22, при этом в ячейке отобразится число 2464. Этот способ позволяет четко представлять путь получения числовых данных в ячейках экранной формы, избегать ошибок при расчете параметров задачи, а также обеспечивает высокую точность расчетов.
в левой части (2.3) в соответствующую ячейку надо ввести выражение =4/60, после чего в ячейке отобразится результат вычисления, то есть 0,066666667. Для ввода правой части ограничения (2.3) в соответствующую ячейку надо ввести выражение =14*8*1*22, при этом в ячейке отобразится число 2464. Этот способ позволяет четко представлять путь получения числовых данных в ячейках экранной формы, избегать ошибок при расчете параметров задачи, а также обеспечивает высокую точность расчетов. ;
; ;
при ограничениях
;
при ограничениях

 , удовлетворяющих ограничениям задачи (2.1).
, удовлетворяющих ограничениям задачи (2.1). , при котором ЦФ принимает свое максимальное (минимальное) значение.
, при котором ЦФ принимает свое максимальное (минимальное) значение. м.
м.
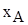 – количество полок А (шт./мес.);
– количество полок А (шт./мес.);  – количество полок В1 (шт./мес.);
– количество полок В1 (шт./мес.);  – количество полок В2 (шт./мес.).
– количество полок В2 (шт./мес.).

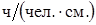 – количество часов работы одного человека в течение смены; 1 см./дн. – количество смен в одном рабочем дне; 22 дн./мес . – количество рабочих дней в месяце (табл.2.1):
– количество часов работы одного человека в течение смены; 1 см./дн. – количество смен в одном рабочем дне; 22 дн./мес . – количество рабочих дней в месяце (табл.2.1):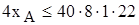




 (
(  ) при
) при 





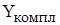 и рассмотрим способ его численного определения позже. В левой части ограничения (2.7) задается количество комплектов (по одному на полку), необходимых на производство полок в течение месяца в объеме
и рассмотрим способ его численного определения позже. В левой части ограничения (2.7) задается количество комплектов (по одному на полку), необходимых на производство полок в течение месяца в объеме 








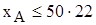




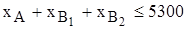

 , то это учитывается при составлении ограничения (2.14), которое после алгебраических преобразований принимает вид (2.15).
, то это учитывается при составлении ограничения (2.14), которое после алгебраических преобразований принимает вид (2.15).
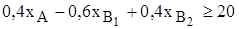
 мм) и габаритов полок (
мм) и габаритов полок (  мм) детали полок В1 и В2 можно выкроить различными способами. Рассмотрим три возможных варианта такого раскроя, представленные на рис.2.3 (затемненные участки – это неиспользованная площадь ДСП).
мм) детали полок В1 и В2 можно выкроить различными способами. Рассмотрим три возможных варианта такого раскроя, представленные на рис.2.3 (затемненные участки – это неиспользованная площадь ДСП). (лист./мес.); по 2-му варианту -
(лист./мес.); по 2-му варианту -  (лист./мес.); по 3-му варианту –
(лист./мес.); по 3-му варианту –  (лист./мес.). При производстве полок нам выгодно стремиться к такому раскрою листов ДСП, при котором из полученных деталей можно укомплектовать максимальное количество полок. Количество комплектов, получаемых из раскроенных деталей, мы ранее обозначили через
(лист./мес.). При производстве полок нам выгодно стремиться к такому раскрою листов ДСП, при котором из полученных деталей можно укомплектовать максимальное количество полок. Количество комплектов, получаемых из раскроенных деталей, мы ранее обозначили через 



 :
:



 ;
;


 шт./мес.,
шт./мес.,  шт./мес.,
шт./мес., 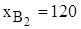 шт./мес.,
шт./мес.,
 руб./мес.,
руб./мес.,