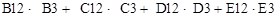|
|
Формулы, описывающие ограничения модели (1.1)СОДЕРЖАНИЕ ВВЕДЕНИЕ 2 1. ЛАБОРАТОРНАЯ РАБОТА №1 “РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ (ЛП) С ИСПОЛЬЗОВАНИЕМ Microsoft Excel” 2 1.1. ЦЕЛЬ РАБОТЫ 2 1.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 1.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП [5] 2 1.3.1. ОДНОИНДЕКСНЫЕ ЗАДАЧИ ЛП 2 1.3.1.1. ВВОД ИСХОДНЫХ ДАННЫХ 2 1.3.1.2. Решение задачи 2 1.3.2. ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ 2 1.3.3. ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛП 2 1.3.4. ЗАДАЧИ С БУЛЕВЫМИ ПЕРЕМЕННЫМИ 2 1.3.5. ВОЗМОЖНЫЕ ОШИБКИ ПРИ ВВОДЕ УСЛОВИЙ ЗАДАЧ ЛП 2 1.4. ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 2 1.5. ВАРИАНТЫ 2 2. ЛАБОРАТОРНАЯ РАБОТА №2 (часть I) “ОДНОИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ” 2 2.1. ЦЕЛЬ РАБОТЫ 2 2.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 2.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] 2 2.4. ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 2 2.5. ВАРИАНТЫ 2 3. ЛАБОРАТОРНАЯ РАБОТА №2 (часть II) “АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ ОДНОИНДЕКСНЫХ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ” 2 3.1. ЦЕЛЬ РАБОТЫ 2 3.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 3.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [5,6,7] 2 3.3.1. ЗАДАЧИ АНАЛИЗА ОПТИМАЛЬНОГО РЕШЕНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ 2 3.3.2. ГРАФИЧЕСКИЙ АНАЛИЗ ОПТИМАЛЬНОГО РЕШЕНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ 2 3.3.3. АНАЛИЗ ОПТИМАЛЬНОГО РЕШЕНИЯ НА ЧУВСТВИТЕЛЬНОСТЬ В EXCEL 2 3.3.3.1. Отчет по результатам 2 3.3.3.2. Отчет по устойчивости 2 3.4. ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 2 4. ЛАБОРАТОРНАЯ РАБОТА №3 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. СТАНДАРТНАЯ ТРАНСПОРТНАЯ ЗАДАЧА” 2 4.1. ЦЕЛЬ РАБОТЫ 2 4.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 4.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,2,3,4,6,7] 2 4.3.1. СТАНДАРТНАЯ МОДЕЛЬ ТРАНСПОРТНОЙ ЗАДАЧИ (ТЗ) 2 4.3.2. ПРИМЕР ПОСТРОЕНИЯ МОДЕЛИ ТЗ 2 4.4. ВАРИАНТЫ 2 4.6. ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 2 5. ЛАБОРАТОРНАЯ РАБОТА №4 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. ЗАДАЧА О НАЗНАЧЕНИЯХ” 2 5.1. ЦЕЛЬ РАБОТЫ 2 5.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 5.3. ЗАДАЧА О НАЗНАЧЕНИЯХ. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ [1,3,6,7] 2 5.4. ПОСТАНОВКА ЗАДАЧИ О НАЗНАЧЕНИЯХ 2 5.5. РЕКОМЕНДАЦИИ К РЕШЕНИЮ ЗАДАЧИ О НАЗНАЧЕНИЯХ В ЛАБОРАТОРНОЙ РАБОТЕ №4 2 5.4. ВАРИАНТЫ 2 5.5. ПРИМЕРНЫЕ ВОПРОСЫ ДЛЯ ЗАЩИТЫ РАБОТЫ 2 6. ЛАБОРАТОРНАЯ РАБОТА №5 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ. “ОРГАНИЗАЦИЯ ОПТИМАЛЬНОЙ СИСТЕМЫ СНАБЖЕНИЯ” 2 6.1. ЦЕЛЬ РАБОТЫ 2 6.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 6.3. ПОСТАНОВКА ЗАДАЧИ 2 6.4. РЕКОМЕНДАЦИИ К РЕШЕНИЮ 2 6.5. ВАРИАНТЫ 2 6.6. ЗАЩИТА РАБОТЫ 2 7. ЛАБОРАТОРНАЯ РАБОТА №6 “ДВУХИНДЕКСНЫЕ ЗАДАЧИ ЛП. ОПТИМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ” 2 7.1. ЦЕЛЬ РАБОТЫ 2 7.2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 2 7.3. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ 2 7.4. ПОСТАНОВКА ЗАДАЧИ РАСПРЕДЕЛЕНИЯ ПРОИЗВОДСТВЕННЫХ МОЩНОСТЕЙ 2 7.5. ПОСТРОЕНИЕ И РЕШЕНИЕ РЗ ЛП 2 7.4. ВАРИАНТЫ 2 7.6. ПРИМЕРНЫЕ ВОПРОСЫ НА ЗАЩИТЕ РАБОТЫ 2 ЛИТЕРАТУРА 2 ВВЕДЕНИЕ В данном учебно-методическом пособии рассмотрены основные типы задач линейного программирования, даны рекомендации по построению их математических моделей и поиску оптимальных решений средствами табличного редактора Microsoft Excel. В целях более эффективного усвоения учебного материала пособие построено по принципу лабораторных работ, разбитых по типам задач линейного программирования. В рамках лабораторной работы №1 представлены: · подробные методики и конкретные примеры решения одноиндексных и двухиндексных задач линейного программирования с различными видами ограничений; · возможные ошибки при вводе условий задач линейного программирования в MS Excel. Лабораторные работы № 2–7 содержат: · теоретическое описание математических моделей задач линейного программирования определенного типа и методики их построения; · примеры решения конкретных задач описанного типа или рекомендации к их решению. Каждая лабораторная работа включает в себя 12 вариантов учебных задач определенного типа, а также список примерных вопросов для защиты работы, охватывающих как теоретические положения, так и конкретные варианты заданий. Выбранный способ изложения учебного материала позволяет использовать данное пособие как в учебных целях, так и для решения практических задач с использованием Microsoft Excel.
СПИСОК ИСПОЛЬЗУЕМЫХ ОБОЗНАЧЕНИЙ 1) ЛП – линейное программирование. 2) ЦФ – целевая функция. 3) РЗ – распределительная задача. 4) ТЗ – транспортная задача. 5) * – вопрос повышенной сложности.
1. ЛАБОРАТОРНАЯ РАБОТА №1 “РЕШЕНИЕ ЗАДАЧ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ С ИСПОЛЬЗОВАНИЕМ Microsoft Excel” ЦЕЛЬ РАБОТЫ Приобретение навыков решения задач линейного программирования (ЛП) в табличном редакторе Microsoft Excel. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ Для модели ЛП, соответствующей номеру Вашего варианта, найдите оптимальное решение в табличном редакторе Microsoft Excel и продемонстрируйте его преподавателю. 1.3. ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ Microsoft Excel ДЛЯ РЕШЕНИЯ ЗАДАЧ ЛП [5] Для того чтобы решить задачу ЛП в табличном редакторе Microsoft Excel, необходимо выполнить следующие действия. 1. Ввести условие задачи: a) создать экранную форму для ввода условия задачи: · переменных, · целевой функции (ЦФ), · ограничений, · граничных условий; b) ввести исходные данные в экранную форму: · коэффициенты ЦФ, · коэффициенты при переменных в ограничениях, · правые части ограничений; c) ввести зависимости из математической модели в экранную форму: · формулу для расчета ЦФ, · формулы для расчета значений левых частей ограничений; d) задать ЦФ (в окне "Поиск решения"): · целевую ячейку, · направление оптимизации ЦФ; e) ввести ограничения и граничные условия (в окне "Поиск решения"): · ячейки со значениями переменных, · граничные условия для допустимых значений переменных, · соотношениямежду правыми и левыми частями ограничений. 2. Решить задачу: a) установить параметры решения задачи (в окне "Поиск решения"); b) запустить задачу на решение (в окне "Поиск решения"); c) выбрать формат вывода решения (в окне "Результаты поиска решения"). Одноиндексные задачи ЛП Рассмотрим пример нахождения решения для следующей одноиндексной задачи ЛП:
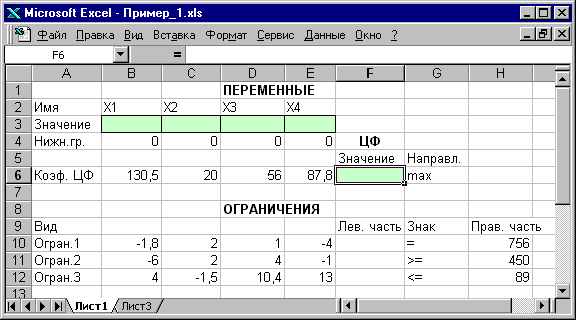
Ввод исходных данных Создание экранной формы и ввод в нее условия задачи Экранная форма для ввода условий задачи (1.1) вместе с введенными в нее исходными данными представлена на рис.1.1.
Рис.1.1. Экранная форма задачи (1.1) (курсор в ячейке F6) В экранной форме на рис.1.1 каждой переменной и каждому коэффициенту задачи поставлена в соответствие конкретная ячейка в Excel. Имя ячейки состоит из буквы, обозначающей столбец, и цифры, обозначающей строку, на пересечении которых находится объект задачи ЛП. Так, например, переменным задачи (1.1) соответствуют ячейки B3 ( Ввод зависимостей из математической модели в экранную форму Зависимость для ЦФ В ячейку F6, в которой будет отображаться значение ЦФ, необходимо ввести формулу, по которой это значение будет рассчитано. Согласно (1.1) значение ЦФ определяется выражением
Используя обозначения соответствующих ячеек в Excel (см. рис.1.1), формулу для расчета ЦФ (1.2) можно записать как сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов ЦФ (B6, C6, D6, E6), то есть
Чтобы задать формулу (1.3) необходимо в ячейку F6 ввести следующее выражение и нажать клавишу "Enter"
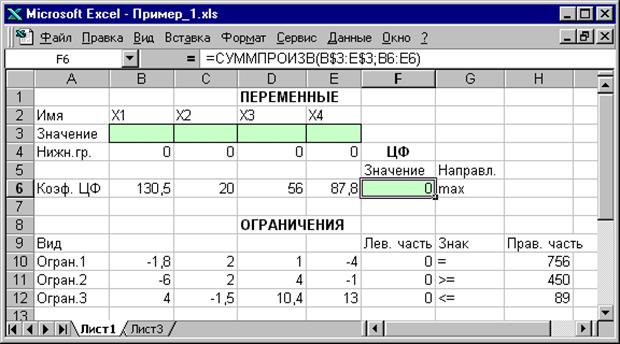
где символ $ перед номером строки 3 означает, что при копировании этой формулы в другие места листа Excel номер строки 3 не изменится; символ : означает, что в формуле будут использованы все ячейки, расположенные между ячейками, указанными слева и справа от двоеточия (например, запись B6:E6 указывает на ячейки B6, C6, D6 и E6). После этого в целевой ячейке появится 0 (нулевое значение) (рис.1.2).
Рис.1.2. Экранная форма задачи (1.1) после ввода всех необходимых формул (курсор в ячейке F6) Примечание 1.1. Существует другой способ задания функций в Excel с помощью режима "Вставка функций", который можно вызвать из меню "Вставка" или при нажатии кнопки " · курсор в поле F6; · нажав кнопку " · выберите в окне "Категория"категорию "Математические"; · в окне "Функция"выберитефункциюСУММПРОИЗВ; · в появившемся окне "СУММПРОИЗВ" в строку "Массив 1" введите выражение B$3:E$3, а в строку "Массив 2" – выражение B6:E6(рис.1.3); · после ввода ячеек в строки "Массив 1" и "Массив 2" в окне "СУММПРОИЗВ" появятся числовые значения введенных массивов (см. рис.1.3), а в экранной форме в ячейке F6 появится текущее значение, вычисленное по введенной формуле, то есть 0 (так как в момент ввода формулы значения переменных задачи нулевые).
Рис.1.3. Ввод формулы для расчета ЦФ в окно "Мастер функций" Зависимости для левых частей ограничений Левые части ограничений задачи (1.1) представляют собой сумму произведений каждой из ячеек, отведенных для значений переменных задачи (B3, C3, D3, E3), на соответствующую ячейку, отведенную для коэффициентов конкретного ограничения (B10, C10, D10, E10 –1-е ограничение; B11, C11, D11, E11– 2-е ограничение и B12, C12, D12, E12 –3-е ограничение). Формулы, соответствующие левым частям ограничений, представлены в табл.1.1.
Таблица 1.1 Формулы, описывающие ограничения модели (1.1)
Как видно из табл.1.1, формулы, задающие левые части ограничений задачи (1.1), отличаются друг от друга и от формулы (1.4) в целевой ячейке F6 только номером строки во втором массиве. Этот номер определяется той строкой, в которой ограничение записано в экранной форме. Поэтому для задания зависимостей для левых частей ограничений достаточно скопировать формулу из целевой ячейки в ячейки левых частей ограничений. Для этого необходимо: · поместить курсор в поле целевой ячейки F6 и скопировать в буфер содержимое ячейки F6 (клавишами "Ctrl-Insert"); · помещать курсор поочередно в поля левой части каждого из ограничений, то есть в F10, F11иF12,и вставлять в эти поля содержимое буфера (клавишами "Shift-Insert") (при этом номер ячеек во втором массиве формулы будет меняться на номер той строки, в которую была произведена вставка из буфера); · на экране в полях F10,F11 и F12 появится 0 (нулевое значение) (см. рис.1.2).

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|

 ), C3 (
), C3 (  ), D3 (
), D3 (  ), E3 (
), E3 (  ), коэффициентам ЦФ соответствуют ячейки B6 (
), коэффициентам ЦФ соответствуют ячейки B6 (  130,5), C6 (
130,5), C6 (  20), D6 (
20), D6 (  56), E6 (
56), E6 (  87,8), правым частям ограничений соответствуют ячейки H10 (
87,8), правым частям ограничений соответствуют ячейки H10 (  756), H11 (
756), H11 (  450), H12 (
450), H12 (  89) и т.д.
89) и т.д. .
.
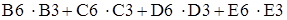 .
.
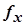 "на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
"на стандартной панели инструментов. Так, например, формулу (1.4) можно задать следующим образом:
 или
или

 или
или
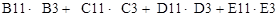
 или
или