Диагностические модели механизма

Рассмотрим вопросы, касающиеся методологии диагностирования эксплуатационных дефектов машин возвратно-поступательного принципа действия, в которых со временем наработки развиваются деградационные процессы, приводящие к неисправностям, нарушению геометрии контактирующих поверхностей, уменьшению эксплуатационной надежности механизмов.

Представим механизм в виде динамической системы со степенями свободы:

[M][X] + [K][X] + [G][X] = [G] (2.1)

где [М], [К], [G] - симметричные n х n матрицы коэффициентов инерции демпфирования, и жёсткости; [х] и [G] - n мерные вектора координат и действующих сил, предполагает, что зависимость акустических характеристик объекта от вида дефекта входит в уравнение в неявном виде. В условиях функционирования возмущающие воздействия и динамические характеристики механизма являются ненаблюдаемыми параметрами, а вид и глубина развития дефекта определяется только по выходным реакциям в местах установки датчиков.

Рассмотрим несколько конкретных примеров. Дефект типа неуравновешенности ротора влияет на функцию возбуждения g(t,r), повышая амплитуду воздействия на частоте вращения ротора, что вызывает увеличение амплитуды отклика механической системы на той же частоте. В зоне низких частот, когда механизм колеблется как единое целое, его поведение можно описать одним уравнением:

(mx)״+ (kx)׳ cx = g (t) (2.2)

Связь между амплитудой действующей силы и реакцией механизма на частоте возбуждения описывается амплитудно - частотной характеристикой

обычного гармонического осциллятора, функция передачи которого имеет вид:

H (jω) = ω²_c / (1 - (ω/ω_c)² + j (ω/ω_c) 1/Q) (2.3)

Где ω_c = √c/m собственная частота, Q =√ cm/k добротность осциллятора

Структурную схему диагностической модели в этом случае можно представить в виде двухполюсника, изображенного на рис. 2.2.

Рис. 2.2 Структурная схема одномерной диагностической модели

Если исходить из данной диагностической модели, то результат диагностирования значения дисбаланса не должен зависеть от места установки датчика. Амплитуда отклика на частоте вращения ωвр определяется значением эксцентриситета в соответствии с формулой:

X (w_BP) = ω² / {[k / (ω²m)] ^-1} (2.4)

Для постановки диагноза достаточно оценить отклонение амплитуды колебаний от нормы на частоте воздействия дефекта. Этой же моделью можно воспользоваться при диагностировании дефектов изготовления и монтажа механизмов, проявляющихся в низкочастотном диапазоне.

При одновременном воздействии нескольких дефектов, проявляющихся на различных частотах, диагностическая модель механизма принимает вид, изображенный на рис. 2.3

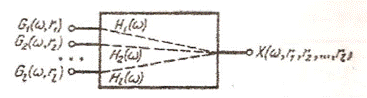
Рис. 2.3 Обобщенная структурная схема многомерной диагностической модели механизма

При одновременном воздействии нескольких дефектов, вызывающих изменение амплитуды колебаний механизма на одной и той же частоте, данная модель непригодна. Такая картина может наблюдаться при отклонении от соосности валов, неравномерности изнашивания за оборот колеса, поломки зуба и ряда других причин. Для того чтобы различить дефекты, вызывающие коррелированные воздействия на механизм, следует изменить диагностическую модель, обратившись не к анализу непосредственных проявлений дефектов на определенной частоте колебаний, а к сопутствующим явлениям, проявляющимся в других частотных диапазонах, причем не обязательно сказывающихся на энергетических характеристиках виброакустического сигнала. Диагностический признак при этом более информативен, если его размерность >1.

В среднечастотном диапазоне от 200-500 Гц до 1- 2 кГц, когда колебания механизма можно описать системой дифференциальных уравнений, диагностическая модель приобретает вид, изображенный на рис.2.4

[M][X] + [K][X] + [C][X] = [G] (2.5)

Рис. 2.4 Структурная схема линейной многомерной системы с р входами и n выходами.

При некоррелированных воздействиях дефектов и установке датчиков в непосредственной близости от источника возбуждения диагностическая модель упрощается (рис. 2.5).

Рис. 2.5 Структурная схема многомерной диагностической модели с L некоррелированными входами и L некоррелированными выходами

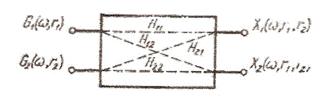
При коррелированных воздействиях дефектов диагностическая модель приобретает вид, изображенный на рис. 2.6

Рис. 2.6 Структурная схема двухмерной модели при коррелированных воздействиях

Выход из этой ситуации тот же, что и в низкочастотной области. Поиск характерных диагностических признаков для того, чтобы привести модель к виду, изображённому на рис 2.6. Есть ещё один выход - анализ акустических процессов в высокочастотной области от 20 кГц. Обращение к методам демодуляции вынужденных и собственных колебаний узлов механизма (или измерительной механической системы) дает возможность сформировать характерные диагностические признаки и воспользоваться упрощенными диагностическими моделями, типа изображенных на рис. 2.3 и 2.4.

Одним из способов оценки изменения оператора динамического звена является снятие амплитудно-частотной характеристики (АЧХ) методом синхронного следящего анализа виброакустических процессов при плавном подъеме или спуске оборотов механизма. Это дает возможность оценки изменения структурных параметров по изменению амплитуд и изменению собственных частот механизма.

В тех случаях, когда дефект переводит механическую систему из класса линейных в нелинейных, рассмотренные выше динамические модели малоэффективны. Поскольку диагностирование функционирующих механизмов осуществляется только по выходным параметрам (характеристикам виброакустического сигнала), то важно отдавать себе отчет в том, что любая динамическая модель механизма является приближенной: ее можно использовать лишь для качественного описания связи вектора дефектов R с вектором диагностических признаков U, особенно в области частот выше 1-2 кГц, когда механизм нужно рассматривать как систему с распределенными параметрами.

Не нашли, что искали? Воспользуйтесь поиском по сайту: