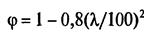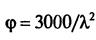|
|
УКАЗАНИЯ К ВЫПОЛНЕНИЮ ЗАДАЧИ 21) Выполнить эскиз соединения 2) Найти допускаемое усилие Fдоп = 2 Ауг Rу γс= ,кн 3) Назначить катет шва кf = t – (1÷3), мм (кмин = 4 мм ) 4) Найти допускаемое усилие на шов пера Fдоппера= Fдоп * z0 / b , кн 5) Найти допускаемое усилие на шов обушка Fдопоб= Fдоп *(b - z0) / b , кн 6) Определить длину шва пера Lwпера≥ Fдоппера / (2 * 0,7кf Rwf γс) = , см 7) Определить необходимую длину шва обушка Lwоб≥ Fдопоб / (2 * 0,7кf Rwf γс) = , см Длина шва не должна превышать 60 кf Lфл ≤ 60кf и не должна быть меньше 40 мм Ответ: Lwпера =… см ; Lwоб = … см
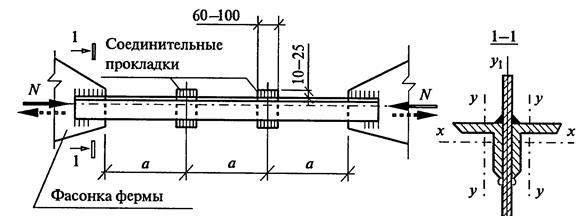
Задача 3. Проверить прочность соединения фланговыми швами элемента из двух равнополочных уголков b x t , мм к фасонке толщиной tф (рисунок 2). Расчётное усилие N. Материал листов и фасонки – сталь С235. Расчётное сопротивление стали по пределу текучести Ry = 23 кн/см2. Сварка п/автоматическая. Расчётное сопротивление металла шва при срезе Rwf = 18 кн/см2 Коэффициент βf =0,85
Алгоритм решения 1. Проверить прочность основного сечения уголков (Найти напряжения и сравнить с расчетным сопротивлением) 2. Определить действующую нагрузку на шов пера 3. Определить действующую нагрузку на шов обушка 4. Назначить катеты швов пера и обушка 5. Проверить прочность соединений. Определить напряжения в сечении швов и сравнить с расчетным сопротивлением 6. Сделать вывод 4. КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:
1. Как определяется конструктивный катет шва? 2. Какими размерами ограничивается длина флангового шва? 3. Чем определяется катет шва у пера уголка? 4. Что такое равнопрочность?
Литература: В.И. Сетков «Строительные конструкции»,М., ИНФРА-М,2009, с. 228 – 233, 287 – 292
ПРАКТИЧЕСКАЯ РАБОТА № 13
Тема: Расчет стержней фермы. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Для стальных ферм наиболее распространенными являются сечения стержней из двух спаренных уголков ( как равнополочных, так и неравновнополочных) . В качестве геометрической длины стержней принимается расстояние между центрами узлов. При расчете устойчивости стержней устанавливается их расчетная длина lef, которая учитывает характер возможного изгиба стержней и конструктивные особенности прикрепления стержней в узлах. Расчетные длины принимаются в соответствии с требованиями табл.11 СНиП
Сжатые стержни рассчитываются как центрально-сжатые элементы для которых должна обеспечиваться прочность, устойчивость и ограничивается гибкость. Требуемая площадь сечения стержня фермы определяется по формуле: К деревянным фермам построечного изготовления относятся фермы, элементы которых выполнены из цельных не клееных бревен, брусьев или досок с узловыми соединениями на нагелях (болтах, гвоздях) или на лобовых врубках. Растянутые элементы решетки и нижний пояс фермы часто делается стальными. По очертанию фермы построечного изготовления могут быть треугольными и многоугольными. Ширина сечения элементов фермы определяется по предельному значению гибкости. Для элементов ферм установлены следующие предельные значения гибкостей (λпр): - для верхнего пояса λпр=120 ; - для элементов решетки λпр=150 ; - для нижнего пояса из стали λпр=400. Ширину сечения верхнего пояса и элементов решетки целесообразно назначать по значению радиуса инерции.
После подбора сечений элементов фермы, выполняют проверку их прочности.
ЗАДАНИЯ ПО ВАРИАНТАМ Задача 1 . Подобрать сечение сжатого стержня решетки стальной фермы при действии сжимающей нагрузки N. Предельная гибкость λмакс= 210 - 60α . Толщина фасонки tф = 12 мм.
Ход решения. 1. Находим расчетное сопротивление стали Ry ( таблица 1 Приложение 1) 2. Определяем коэффициент условия работы, предполагая, что гибкость стержня будет больше 60. (таблица 4 Приложение 3 ) γc = 0,8 3. Определяем расчетные длины стержня по табл.11 СНиП: (таблица 5 Приложение3) в плоскости фермы lef x= 0,8 l =… см из плоскости фермы lef y= l =… см 4. Принимаем предварительно гибкость λ = 100 и находим коэффициент продольного изгиба φ ( таблица 1 Приложение 3) 5. Находим требуемую площадь сечения стержня
6. Определяем требуемые радиусы инерции: ix =lef x /λ = см iy = lef y /λ = см 7. По сортаменту ( таблица 3 Приложение 2) подбираем уголки по трем параметрам: А, ix , iy ; при подборе уголков не забываем , что площадь стержня состоит из двух уголков и требуемая площадь сечения одного уголка Ауг= А / 2 . Принимаем уголок … х … с площадью Атаблуг = …. см2 больше `требуемой. Выписываем из сортамента ix табл = … см; iyтабл =… см. 8. Проверяем принятое сечение: · определяем гибкости λх = lef x / ix табл λу= lef y / iyтабл · по наибольшей гибкости определяем коэффициент продольного изгиба φ2 = … ( таблица 1 Приложение 3 ) · находим значение коэффициента α = N / (φ2 *2Aтаблуг * Ry* γc) т.к значение коэффициента получилось больше 0,5 принимаем величину коэффициента α = … (если коэффициент получается меньше 0,5 то α = 0,5 ) · определяем предельную гибкость λмакс = 210 - 60α = … Наибольшая гибкость стержня меньше предельной, следовательно, гибкость стержня в пределах нормы. ( таблица 6 Приложение 3) ( Если нет, то необходимо принять другой размер уголка) · Проверяем устойчивость σ = N / (φ2 *2Aтаблуг ) = … ≤ Ry*γc ,кН/см2 Вывод: Устойчивость обеспечена, принимаем сечение стержня из двух уголков размером … х … . Задача 2. Подобрать сечение сжатого стержня решетки деревянной фермы при действии статической нагрузки N
1. Находим расчетное сопротивление древесины Rc с учетом переходного коэффициента mn ( СНиП II-25-80) таблицы 2,3 Приложение 1 2. Определяем расчетную длину стержня в плоскости фермы lef,x lef,x =0,8 l 3. Находим требуемую площадь сечения стержня, для этого предварительно принимаем гибкость стержня λ= 100 и по гибкости находим коэффициент продольного изгиба φ=0,434 А = N / φ Rc γc , см2 4. Находим минимальный радиус инерции по предельному значению гибкости. - для верхнего пояса λпр=120 ; - для элементов решетки λпр=150 ; i = lef.x / λпр , см 5. Находим ширину сечения по значению радиуса инерции. bmin = i / 0,29
6. Ориентировочно определяем высоту сечения h = A / bmin 7. По сортаменту ( таблица 5 Приложение 2) назначаем размеры сечения стержня и определяем окончательную площадь сечения А2 8. Проверяем сечение на устойчивость: · Находим момент инерции I = b h3 /12 · Радиус инерции i2 = √ I / A2 · Гибкость λ2 = lef.x / i2 · Фактический коэффициент продольного изгиба φ2 = … если λ2 < 70 если λ2 ≥ 70 · Проверяем устойчивость σ = N / A 2 φ2 ≤ Rс γс, кН/см2
Вывод: Устойчивость обеспечена, принимаем сечение стержня деревянной фермы размером … х … .
Контрольные вопросы
1. От чего зависит гибкость стержня фермы? 2. Какие виды деформаций испытывают стержни решетки фермы? 3. Как обеспечивается устойчивость сжатого стержня фермы?
Литература: В.И. Сетков «Строительные конструкции»,М., ИНФРА-М,2009, с. 332 – 335, 342 – 345 ПРАКТИЧЕСКАЯ РАБОТА № 14
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
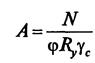
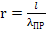, где l – расчетная длина стержня фермы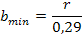
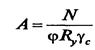см2
