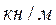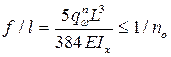|
|
РАСЧЕТНО ГРАФИЧЕСКАЯ РАБОТА №6Тема: Расчет стальных и деревянных центрально-растянутых элементов ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Разрушение растянутых элементов происходит по сечению с наименьшей площадью (Аn) В случае, если ослабление отсутствует, площадь нетто - Аn равна площади брутто А. Расчет прочности ведется по формуле
Длинные растянутые элементы могут изменять свою первоначальную форму в результате чрезмерной гибкости, что может затруднять их применение. Поэтому гибкость ограничивают нормами, проверяя элемент на устойчивость
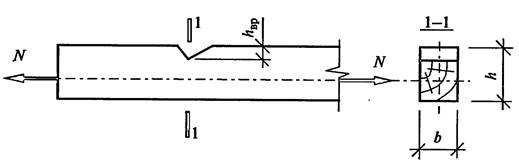
ЗАДАНИЯ Задача 1 Подобрать сечение центрально-растянутого нижнего пояса деревянной фермы. Материал: брус, Сосна, сорт 2-ой. Ослабление за счет врезки глубиной hвр ( коэффициент условия работы mo = 0,8). На нижний пояс действует растягивающая сила N = ..γn= 0,95. Расчетная длина lo = …метров. Предельная гибкость растянутых поясов в вертикальной плоскости λmax = 150
Алгоритм решения задачи : 1. Определяем расчетное сопротивление растяжению вдоль волокон Rp (таблица 2 Приложение 1) 2. Находим усилие с учетом коэффициента надежности по ответственности Nр = N γn , кн 3. С учетом коэффициента условия работы определяем требуемую площадь сечения нетто Fнттреб= Nр/Rpmo , см2 mo = 0,8 – с ослаблением в расчетном сечении 4. Задаемся толщиной пояса b = …см (4,0; 4,4; 5,0; 6,0; 7,5 см) 5. Определяем требуемую площадь ослабления Fослтреб= b hвр , см2 6. Определяем требуемую площадь сечения Fтреб = Fнттреб + Fослтреб 7. По требуемой площади подбираем сечение пояса, руководствуясь сортаментом (таблица 5 Приложение 2) 8. Определяем фактическое значение площадей : Fбр = b h ,см2 Fнт = b (h – hвр) , см2 9. Выполняем проверку прочности σ = Np/ Fнт ≤ Rp mo 10. Выполняем проверку гибкости
где r – радиус инерции сечения r = 0,289 b ,см
Вывод: прочность и жесткость сечения с размерами … х … обеспечена.
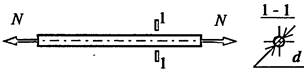
Задача 2 Проверить прочность и гибкость стального центрально-растянутого стержня круглого сечения диаметром d =… мм. Сталь С245 Растягивающая сила N = .. кн Коэффициент надежности по назначению γn= 0,95 Коэффициент условия работы γс= 0,9 . Расчетная длина стержня lef = … Предельная гибкость λпред = 400.
Алгоритм решения задачи : 1. Определяем расчетное сопротивление растяжению Rу , кн/см2
(таблица 1 Приложение 1)
2. Находим усилие с учетом коэффициента надежности по ответственности Nр = N γn , кн 3. Находим площадь сечения круглого стержня А , см2 4. Проверяем прочность стержня
5. Определяем радиус инерции затяжки i = 0,25d , см 6. Проверяем гибкость стержня λ = lef / i ≤ λпред
Вывод: прочность и гибкость стержня обеспечены (или не обеспечены, если условия не удовлетворяются) 4. КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:
1. Чем отличается площадь поперечного сечения «нетто» от площади поперечного сечения «брутто»? 2. Нужно ли суммировать ослабления растянутых элементов, если они находятся на расстоянии не более 200 мм друг от друга? 3. Какие материалы используются для конструкций растянутых элементов? 4. Какие факторы влияют на прочность растянутого элемента?
Литература: В.И. Сетков «Строительные конструкции»,М., ИНФРА-М,2009, с. 164- 169
РАСЧЕТНО ГРАФИЧЕСКАЯ РАБОТА № 7
Тема: Расчет стальной балки. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ Рациональными сечениями при изгибе являются те, которые обладают большим сопротивлением изгибу при прочих равных условиях. Например, прямоугольное сечение с одной и той же площадью и размерами будет более рациональным, если его расположить длинной стороной по вертикали
Также рациональными сечениями являются симметричные сечения с развитой вертикальной стенкой: двутавровые прокатные балки, балки «Н»-образного составного сечения. Рассчитать на прочность – это значит определить напряжения и сравнить его с расчетным сопротивлением или допускаемым напряжением. σимах = Ммах / Wx = … ≤ Ry, кН/см2 По этому неравенству проводят проверочные расчеты после окончания конструирования балки. При проектировочном расчете определяются требуемые размеры поперечных сечений балки или № прокатной балки
ЗАДАНИЯ Задача 1 Подобрать необходимый № двутавровой балки при действии равномерно распределенной нагрузки (q ) на балку настила пролетом (L) и проверить её на прочность. Материал балки: сталь С245 с расчетным сопротивлением Ry = 24 кн/см2. Нормативный прогиб равен (1/200)L. Коэффициент надежности по нагрузке для стальных балок γf =1,05
3. Алгоритм решения задачи : 1. Определяем расчетную нагрузку q = qn γf , кН /m 2. Находим максимальный изгибающий момент Ммах = q L2 / 8 ,кН х м 3. Требуемый момент сопротивления сечения Wx тр = Ммах / Ry γс , см3 4. По сортаменту (таблица 1 Приложение 2) подбираем необходимый № профиля из условия, что фактический момент сопротивления сечения Wx ≥ Wx тр. Выписываем геометрические характеристики (Wx) и массу одного погонного метра (G) 5. Находим фактическую нагрузку с учетом собственного веса балки qф = q + G γf , кН/м 6. Находим фактический изгибающий момент Мфакт = qф L2 / 8 , кН х м 7. Проверяем прочность сечения σимах = Мфакт / Wx = … ≤ Ry γс, кН/см2 8. Определяем прогиб балки
Е = 2,1 * 104 кн/см2 – модуль упругости стали qn= qф / γf γf= 1,05 – коэффициент надежности по нагрузке Ix - момент инерции сечения ( по сортаменту) , см4 9. Проверяем жесткость балки f ≤ fn fn = L/200 см 10.Сделать выводы. ( Балка №… обеспечивает необходимую прочность и жесткость.)
Задача 2 Сконструировать сварную балку «Н»-образного сечения пролетом (L) при действии равномерно распределенной нагрузки (q ) и проверить её на прочность. Материал балки: сталь С235 с расчетным сопротивлением Ry = 23 кн/см2. Нормативный прогиб равен 1/400. Коэффициент надежности по нагрузке для стальных балок γf =1,05
1. Определяем расчетную нагрузку q = qn γf , кН /м
2. Изгибающий момент, действующий посередине пролёта главной балки: Ммах = q L2 / 8 ,кн м 3. Требуемый момент сопротивления сечения главной балки:
т.к.
4. Минимальная высота балки:
1/no - нормативный прогиб = 1/400
5. Ориентировочная толщина стенки балки:
6. Оптимальная высота стенки:
к – коэффициент, зависящий от конструктивного оформления 7. Назначаем высоту стенки балки, руководствуясь данными
8. Минимальная требуемая толщина стенки
для стали СтЗ: gm = 1,025 - из условия обеспечения местной устойчивости: для низколегированных сталей 9. Окончательно назначаем толщину стенки: 10. Назначаем толщину пояса балки в пределах 12 - 40 мм из 11. Высота балки :
12. Требуемая площадь сечения пояса
13. Требуемая ширина пояса: 14. Окончательно назначаем ширину пояса
15. Местная устойчивость пояса обеспечена, если
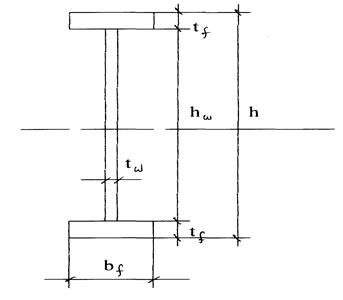
16. Проверка сварной балки на прочность и жесткость 16.1. Геометрические характеристики сечения: - площадь - статический момент полусечения относительно нейтральной оси Х:
- момент инерции сечения:
- момент сопротивления сечения:
16.2. Собственный вес 1 п.м. балки:
где 16.3. Изгибающий момент от собственного веса балки:
16.4. Суммарный изгибающий момент:
16.5. Суммарная поперечная сила равна опорной реакции
RA=q L/2 16.6. Проверка прочности по нормальным напряжениям:
по касательным напряжениям:
16.7.Нормативная нагрузка с учетом собственного веса балки: qn∑ = qn + qnbp , 16.8. Проверка жесткости:
Вывод:Прочность и жесткость главной балки подобранного сечения обеспечена.
4. КОНТРОЛЬНЫЕ ВОПРОСЫ ДЛЯ САМОПРОВЕРКИ:
1. Назовите типы сечений стальных балок? 2. Какие существуют виды расчетов стальных балок? 3. Как обеспечивается устойчивость балки?
Литература: В.И. Сетков «Строительные конструкции»,М., ИНФРА-М,2009, с. 181- 191 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
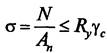
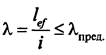
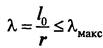
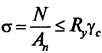
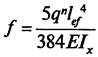
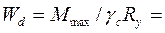 , см3
, см3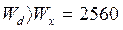 см3 , то балку проектируем составной.
см3 , то балку проектируем составной.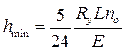 , см
, см ,мм
,мм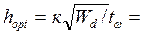 , см
, см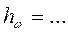 , см
, см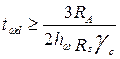 ,см
,см 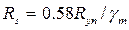 , кн/см
, кн/см - нормативное сопротивление по пределу текучести (таблица 1 Прил.1)
- нормативное сопротивление по пределу текучести (таблица 1 Прил.1)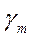 - коэффициент надежности по материалу
- коэффициент надежности по материалу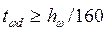 ,см
,см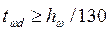 ,см
,см = ... , мм в пределах 8¸16 мм
= ... , мм в пределах 8¸16 мм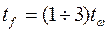 , соблюдая сортамент (таблица 4 Приложение 2)
, соблюдая сортамент (таблица 4 Приложение 2)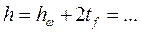 ,см
,см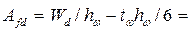 , см2
, см2 , см
, см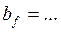 ,см из условия
,см из условия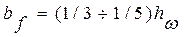 , см и сортамента на широкополосную сталь
, см и сортамента на широкополосную сталь
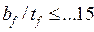
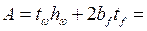 , см2
, см2 , см3
, см3 , см4
, см4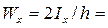 , см3
, см3 ,
, 
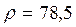
 - удельный вес стали
- удельный вес стали ,
, 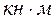
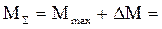 ,
, 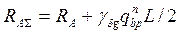 ,
, 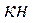
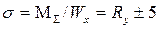 % ,
% , 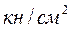
 ,
,