
|
|
Методы выявления основной тенденции в рядах динамики
Существует несколько методов обработки рядов динамики, помогающих выявить основную тенденцию развития явления (тренд). К ним относятся: · метод укрупнения интервалов; · метод скользящей средней;
Во всех методах вместо фактических уровней при обработке ряда рассчитываются иные уровни, в которых тем или иным способом взаимопогашается действие случайных факторов и тем самым уменьшается колеблемость признаков. Метод укрупнения интерваловоснован на укрупнении периодов времени, к которым относятся уровни ряда динамики. Например, ряд ежедневного выпуска продукции заменяется рядом месячного выпуска продукции и т.д. Метод скользящей среднейсостоит в замене абсолютных данных средними арифметическими за определенные периоды. Расчет средних ведется способом скольжения, т.е. постепенным исключением из принятого периода скольжения первого уровня и включением следующего. Аналитическое выравнивание – это набор уравнения прямой или кривой линии, адекватно выражающей общую тенденцию развития динамического ряда. При выборе уравнения функции руководствуются спецификой изучаемого явления, а так же рядом формальных признаков. Например, если для развития явления характерно достаточно стабильные цепные абсолютные приросты, то выбирается уравнение линейного тренда: Если абсолютные цепные приросты с течением времени постепенно сокращаются, то для характеристики тренда применяется полулогарифмическая кривая: Если явление развивается с достаточно стабильными цепными темпами роста, то для характеристики тренда применяется показательная функция: Если примерно постоянны цепные темпы прироста, то используется парабола второго порядка: Из множества разнообразных функций тренда с формально математической точки зрения наилучшей считается та, которая наименее удалена от эмпирических уровней ряда: В случае применения уравнения прямой линии:
Для вычисления параметров тренда (а0 и а1) необходимо решить систему нормальных уравнений:
Для определения параметров тренда в рядах динамики используется способ, упрощающий расчеты - способ отсчета времени от условного начала, который основан на обозначении в ряду динамики показателей времени таким образом, чтобы сумма t равнялась нулю.( В ряду динамики с нечетным числом уровней, например пять, время t обозначается следующим образом:
С четным числом уровней, например шесть, время обозначается как в таблице:
При использовании этого способа, когда
По окончании расчетов целесообразно построить график, на котором следует изобразить исходные данные и теоретические значения уровней ряда ( Для параболы II – го порядка уравнение: yt=a0+a1t+a2t2 если a0 a1 a2
Изучение сезонных колебаний Сезонное колебание – это повторяющиеся устойчивые внутригодовые колебания. Они обусловлены природно-климатическими и другими факторами, определяющими неравномерность производства и потребления во времени. Знание сезонных колебаний позволяет осуществить рациональное внутригодовое и внутримесячное планирование, избежать ненужных потерь и использовать все имеющиеся возможности. В большинстве случаев статистическое исследование рядов динамики за короткие промежутки времени сводятся к изучению сезонных колебаний. Индикатором сезонных колебаний является коэффициент сезонности, который определяется по формуле:
где yi – уровни каждого месяца
Полученные коэффициенты сезонности можно изобразить на графике в виде сезонной волны.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. .
.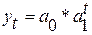 .
. .
. .
. ,
,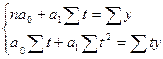
 )
)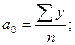
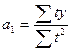
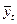 ).
). t = 0
t = 0


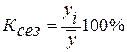
 – среднегодовой уровень, определенный по средней арифметической простой.
– среднегодовой уровень, определенный по средней арифметической простой.