
|
|
Показатели, характеризующие тенденцию динамикиАнализ рядов динамики начинается с определения того, как именно изменяются уровни ряда динамики в абсолютном и относительном выражении. Чтобы проследить за направлением и размером изменений уровней во времени, для рядов динамики рассчитываются следующие показатели: - абсолютные приросты; - темпы роста; - темпы прироста; - абсолютное значение одного процента прироста; - темпы наращивания (изменения); - средний уровень ряда; - средний абсолютный прирост; - средний темп роста; - средний темп прироста В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения . Для расчета показателей динамики на постоянной базе каждый уровень ряда сравнивается с одним и тем же базисным уровнем. Исчисляемые при этом показатели называются базисными . Для расчета показателей динамики на переменной базе каждый последующий уровень ряда сравнивается с предыдущим . Такие показатели называются цепными . 1) Базисный абсолютный прирост определяется как разность между сравниваемым уровнем и уровнем, принятым за постоянную базу сравнения:
2) Цепной абсолютный прирост – разность между сравниваемым уровнем и предшествующим уровнем:
Абсолютный прирост может иметь и отрицательный знак, показывающий, насколько уровень изучаемого периода ниже базисного. Между базисными и абсолютными приростами существует связь: сумма цепных абсолютных приростов равна базисному абсолютному приросту последнего ряда динамики:
Темп роста характеризует отношение двух уровней ряда и может выражаться в виде коэффициента или в процентах. 1) Базисные темпы роста
2) Цепные темпы роста исчисляются делением сравниваемого уровня на предыдущий уровень:
Темпы роста могут выражаться в коэффициентах или в процентах. Выраженные в коэффициентах темпы роста показывают, во сколько раз уровень данного периода больше уровня базы сравнения или какую часть его составляют. При процентном выражении темпы роста показывают, сколько процентов составляет уровень данного периода по сравнению с уровнем базы сравнения. Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста ( в коэффициентах) равно базисному темпу роста , а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста . Темпы прироста характеризуют абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает , на сколько процентов изменился сравниваемый уровень по отношению к уровню , принятому за базу сравнения . 1) Базисный темп прироста вычисляется делением сравниваемого базисного абсолютного прироста на уровень, принятый за постоянную базу сравнения :
2) Цепной темп прироста - это отношение сравниваемого цепного абсолютного прироста к предыдущему уровню:
Между показателями темпа роста и темпа прироста существует взаимосвязь: Тпр= Тр-100
(при выражении темпа роста в процентах). Кпр= Кр-100
(при выражении темпа роста в коэффициентах). Важным статистическим показателем динамики социально – экономических процессов является темп наращивания , который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала . Вычисляются темпы наращивания делением цепных абсолютных приростов на уровень , принятый за постоянную базу сравнения:
Абсолютное значение одного процента прироста (изменения) представляет собой отношение цепного годового (месячного, квартального) абсолютного прироста (изменения) к цепному годовому (месячному, квартальному) темпу прироста и показывает, какая абсолютная величина скрывается за одним процентом прироста; выражается в абсолютных единицах измерения:
Средние характеристики ряда динамики охватывают изменение явления за весь период, к которому относится ряд динамики. К средним характеристикам относятся: средний уровень ряда, средний абсолютный прирост, средний темп роста и средний темп прироста. Средний уровень ряда ( Для интервального ряда с равным интервалом, он определяется по средней арифметической простой, делением суммы уровней ряда на число периодов.
Для интервального ряда с неравным интерваломсредний уровень ряда определяется по формуле средней арифметической взвешенной: Для моментного ряда с равным интервалом средний уровень ряда определяется по формуле средней хронологической Для моментного ряда с неравным интервалом средний уровень ряда можно определить по формуле средней хронологической взвешенной: Средний абсолютный прирост характеризует скорость развития явления во времени. Его можно определить как среднюю величину из цепных абсолютных приростов:
Либо по данным уровней ряда: Средний темп роста дает сводную характеристику интенсивности изменения явления за весь период ряда динамики. Он может быть определен по формуле средней геометрической на основании данных о цепных темпах роста (в коэффициентах):
Либо на основании данных об уровнях ряда:
Средний темп прироста определяется на основании данных о среднем темпе роста как разность:

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 ;
; ;
; ;
; исчисляются делением сравниваемого уровня на уровень , принятый за постоянную базу сравнения:
исчисляются делением сравниваемого уровня на уровень , принятый за постоянную базу сравнения: ;
;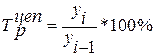
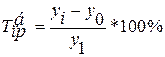
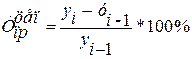
 ;
; ;
; ) показывает, какова средняя величина уровня характерная для всего периода ряда. Средний уровень ряда исчисляется по разному для интервальных и моментных рядов.
) показывает, какова средняя величина уровня характерная для всего периода ряда. Средний уровень ряда исчисляется по разному для интервальных и моментных рядов.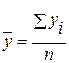 , где
, где  - сумма уровней ряда, n - число периодов
- сумма уровней ряда, n - число периодов , где ti - величина интервала.
, где ti - величина интервала.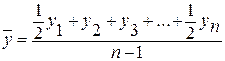 ;
; ;
; , где m - число цепных абсолютных приростов.
, где m - число цепных абсолютных приростов. ;
; , где m - число темпов роста.
, где m - число темпов роста. .
. (в коэффициентах) либо
(в коэффициентах) либо  (в процентах).
(в процентах).