
|
|
Расчет среднестатистической и максимально вероятностиРасчетное прогнозирование полных отказов и показателей Долговечности рельсов Расчет прогнозирования полных отказов и показателей Долговечности рельсов Расчет отказов повреждений рельсов требует расчетов отказов пути при различных условиях эксплуатации. С увеличением наработки существенно возрастает параметр потока отказов, а наработка на отказ уменьшается. Параметр потока
Средняя наработка на отказ
При этом характерна значительная дисперсия (разброс) указанных показателей надежности. Обусловлено это существенной изменчивостью наработки рельсовой стали до усталостного разрушения и изменчивостью параметров жесткости и геометрического состояния пути по его протяжению. Поэтому наработка разных рельсов до отказа является изменчивой величиной, зависящей от множества факторов. Рельсы в главном пути эксплуатируют до установленного показателя - одиночного выхода в дефектные 4-6 шт/км и более в зависимости от класса пути [5]. Потом производят их сплошную замену, а после сортировки и ремонта используют на малодеятельных линиях и станционных путях. Формула отказов рельсов в зависимости от пропущенного тоннажа имеет вид:
Наработка тоннажа определяется по следующей формуле:
Это выражение называется формулой для прогнозных расчетов технического (межремонтного) ресурса железнодорожного пути по допускаемому количеству одиночных отказов рельсов
Ресурс пути в годах между капитальным ремонтом пути t , определяется по формуле:
Формула для определения количества одиночных отказов рельсов за последний год перед их сплошной заменой (капитальным ремонтом пути), определяется по формуле:
На основе имеющихся данных для современных рельсов рекомендуется качестве расчетного значения применить параметр Значения параметра Для незакаленных рельсов Р50, Р65, Р75 в прямых участках пути применительно к среднесетевой совокупности осевых нагрузок (
Эти значения параметра Для термоупрочненных стандартных рельсов и раскисленных по новой технологии современными лигатурами вводится коэффициент Для кривых вводиться коэффициент α
где Итоговые формулы для определения численного значения
Численные значения показателя степени Расчет среднестатистической и максимально вероятности осевых нагрузок
Статистическая совокупность измеренных осевых нагрузок от подвижного состава, тс/ось, представлена в таблице 2.1.
Таблица 2.1 Результаты измерений осевых нагрузок от подвижного состава
Полученные значения случайной величины называются простой статистической совокупностью. Для установления закономерности исследуемой величины и ее характеристики простая статистическая совокупность подвергается обработке: а) Все данные располагаются в порядке возрастания или убывания значений случайной величины. Получается так называемый вариационный ряд. Данные приведенного выше результата измерений, расположенные в порядке возрастания, представлены в таблице 2.2. б) Данные вариационного ряда разбиваются на группы (разряды). Число разрядов зависит от объемов выборки. Практика показывает, что в большинстве случаев целесообразно выбирать число разрядов порядка 10-20. Таблица 2.2 Вариационный ряд осевых нагрузок, измеренных на участке
Величина интервала разряда зависит от размаха колебаний случайной величины и минимальных интервалов. Проще брать разряды одинаковыми по величине интервала. Крайние значения случайной величины при небольшом числе данных обычно объединяются в один – два разряда с увеличенным интервалом.
Величина интервала определяется по формуле:
Например, для вариационного ряда при k =12, в) По вариационному ряду в каждом разряде подсчитывается число наблюдений (частоты), затем определяются значения частостей:
г) Полученные значения разрядов частот и частостей оформляются в виде статистического ряда, который приведен в таблице 2.3.
Таблица 2.3 Статистический ряд случайных величин
Например, частость (
д) Для наглядности статистическое распределение случайной величины изображается гистограммой, которая представляет собой графическое изображение статистического ряда. Соединив середины верхних сторон прямоугольников, получим многоугольник распределения случайной величины (рис.2.1). Из гистограммы рис.2.1 видно, что статистический ряд распределяется неравномерно, но можно установить, что частота е) По данным статистического ряда определяются числовые характеристики простой статистической совокупности: - первый начальный момент или статистическое среднее:
Рисунок 2.1. Гистограмма или многоугольник распределения по данным статистического ряда
где
- статистическая дисперсия:
где
- статистическое среднее квадратическое отклонение:
Расчет описанных выше характеристик произведен в табличной форме и представлен в таблице 2.3. При подстановке полученных результатов:
После выполняют выравнивание статистического ряда и проводится оценка согласования теоретического и статистического распределения. Подбор закона распределения с достаточной точностью описывающего распределение случайной величины производят исходя из физической сущности исследуемого процесса. Дополнительными признаками могут служить внешний вид гистограммы или многоугольника распределения и значения числовых характеристик статистического распределения случайной величины. Так, для нормального распределения все рассеивания (с точностью до 0,1 %) укладываются на участке Для проверки гипотезы о законе распределения измеряемой случайной величины производят расчет координат теоретической кривой распределения и проверку ее согласия со статистическим распределением. Координаты теоретической кривой распределения рассчитываются для граничных значений разрядов статистического ряда по его числовым характеристикам путем нахождения вероятности Для нормального закона распределения измеряемой случайной величины Х вероятность попадания ее в
Частоты теоретического распределения случайной величины определяются как:
где
Все расчеты сведены в таблицу 2.4. Таблица 2.4 Расчет координат теоретического ряда распределения осевых нагрузок
Примечание:
На рисунке 2.2 представлена гистограмма или многоугольник распределения по данным теоретического ряда таблицы 2.4. Многоугольник распределения имеет форму симметричного «колокола» (частость постепенно увеличивается до середины и потом плавно уменьшается), что свидетельствует о правильности ряда для нормального закона распределения. Вопрос согласования теоретического и статистического распределения решается с помощью «критериев согласия».
Рисунок 2.2. Гистограмма и многоугольник распределения по данным теоретического ряда
Наиболее распространенным в практике измерений является критерий Пирсона. При проверке согласованности теоретического и статистического распределения по критерию Пирсона выполняются следующие операции: а) Подсчитывается величина
где
Частоты теоретического распределения случайной величины
где
б) Определяется число степеней свободы
Для нормального распределения:
в) Для значения Для данного примера Правило Романовского значительно облегчает применение согласия Пирсона для оценки расхождения между теоретическим и статистическим распределением. Согласно этому правилу, если
то согласование теоретического и статистического распределений можно считать хорошим. В нашем случае имеем: Максимальная вероятная осевая нагрузка
По формуле 2.3 определяются для прямых и кривых участков отказы рельсов в зависимости от пропущенного тоннажа (принимаем шаг наработки 50 млн.т брутто) до величины допускаемого количества отказов рельсов [h]. Результаты расчетов по определению отказов рельсов сводятся в таблицу, и строится график зависимости отказов рельсов от пропущенного тоннажа. Наработка тоннажа, при которой количество отказов рельсов будет превышать допускаемому, прогнозный ресурс в годах между капитальными ремонтами пути и количества одиночных отказов рельсов за последний год перед капитальным ремонтом пути определяются по формулам 2.4, 2.6 и 2.7 соответственно.

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 определяется по формуле:
определяется по формуле: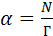 (2.1)
(2.1)
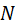
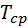 определяется по формуле:
определяется по формуле: (2.2)
(2.2)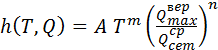 (2.3)
(2.3)


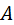 ,
,  ,
, 
 (2.4)
(2.4)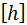 в среднем по рассматриваемому участку
в среднем по рассматриваемому участку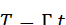 (2.5)
(2.5) (2.6)
(2.6) (2.7)
(2.7)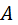 Р50 = 4·10-5,
Р50 = 4·10-5,  , равный соответственно 1,5 и 1,25, а при термоупрочнении и новой технологии раскисления – 1,75.
, равный соответственно 1,5 и 1,25, а при термоупрочнении и новой технологии раскисления – 1,75. (2.8)
(2.8)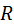 – радиус кривой, м.
– радиус кривой, м. (2.9)
(2.9) (2.10)
(2.10)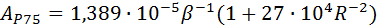 (2.11)
(2.11)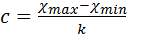 (2.12)
(2.12)


 в вариационном ряду.
в вариационном ряду.
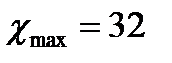 ;
; 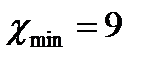
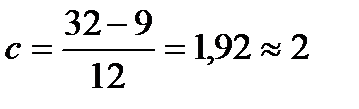
 (2.13)
(2.13)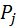
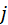 -ом разряде;
-ом разряде;
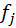
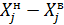



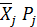

 ) для первого разряда статистического ряда (таблица 2.3) будет равна
) для первого разряда статистического ряда (таблица 2.3) будет равна 
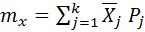 (2.14)
(2.14)
 - среднее значение промежутка определяется по формуле:
- среднее значение промежутка определяется по формуле: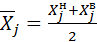 (2.15)
(2.15) (2.16)
(2.16)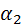 - статистический второй начальный момент, который определяется по формуле:
- статистический второй начальный момент, который определяется по формуле: (2.17)
(2.17) (2.18)
(2.18) тс,
тс, 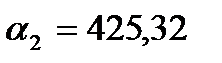
 т/с2
т/с2 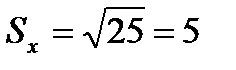 т/с
т/с .Для рассматриваемой статистической совокупности гистограмма или многоугольник распределения имеют вид, приведенный на рисунке 2.1. По их внешнему виду можно предположить, что осевые нагрузки можно описать нормальным законом распределения.
.Для рассматриваемой статистической совокупности гистограмма или многоугольник распределения имеют вид, приведенный на рисунке 2.1. По их внешнему виду можно предположить, что осевые нагрузки можно описать нормальным законом распределения. попадания измеряемой величины в определенный интервал.
попадания измеряемой величины в определенный интервал.
 (2.19)
(2.19)
 в
в 

 (2.20)
(2.20)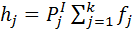 (2.21)
(2.21) - частость распределения в j-том разряде;
- частость распределения в j-том разряде;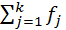 - общее число измерений, принятых к исследованию.
- общее число измерений, принятых к исследованию.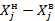


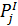



 по формуле:
по формуле: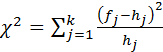 (2.22)
(2.22)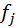 и
и  – частоты соответственно статистического и теоретического распределения в
– частоты соответственно статистического и теоретического распределения в  могут быть определены по формуле:
могут быть определены по формуле: (2.23)
(2.23)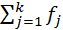 - общее число измерений;
- общее число измерений;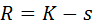 (2.25)
(2.25)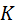


 так, что отклонения между теоретическим и статистическим распределением вызваны случайным колебанием измеряемой величины в выборке.
так, что отклонения между теоретическим и статистическим распределением вызваны случайным колебанием измеряемой величины в выборке.  ,. R=12–3=9. Из таблицы приложения III определяем
,. R=12–3=9. Из таблицы приложения III определяем  = 0,97, что соответствует хорошей сходимости теоретического и статистического распределений.
= 0,97, что соответствует хорошей сходимости теоретического и статистического распределений.
 . Это свидетельствует о хорошей сходимости теоретического и статического распределения.
. Это свидетельствует о хорошей сходимости теоретического и статического распределения. (2.26)
(2.26)