
|
|
Из которой этот знаменатель вычеркнут.Таким образом,
Поместим A, B, C не в числителях, а перед дробями:
Значит, Все интегралы – простейшие и находятся по таблице, поэтому
Ответ:а) б) Пример 2. Пусть для дроби
Корни знаменателей:
Итак,
По таблице основных интегралов находим, что
Ответ: а) б) Пример 3. Пусть для дроби
Скобке, стоящей в квадрате, всегда соответствуют 2 дроби. Знаменатель одной из них – это скобка в 1-й степени, знаменатель другой – та же скобка в квадрате. Корни знаменателей
(поиск C требует умножения первоначальной дроби на Коэффициент B вычёркиванием найти нельзя – возникнет деление на 0. Чтобы найти B, представим, что будет, если свести всё к общему знаменателю:
Достаточно увидеть, что в числителе появится
и тогда
Здесь Ответ: а) б)
Замечание. Коэффициент B можно найти и другими способами. Так, можно увидеть, что после приведения к общему знаменателю в числителе появится Наконец, можно взять любое число, отличное от уже использованных значений
что равносильно Любой верный способ даёт одно и то же значение коэффициента. Пример 4. Разложим дробь
Так же находим
Чтобы найти A, возьмём любое значение x, кроме –3 и 2, например,
После упрощений Тогда Ответ: а) б) Пример 5. Разложим дробь
Методом вычёркивания можно найти только C:
Можно быстро найти A, если заметить, что в числителе исходной дроби нет слагаемого с
Тогда Коэффициент B также легко найти, если увидеть, что после того же приведения остаются свободные коэффициенты Поэтому
Значит,
Как показано ранее (например, в § 2),
Остальные интегралы – табличные. Ответ:а) б) (модуль заменили простыми скобками, поскольку всегда
В следующем примере просто подставим числа и решим уравнения. Пример 6. Проинтегрируем
Находим
Умножим 1-е уравнение на 9, а 2-е – на –9:
Вычитая одно уравнение из другого, замечаем, что Коэффициент A известен, выгодно выразить Итак,
Ответ: а) б) Замечание. В примере 6 получается довольно простая система уравнений. Иногда выгоднее заменить дроби на десятичные, например,
(где
ИД2. Проинтегрируйте дробь 1) а) a = 0, b = 1, c = 2; б) a = 0, b = 1, c = –1; в) a = 0, b = 2, c = 3; г) a = 1, b = 2, c = 3; д) a = 1, b = 2, c = –3; е) a = –1, b = 2, c = 3; ж) a = 2, b = –2, c = 1; з) a = 2, b = –2, c = –1; и) a = 3, b = 4, c = 5; к) a = 3, b = 4, c = –5; л) a = 3, b = –4, c = 5; м) a = –1, b = –3, c =–5; 2) а) a = 1, b = 2, c = 3; б) a = 1, b = 2, c = –3; в) a = 1, b = –1, c = 2; г) a = 1, b = –1, c = –2; д) a = 1, b = 2, c = –2; е) a = 1, b = –2, c = 3; ж) a = 2, b = 3, c = –4; з) a = 2, b = –3, c = 4; и) a = 3, b = 4, c = –3; к) a = 3, b = 4, c = –4; л) a = 1, b = 3, c = 5; м) a = 1, b = 3, c = –5; 3) а) a = 0, b = 1, c = –1; б) a = 1, b = –1, c = 2; в) a = 1, b = 2, c = –2; г) a = –1, b = 2, c = –2; д) a = 1, b = 2, c = 3; е) a = 1, b = 2, c = –3; ж) a = 1, b = –2, c = 3; з) a = 1, b = –2, c = 3; и) a = –1, b = –2, c = 3; к) a = 3, b = 4, c = 5; л) a = 3, b = –4, c = 5; м) a = 3, b = 4, c = –5. ИД3. Проинтегрируйте дробь 1) а) a = 0, b = 1; б) a = 0, b = –1; в) a = 1, b = 0; г) a = –1, b = 0; д) a = 1, b = –1; е) a = –1, b = 1; ж) a = 0, b = –2; з) a = 2, b = 0; и) a = 1, b = 3; к) a = 3, b = –1; л) a = 3, b = –4; м) a = 4, b = –5; 2) 3)
ИД4. Проинтегрируйте дроби 1) а) a = 1, b = 0; б) a = 1, b = 1; в) a = 1, b = –1; г) a = 1, b = 2; д) a = 1, b = –2; е) a = 2, b = 0; ж) a = 2, b = 1; з) a = 2, b = –1; и) a = 2, b = 2; к) a = 2, b = –2; л) a = 4, b = 3; м) a = 4, b = –3. 2) 3)
ИД5. (*)Проинтегрируйте дроби, разложив их на элементарные. Если необходимо, предварительно получите целую часть и правильную дробь: 1) а) 2) а) 3) а) 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 в точке
в точке 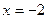 , т.е.
, т.е.  ;
; в точке
в точке  , т.е.
, т.е. 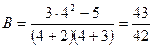 ;
;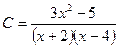 в точке
в точке  , т.е.
, т.е.  .
. .
. .
. .
. указаны m = 2, n = –5, p = 1 и тем самым дана дробь
указаны m = 2, n = –5, p = 1 и тем самым дана дробь  . Все множители – линейные скобки, поэтому
. Все множители – линейные скобки, поэтому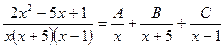 .
. . По аналогии с примером 1:
. По аналогии с примером 1: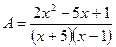 в точке
в точке 

 ;
; в точке
в точке 
 ;
; в точке
в точке 
 .
.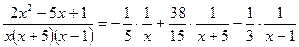 , и соответственно
, и соответственно .
. .
. .
. даны параметры m = 1, n = 0, p = –3. Раскладываем дробь
даны параметры m = 1, n = 0, p = –3. Раскладываем дробь  . Множители в знаменателе линейны, но один из них – в квадрате. В этом случае
. Множители в знаменателе линейны, но один из них – в квадрате. В этом случае .
. . Коэффициенты A и C можно найти методом вычёркивания:
. Коэффициенты A и C можно найти методом вычёркивания: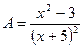 в точке
в точке  ;
; в точке
в точке 

 , а не на
, а не на  ).
).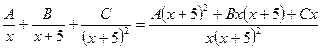 .
. , или
, или  , а по условию в числителе стоит
, а по условию в числителе стоит 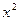 с коэффициентом 1. Значит,
с коэффициентом 1. Значит,  . Подставим
. Подставим  :
:  , откуда
, откуда  . Итак,
. Итак, ,
,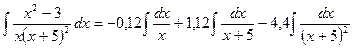 .
. , остальные интегралы – табличные и находятся так же, как в примерах 1 и 2.
, остальные интегралы – табличные и находятся так же, как в примерах 1 и 2. .
. , а в числителе первоначальной дроби x в первой степени отсутствует (т.е. стоит 0x). Тогда из уравнения
, а в числителе первоначальной дроби x в первой степени отсутствует (т.е. стоит 0x). Тогда из уравнения  при
при 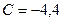 также получается
также получается  , и подставить его в основное равенство:
, и подставить его в основное равенство: ,
, . Поскольку
. Поскольку  находим
находим  . В знаменателе одна из скобок – в квадрате. В этом случае, по аналогии с примером 3,
. В знаменателе одна из скобок – в квадрате. В этом случае, по аналогии с примером 3, .
. при
при  , а именно
, а именно  ;
; при
при  .
. , и подставим в разложение дроби, учитывая, что
, и подставим в разложение дроби, учитывая, что  и
и  :
: .
. , или
, или  . Значит,
. Значит,  (значение точное). Итак,
(значение точное). Итак,  .
. , интегралы находятся так же, как в примере 3.
, интегралы находятся так же, как в примере 3. .
. и проинтегрируем. Один из множителей знаменателя – квадратичное выражение. Согласно общей схеме, в числителе соответствующей дроби пишется не просто коэффициент, а линейная функция относительно x:
и проинтегрируем. Один из множителей знаменателя – квадратичное выражение. Согласно общей схеме, в числителе соответствующей дроби пишется не просто коэффициент, а линейная функция относительно x: .
. при
при 
 .
. :
: .
.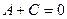 , откуда
, откуда  .
.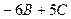 , а в исходной дроби стоит свободный коэффициент –7.
, а в исходной дроби стоит свободный коэффициент –7. , или
, или  , и тогда
, и тогда  . Получили разложение
. Получили разложение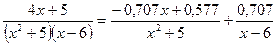 .
. .
. .
.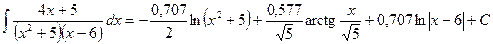
 ).
). . Заметим, что
. Заметим, что 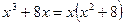 , поэтому
, поэтому .
. – как в предыдущих примерах. Далее подставим
– как в предыдущих примерах. Далее подставим  :
: ;
; .
.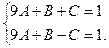
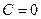 , и тогда
, и тогда  .
.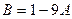 и подставить
и подставить  . Тем самым
. Тем самым  .
. , соответственно
, соответственно .
. ;
;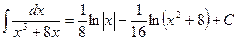 .
.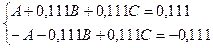
 ), подставить
), подставить  (например, методом Крамера).
(например, методом Крамера).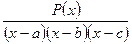 , где числитель
, где числитель  указан, разложив её на сумму
указан, разложив её на сумму 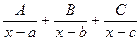 при заданных значениях a, b, c:
при заданных значениях a, b, c: ;
; ;
; ;
; , где числитель
, где числитель  при заданных значениях a, b:
при заданных значениях a, b: ;
; при тех же значениях a, b, что в задании 1;
при тех же значениях a, b, что в задании 1; при тех же значениях a, b, что в заданиях 1 и 2.
при тех же значениях a, b, что в заданиях 1 и 2.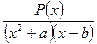 , разложив на сумму дробей
, разложив на сумму дробей  при разных числителях
при разных числителях  ;
; при тех же значениях a, b, что в задании 1;
при тех же значениях a, b, что в задании 1; при тех же значениях a, b, что в заданиях 1 и 2.
при тех же значениях a, b, что в заданиях 1 и 2. ; б)
; б)  ; в)
; в)  ; г)
; г) 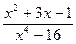 ; д)
; д) 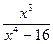 ;
; ; б)
; б) 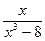 ; в)
; в)  ; г)
; г)  ; д)
; д)  ;
; ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д)
; д)  .
.