
|
|
Замена переменной в неопределённом интегралеИногда удаётся перейти к более простому интегралу, заменив переменную. Пусть дан
Но Для этого некоторую часть функции Фактически интегрирование заменой переменных начинается не с поиска подстановки Пример 1. Найдём Сделаем так: пусть (Вспомним, что
Теперь очень легко раскрыть скобки:
и найти интеграл как сумму двух табличных интегралов:
где Итак, Можно вернуться к исходной переменной:
и даже вынести общий множитель:
но это не всегда легко или целесообразно. ЗМ1. Найдите интегралы, заменив скобку на новую переменную:
Пример 2. Найдём
Интеграл распадается на сумму табличных:
Вынесем за скобку
ЗМ2. Найдите интегралы при помощи подходящей замены знаменателя: 1) 2) 3)
Пример 3.Найдём интеграл
Упростим и вернёмся к старой переменной:
Можно свести к общему знаменателю и найти, что Пример 4.Найдём Подставим:
По отдельности находим а) б) в) тогда
где
В следующих примерах путём замены избавляются от корня. ЗМ3. Найдите интеграл при помощи замены
Пример 5.
Подставим в интеграл:
Здесь 1/4 представили как 0,25 и
Можно вынести корень за скобку, упростить и получить, что
Замечание. Интеграл можно найти и без замен, представив числитель так:
затем сократив ЗМ4. При помощи замены
Пример 6. Чтобы найти
Подставив
находим табличный интеграл и возвращаемся к переменной x:
Ответ:
ЗМ5. При помощи замены
Пример 7. Возьмём
подставим в интеграл: Разложим дробь на целую часть и правильную дробь:
тогда Учтём, что Ответ: Пример 8.Поменяем в примере 7 знак в подкоренном выражении и найдём
поэтому При разложении дроби получим
и отличие от примера 7 окажется в поиске табличного интеграла:
Ответ: ЗМ6. Найдите интегралы 1) 2) 3) 4) Пример 9.
Разбиваем на 2 интеграла, находим по таблице, возвращаемся к переменной x:
Ответ: Пример 10.
Тем самым
Ответ: Модуль в ответе необязателен, поскольку Пример 11. Подставим:
Значит, Ответ: Можно заменять не корень, а весь знаменатель, в котором он находится. Пример 12. Найдём
откуда
Тогда
Интеграл разбивается на 2 простейших, и в результате
Итак, Ответ:
ЗМ7. Найдите интегралы при помощи замены 1) 2) Пример 12. Найдём
ЗМ8.Найдите интегралы
Пример 13. Найдём 1-й способ. Заменим
Известно, что
По таблице (интеграл 2)
Возвращаясь к старой переменной, запишем Ответ: 2-й способ. Заметим, что
Ответтот же, что при решении 1-м способом. Учли, что Кроме того, в интеграле
или же заменить
и найти так, как в § 3. Все ответы будут одинаковы. Интегрирование по частям
Формула интегрирования по частям имеет вид В качестве Оставшаяся часть подынтегрального выражения принимается за Реже применяются формулы
Пример 1.
Подставим в формулу интегрирования по частям:
Интеграл от
Ответ: Пример 2.
Подставим в формулу интегрирования по частям:
Поскольку Ответ: Пример 3.
По той же формуле интегрирования по частям
Но Ответ: Обратите внимание, что константа при интегрировании по частям пишется только на последнем шаге. ИЧ1. Найдите интегралы 1) 2) 3) 4) 5) ИЧ2. Найдите интегралы, дважды выполнив интегрирование по частям: 1) 2) 3) Пример 4. Найдём
Новый интеграл также находится по частям. Теперь
Подставим этот результат вместо
Если вынести за скобку Ответ: Пример 5. Чтобы по частям найти
что равносильно Теперь берём
Но
где
или, после необязательных упрощений, окончательный Ответ:
ИЧ3. Найдите интегралы по частям, выбрав подходящие 1) 2) 3) Пример 6.Найдём Находим
Далее Ответ:
Пример 7. Найдём
где интеграл
Удобно запомнить, что Ответ:
Более сложные интегралы вида 1) заменой 2) выбирают 3) по частям приходят к интегралу 4) берут его по стандартной схеме, приведённой в любом учебнике. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Представим, что аргумент – некоторая функция
. Представим, что аргумент – некоторая функция  . Тогда
. Тогда 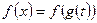 – новая функция от параметра t. Обозначим её как
– новая функция от параметра t. Обозначим её как  . Кроме того,
. Кроме того,  . Подставим:
. Подставим: .
. также новая функция от параметра t, обозначим её как
также новая функция от параметра t, обозначим её как  . Получили новый интеграл
. Получили новый интеграл  . Задача – подобрать замену
. Задача – подобрать замену 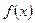 заменяют параметром t:
заменяют параметром t:  , выражают из этого равенства переменную:
, выражают из этого равенства переменную:  .
. . Можно раскрыть 4-ю степень скобки, получить 5 слагаемых, раскрыть произведение двух скобок и проинтегрировать всё, что получится. Очевидно, такой способ несколько громоздок. Тем более неясно, что делать при ещё больших и (или) нецелых степенях.
. Можно раскрыть 4-ю степень скобки, получить 5 слагаемых, раскрыть произведение двух скобок и проинтегрировать всё, что получится. Очевидно, такой способ несколько громоздок. Тем более неясно, что делать при ещё больших и (или) нецелых степенях. , тогда
, тогда 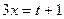 и соответственно
и соответственно 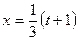 . Также найдём дифференциал:
. Также найдём дифференциал:  .
. .) Подставим:
.) Подставим: .
.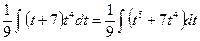
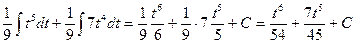 ,
, .
. , где
, где 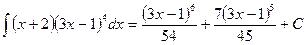
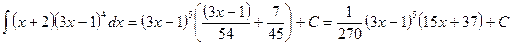 ,
, .
. . Пусть
. Пусть  , тогда
, тогда  и
и 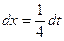 . Также нам понадобится величина
. Также нам понадобится величина  . Подставим в интеграл и сведём к общему знаменателю:
. Подставим в интеграл и сведём к общему знаменателю: .
. , где
, где  .
. и вернёмся к старой переменной:
и вернёмся к старой переменной: .
. ;
; ;
; .
.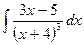 . Заменим
. Заменим  , тогда
, тогда  ,
,  и
и  . Поэтому
. Поэтому .
. .
. .
. . Заменим
. Заменим  . Также
. Также 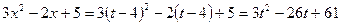 .
. .
. ;
; ;
; (табличный интеграл);
(табличный интеграл);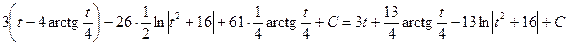 ,
, . Итак,
. Итак,  .
. , выразив
, выразив  , заменив
, заменив  и перейдя к интегралу от переменной t:
и перейдя к интегралу от переменной t: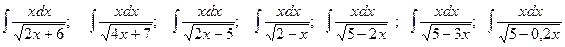 .
. Заменяем:
Заменяем: .
.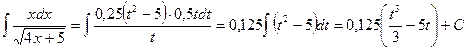 .
. – как
– как  . Учтём, что
. Учтём, что  :
: .
. .
. ,
, и применив основное правило табличного интегрирования. В более сложных интегралах такой способ не поможет.
и применив основное правило табличного интегрирования. В более сложных интегралах такой способ не поможет.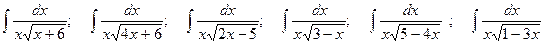 .
. , заменяем:
, заменяем: .
. ,
,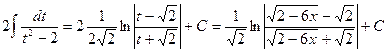 .
. .
. .
. . Заменив
. Заменив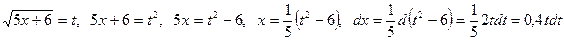 ,
, .
. ,
, .
. . Поскольку
. Поскольку  , запишем
, запишем .
. . Вначале отличия тоже только в знаке:
. Вначале отличия тоже только в знаке: ,
,  ,
,  ,
, .
. ,
, .
. .
. ;
; ;
; ;
;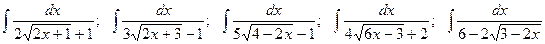 .
. Заменим
Заменим  , тогда
, тогда  и
и 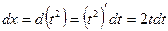 . Подставим:
. Подставим: .
. .
.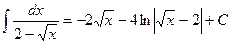 .
. Заменим
Заменим  , тогда
, тогда  , затем
, затем  и
и  . Подставим:
. Подставим: .
. , где
, где  .
. .
. (там, где корень имеет смысл, т.е. при всех
(там, где корень имеет смысл, т.е. при всех  ).
).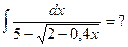 Заменяем
Заменяем  , тогда
, тогда  и
и  , откуда
, откуда  .
.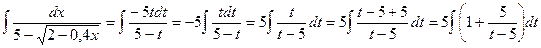 .
. , где
, где  .
. .
. . Пусть
. Пусть 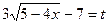 . Выразим x:
. Выразим x: ,
, .
. . Поэтому
. Поэтому .
.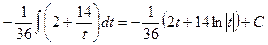 , где
, где  .
. .
. ;
; .
. . Пусть
. Пусть  . В таком случае
. В таком случае .
. .
. . Показательные функции допускают несколько способов замены.
. Показательные функции допускают несколько способов замены. , тогда
, тогда  , поэтому
, поэтому  . При этом
. При этом  . Подставим:
. Подставим: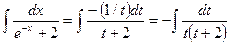 .
. , тогда
, тогда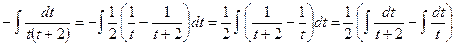 .
. .
. , что равносильно
, что равносильно  .
. . Заменим
. Заменим  , тогда
, тогда  и
и  . Подставим:
. Подставим: .
. при любом x, поэтому модуль можно опустить.
при любом x, поэтому модуль можно опустить. можно вместо замены
можно вместо замены  под знак дифференциала, как в § 2:
под знак дифференциала, как в § 2: ,
, , откуда
, откуда  и
и  , после чего получить
, после чего получить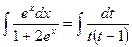
 где
где  – любые функции. Цель её применения – получить интеграл проще исходного и найти его каким-либо способом (например, как табличный).
– любые функции. Цель её применения – получить интеграл проще исходного и найти его каким-либо способом (например, как табличный). берётся функция, производная которой выглядит проще, чем сама
берётся функция, производная которой выглядит проще, чем сама  и от неё берётся интеграл, чтобы восстановить функцию
и от неё берётся интеграл, чтобы восстановить функцию  .
. , а также
, а также , где
, где  .
. Выбираем
Выбираем  , тогда
, тогда  . Необходимо найти
. Необходимо найти  :
: ,
,  .
. .
. уже известен и равен
уже известен и равен  . Значит,
. Значит, .
. (вынесли общий множитель и упростили).
(вынесли общий множитель и упростили). Выбираем
Выбираем  , тогда
, тогда 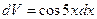 ,
, ,
,  .
. .
. , получаем
, получаем , или
, или  .
. Пусть
Пусть  , тогда
, тогда  , далее
, далее ,
,  .
.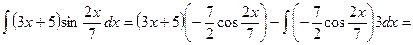
 .
. , и тогда, с заменой
, и тогда, с заменой  на С,
на С,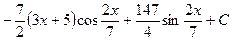 .
.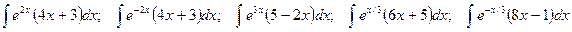 ;
; ;
; ;
; ;
;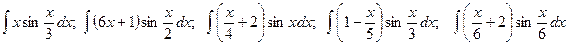 .
. ;
;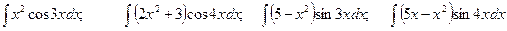 ;
; .
. . Выбираем
. Выбираем  , тогда
, тогда  и
и  , поэтому
, поэтому .
. , соответственно
, соответственно  , и тогда (подразумевая
, и тогда (подразумевая  в будущем ответе)
в будущем ответе) .
. в равенство, полученное на 1-м шаге:
в равенство, полученное на 1-м шаге: .
. и упростить, получим
и упростить, получим .
. , выбираем
, выбираем  и
и  , тогда
, тогда 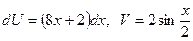 . Значит,
. Значит, ,
, .
. , тогда
, тогда  . Отдельно находим новый интеграл
. Отдельно находим новый интеграл .
.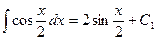 , и поэтому
, и поэтому ,
, . Возвращаясь к предыдущему шагу, получаем, что
. Возвращаясь к предыдущему шагу, получаем, что ,
, .
. :
: ;
; ;
; .
. , для чего запишем его как
, для чего запишем его как 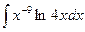 . Под знаком интеграла есть логарифм, именно его следует взять в качестве U:
. Под знаком интеграла есть логарифм, именно его следует взять в качестве U:  . Тогда
. Тогда  .
.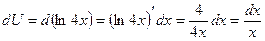 , также
, также 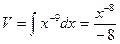 , тогда
, тогда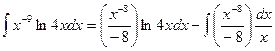 .
. .
. .
. . Берём
. Берём 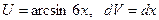 и, очевидно,
и, очевидно,  (постоянную C не пишем). Кроме того,
(постоянную C не пишем). Кроме того,  , тогда
, тогда ,
, можно найти так:
можно найти так: .
. при любом
при любом  . Итак,
. Итак, .
. при
при  обычно находят так:
обычно находят так: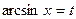 сводят к интегралу
сводят к интегралу  ;
; ,
,  ;
;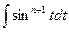 ;
;