
|
|
Подведение под знак дифференциалаФедеральное государственное бюджетное Образовательное учреждение Высшего профессионального образования «Хабаровская государственная академия экономики и права» Кафедра математики и математических методов в экономике Е.А. Мясников ПРАКТИКУМ ПО МАТЕМАТИЧЕСКОМУ АНАЛИЗУ Часть 2
Хабаровск 2012 УДК 51 (075.8) ББК В 11 М 99
Мясников Е. А. Практикум по математическому анализу. Часть 2 : учеб. пособие / Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2012. – 116 с.
Содержание учебного пособия соответствует государственным образовательным стандартам дисциплин «Математика» и «Математический анализ» для бакалаврантов 1-го курса обучения. Предназначено для самостоятельных и аудиторных практических занятий. Включает краткие теоретические сведения, общие схемы решения задач, образцы решения примеров разной сложности, задания для самостоятельной работы. Составлено для бакалаврантов экономических вузов всех направлений подготовки, может быть полезно студентам, обучающимся заочно, и всем, кто желает изучить или повторить курс математики самостоятельно.
Рецензенты: А.Г. Зарубин, д-р. физ.-мат. наук, профессор, зав. каф. прикладной математики и информатики ТОГУ; В.Я. Прудников, канд. физ.-мат. наук, доцент каф. прикладной математики ДВГУПС.
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
© Мясников Е.А., 2012 © Хабаровская государственная академия экономики и права, 2012
Предисловие В пособии представлены темы, изучаемые в экономических вузах во 2-м семестре в курсе математического анализа. Цель пособия – помочь студентам в решении стандартных задач. В 1-й части были изложены основы теории пределов, непрерывности и дифференциального исчисления и методы решения задач по этим темам. Во 2-й части показаны важнейшие способы интегрирования функций и методы решения дифференциальных уравнений. Во 2-й части сохранён тот же принцип, что и в 1-й – постепенное усложнение задач и их строгая систематизация. Двухбуквенный код соответствует параграфу, отдельное задание – очередному вопросу темы, важные частные случаи нумеруются цифрами, однотипные задачи обозначены буквами или просто записаны в одной строке (в случае интегралов). Ответы к I главе даны только в трёх темах, где основная трудность – арифметические вычисления. К дифференциальным уравнениям ответы даны практически полностью, поскольку этот раздел студентам приходится изучать самостоятельно, а основная трудность решения – многочисленные преобразования. Варианты заданий для самостоятельных и контрольных работ не предусмотрены, и при необходимости можно составить задание в виде списка номеров задач. Однако лучше, когда задания составляет преподаватель, непосредственно ведущий занятия в группе – он знает и требования, и уровень подготовки. Цель пособия – не обеспечить преподавателя вариантами, а дать возможность последовательно изложить элементы теории и практического применения математики в работе экономиста. Попытка учесть на лекции все возможные типы задач и тем более рассказать об их решении занимает почти всё время, при этом студенты забывают, о чём вообще шла речь, а преподаватель, ведущий семинар, непременно желает изложить всё «намного проще и понятнее». В результате остаётся забытой важнейшая цель изучения математики –научиться самостоятельно думать и работать. Автор надеется, что пособие поможет преодолеть подобные трудности преподавания и изучения дисциплины. Любые вопросы, замечания и предложения об улучшении пособия можно высказать по адресу: ХГАЭП, ауд. 511, кафедра МММЭ. I. ОСНОВЫ ИНТЕГРИРОВАНИЯ Табличное интегрирование Функция Неопределённый интеграл для функции
поэтому общий вид первообразных для функции Аналогично
Простейшая таблица неопределённых интегралов
Эти интегралы называют табличными. Ни один из них не приводится к другому, но любой интеграл, не учтённый в таблице, либо сводится разными методами к указанным, либо вовсе не выражается в элементарных функциях. Трудность интегрирования по сравнению с дифференцированием связана со значительно меньшим набором свойств и правил. Так, справедливы арифметические свойства интегралов
однако нет (и не может быть) никаких общих формул для интеграла от произведения, частного, а также от сложной функции. Более того, небольшое изменение функции под знаком интеграла (подынтегральной функции) может заметно изменить ответ или даже метод решения. Сравните интегралы а) в) г) В то же время производные от подынтегральных функций находятся одним и тем же способом и внешне почти совпадают. Именно поэтому приходится изучать разные методы интегрирования. Основное правило табличного интегрирования: Пусть
Пример 1. Известно (1-й табличный интеграл), что
Коэффициент a может быть дробным и (или) отрицательным:
Вместо 1/1 можно не указывать ничего, вместо –9/1 записывать –9. Пример 2. По основному правилу табличного интегрирования
Однако
Часто встречается ошибка: интеграл
Продифференцировав и упростив, получим именно
и отличие как раз связано с Другая ошибка – наоборот,
ТИ1.А) Найдите производную; Б) найдите дифференциал функции; В) восстановите функцию; Г) найдите интеграл:
Пример 3. Задание ТИ1 удобно решать так: 1) 2) 3) ТИ2. Найдите неопределённые интегралы от дробных функций, разложив дробь на две дроби, упростив и сведя всё к интегралам от степенных функций: 1) 2) 3) Пример 4. С учётом арифметических свойств неопределённого интеграла, а) б) ТИ3. Таким же образом, как в задании ТИ2, найдите неопределённые интегралы от дробно-иррациональных функций 1) 2) 3) Пример 5. Разложим дробь на сумму или разность функций, тогда а)
б)
Здесь
ТИ4. Проинтегрируйте сумму или разность функций при помощи двух табличных интегралов: 1) 2) 3) 4) 5) Указание к п. 4 и 5: учтите, что
Пример 6. Легко убедиться, что а) б)
При интегрировании дробно-рациональных функций следует помнить, что
и т.п., что нетрудно проверить, взяв производную. На самом деле
что тоже проверяется дифференцированием. Также см. Замечание на стр. 6. ТИ5. Найдите интегралы от функций 1) 2) 3) 4) Пример 7. Согласно таблице интегралов, а) ТИ6. Проинтегрируйте, избавившись от коэффициента перед квадратом: 1) 2) 3) 4) Пример 8. Вынесем коэффициент за скобку, а затем за знак интеграла: а) б) ТИ7. Найдите интегралы 1) 2) Пример 9. По таблице находим, что а) б)
ТИ8. Избавившись от коэффициента перед квадратом, найдите интегралы 1) 2) 3) 4) Пример 10 (здесь а) б)
ТИ9. На основе интеграла 1) 2) 3) 4) Пример 11. Задание ТИ9 решается так: а) б) в)
г)
ТИ10. Зная, что 1) 2) Пример 12. По основному правилу табличного интегрирования а) б) ТИ11. Учитывая, что 1) 2) Пример 13. Проверьте дифференцированием, что а) б) ТИ12. На основе интеграла
Пример 14.
ТИ 13. С учётом формулы
Пример 15.
ТИ14. Зная, что
Пример 16.
ТИ15. Учитывая формулу
Пример 17. ТИ16. На основе табличного интеграла
Пример 18. При помощи производной можно проверить, что а) б) ТИ17. На основе табличного интеграла
Пример 19. Легко видеть, что а) б) ТИ18. Зная, что
Пример 20. Подведение под знак дифференциала Метод подведения под знак дифференциала редко приводится в литературе, поэтому вначале покажем, почему он выгоден. Нередко в подынтегральной функции можно увидеть 2 фрагмента, один из которых похож на производную другого. Например, а) в интеграле б) интеграл в) функция Подобные интегралы часто предлагают находить, заменив новой переменной функцию, производная которой обнаружена. Так, для указанных интегралов а) если
б) поскольку
Более подробно метод замены изложен в § 4. Однако вычисление 3-го интеграла при помощи замены уже связано с трудностями. Пусть, заметив, что Тогда
(
В результате громоздких действий практически всё сократилось и получился простой табличный интеграл. Возникает вопрос, нельзя ли было прийти к нему быстрее, если почти ни одно выражение не понадобилось. Действительно, есть более короткое решение:
тогда, заменив
Таким же образом можно было найти интегралы а)
б) Здесь действия показаны очень подробно, и половину из них можно пропустить. Особенно коротким сделает решение следующая Таблица основных дифференциалов 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2025 stydopedia.ru Все материалы защищены законодательством РФ.
|
 называется первообразной для функции
называется первообразной для функции 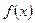 , если
, если 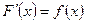 или
или 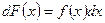 . Например,
. Например, 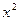 – первообразная для
– первообразная для 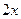 , поскольку
, поскольку  .
.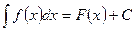 . Константа C подчёркивает, что первообразных для одной и той же функции бесконечно много, но они отличаются только на постоянное число. Например,
. Константа C подчёркивает, что первообразных для одной и той же функции бесконечно много, но они отличаются только на постоянное число. Например,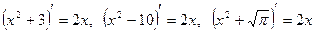 ,
,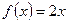 – это
– это 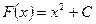 . Значит,
. Значит, 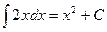 .
.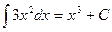 , поскольку не только
, поскольку не только 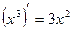 , но и
, но и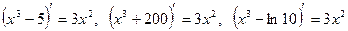 , и т.д.
, и т.д.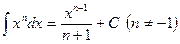 ,
,
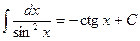 ,
,
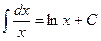 ,
,
 ,
,
 ,
,
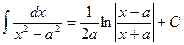 ,
,
 ,
,
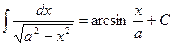 ,
,
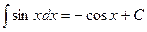 ,
,
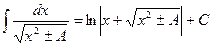 ,
,
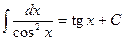 ,
,
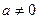 .
.
 ;
; для любого действительного числа
для любого действительного числа 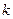 ,
,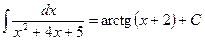 , б)
, б) 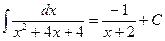 ,
,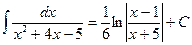 ,
,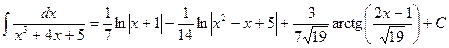 .
.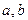 – любые числа и при этом
– любые числа и при этом 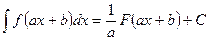 .
.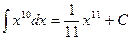 . Тогда
. Тогда
 .
.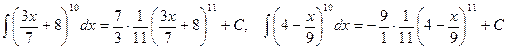 .
. , поскольку
, поскольку 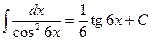 , потому что
, потому что 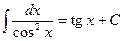 ;
; , так как
, так как 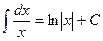 ;
;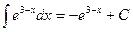 (здесь
(здесь 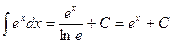 );
);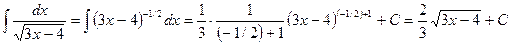 ;
; .
. таким способом не найти: аргумент
таким способом не найти: аргумент  нелинеен относительно х (этот интеграл не выражается в элементарных функциях).
нелинеен относительно х (этот интеграл не выражается в элементарных функциях).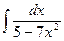 находят как
находят как 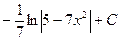 . Правильное решение – свести к интегралу 9 из таблицы:
. Правильное решение – свести к интегралу 9 из таблицы: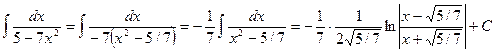 .
. , в то время как
, в то время как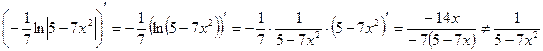 ,
,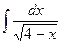 найти как
найти как 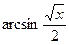 , применив равенство
, применив равенство 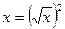 . На самом деле
. На самом деле 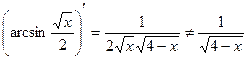 . Правильное решение:
. Правильное решение: 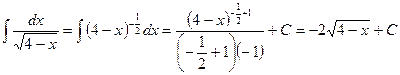 .
.
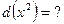
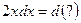
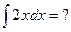
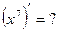
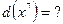
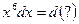
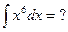
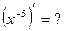

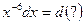
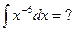
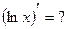
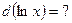
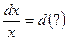
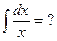
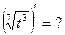


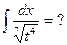
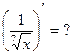

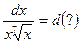
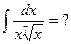
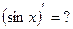
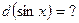


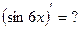
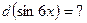
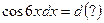
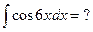
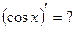
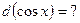
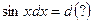
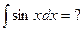

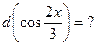
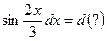
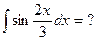
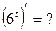
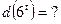
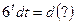
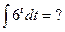
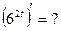

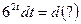
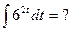
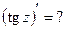
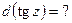

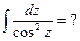


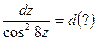

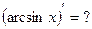
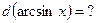
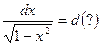

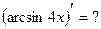
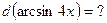
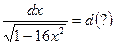

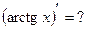
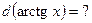
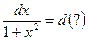
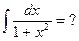
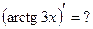
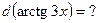

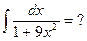
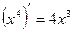 и, как следствие,
и, как следствие, 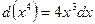 . Тогда
. Тогда 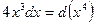 и соответственно
и соответственно 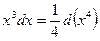 . Также
. Также 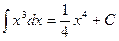 ;
;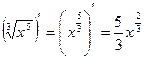 , потому
, потому 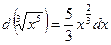 . Наоборот,
. Наоборот, 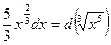 , и тогда
, и тогда 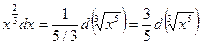 . Кроме того,
. Кроме того, 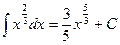 ;
;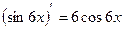 ,
, 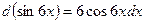 . Тогда
. Тогда 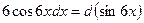 , и потому
, и потому  . Значит,
. Значит, 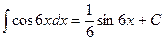 .
.
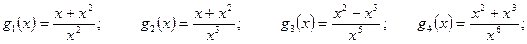
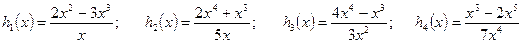 .
.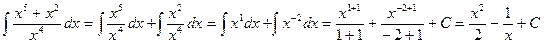 ;
;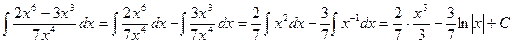 .
.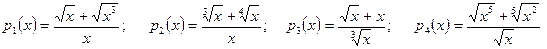 ;
;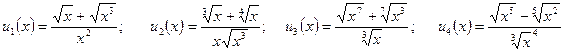 ;
;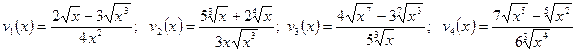 .
.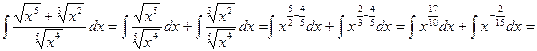
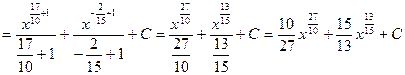 ;
;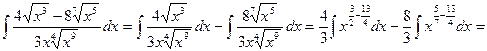
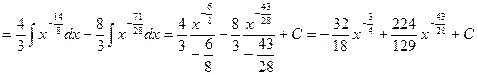 .
.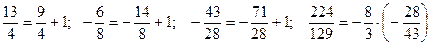 . Также
. Также 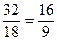 .
.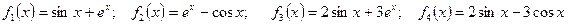 ;
;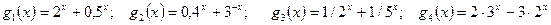 ;
; ;
;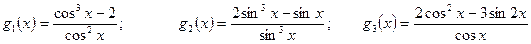 ;
;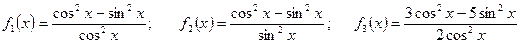 .
.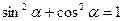 и
и 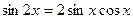 , и сведите всё к одной функции – к
, и сведите всё к одной функции – к  или
или 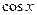 .
.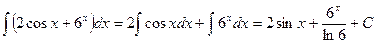 ;
;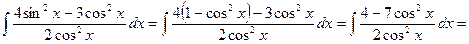
 .
. ;
; 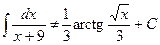 ;
;  ,
,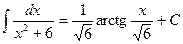 ;
; 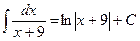 ;
; 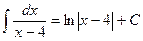 ,
,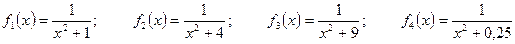 ;
;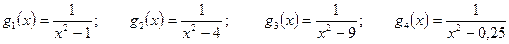 ;
;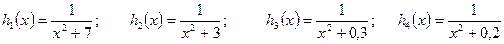 ;
;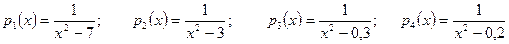 .
.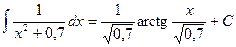 ; б)
; б) 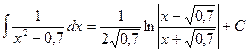 .
.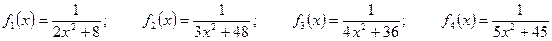 ;
;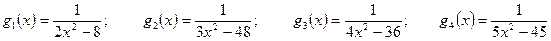 ;
;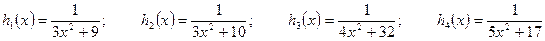 ;
; .
. ;
;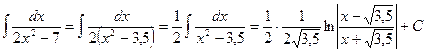 .
.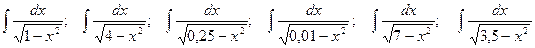 ;
;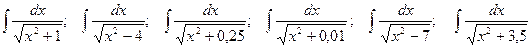 .
.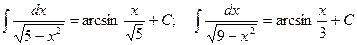 , где
, где  ;
;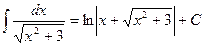 (знак перед числом 3 ни на что не влияет).
(знак перед числом 3 ни на что не влияет). ;
; ;
; ;
;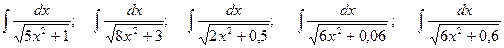 .
. ).
).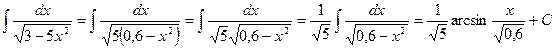 ;
;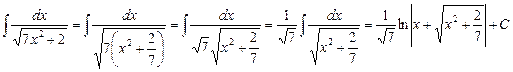 .
.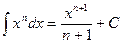 (при
(при 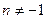 ) найдите
) найдите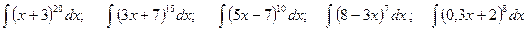 ;
;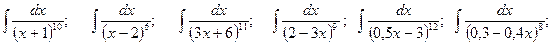
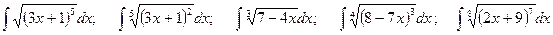 ;
;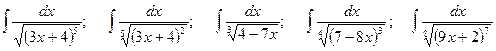 .
.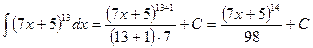 ;
;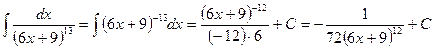 ;
;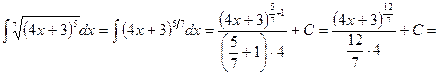
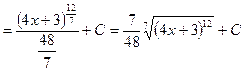 ;
;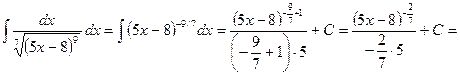
 .
. ;
;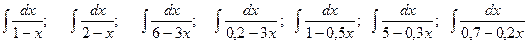 .
.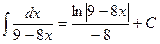 – логарифм знаменателя делим на коэффициент перед переменной;
– логарифм знаменателя делим на коэффициент перед переменной;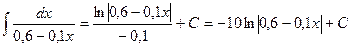 .
.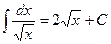 , найдите
, найдите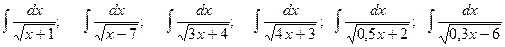 ;
;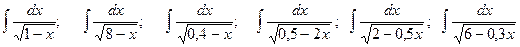 .
.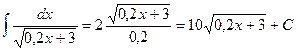 (здесь
(здесь 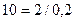 );
);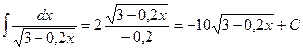 .
.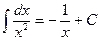 найдите
найдите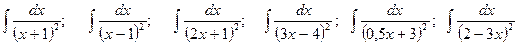 .
. .
.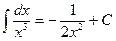 найдите
найдите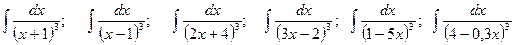 .
. .
.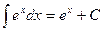 , найдите
, найдите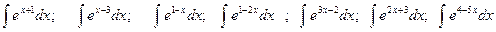 .
. .
.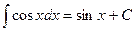 , найдите
, найдите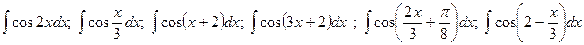 .
.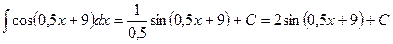 .
. найдите
найдите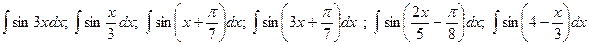 .
.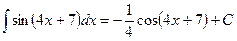 ;
;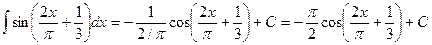 .
.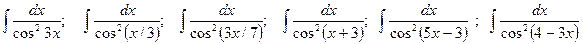 .
.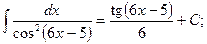
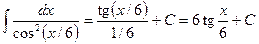 .
.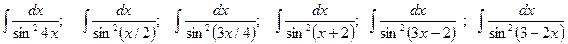 .
. .
.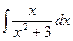 числитель x похож на производную от
числитель x похож на производную от 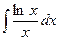 можно представить как
можно представить как 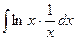 , где
, где 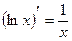 ;
;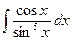 – это
– это 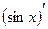 .
. , тогда
, тогда 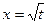 и
и 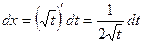 , откуда
, откуда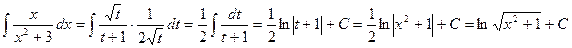 ;
; , то
, то 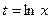 , тогда
, тогда 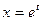 и
и 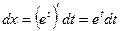 , поэтому
, поэтому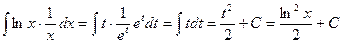 .
. , мы заменили
, мы заменили 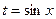 .
.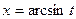 и
и 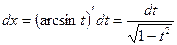 . Выразить
. Выразить 
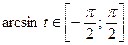 , поэтому
, поэтому  ). Подставим:
). Подставим: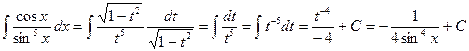 .
.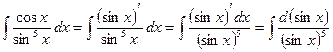 ,
,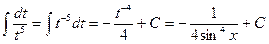 .
.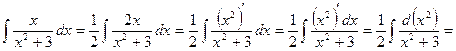
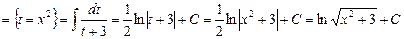 ;
;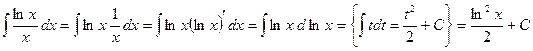 .
.