
|
|
Примеры решения типовых задач
Пример 1. Исследовать на экстремум функцию Решение. Находим частные производные первого и второго порядка: Приравнивая к нулю первые производные, получим систему уравнений для определения стационарных точек:
Решая систему, находим две стационарные точки Вычисляем значения частных производных второго порядка в этих точках:
Затем находим определители:
В силу достаточных условий заключаем, что в точке Пример 2. Найти экстремум функции Решение. Из условия выразим
Мы получили функцию одного переменного. Функция Соответственно,
Пример 3.Найти экстремум функции Решение. Рассмотрим функцию Лагранжа
находим Пример 4. Найти наибольшее и наименьшее значения функции Решение. Находим стационарные точки:
Исследуем данную функцию на границе области, которая представляет собой треугольник На прямой На концах отрезка Аналогично, на прямой
На прямой Сравнивая все полученные значения функции
Задания для самостоятельной работы
22. Исследовать на экстремум следующие функции:
23. Исследовать на условный экстремум следующие функции:
24. Найти наибольшие и наименьшие значения функций, заданных в замкнутой области
14. Подбор эмпирической формулы по методу наименьших
Пусть существует некоторая зависимость между переменными величинами
Требуется найти по данным наблюдений аналитическое выражение Это осуществляется в два этапа. 1. Выяснение общего вида формулы. 2. Определение параметров формулы. Для определения общего вида формулы в декартовой системе координат отмечаются точки Для определения параметров формулы удобно пользоваться методом наименьших квадратов. Сущность этого метода заключается в том, что сумма квадратов отклонений эмпирических значений от теоретических была минимальной:
1. Пусть зависимость между переменными предполагается линейной: Тогда
Упрощая систему получим:
Система (1) называется нормальной системой метода наименьших квадратов при выравнивании по прямой. Решая систему (1) найдём параметры 2. Пусть зависимость между переменными предполагается квадратической: Тогда Найдём минимум функции. Для этого решим систему уравнений:
Система (2) называется нормальной системой метода наименьших квадратов при выравнивании по параболе. Решая систему (2) найдём параметры Рассмотрим на примере. Дана зависимость переменных.
Требуется подобрать зависимость Зависимость между
Первый столбец обозначает номер по порядку записи точек (координат) из суммы столбцов при Решая систему, получим,

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 .
. ;
; 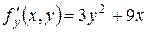 ;
;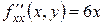 ;
;  ;
;  .
.
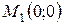 ,
,  .
. ,
,  ,
,  ,
,  ,
,  ,
,  .
.

 нет экстремума, так как
нет экстремума, так как  , а в точке
, а в точке  функция имеет максимум, так как
функция имеет максимум, так как  и
и  , причем
, причем  .
. при
при  условии
условии  .
. и подставим в формулу, задающую функцию:
и подставим в формулу, задающую функцию:  , а потому
, а потому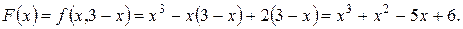
 определена при всех
определена при всех  . Приравнивая к нулю производную, получаем:
. Приравнивая к нулю производную, получаем: 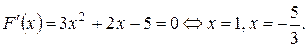 Для найденных значений
Для найденных значений  ; при
; при 
 .
.  при
при  точка
точка  будет точкой минимума исходной функции
будет точкой минимума исходной функции  , а точка
, а точка 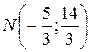 – точкой максимума, т.к. при
– точкой максимума, т.к. при  .
. ,
,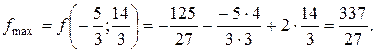
 при условии, что
при условии, что 
 Имеем
Имеем 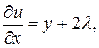
 Из системы уравнений (необходимые условия экстремума)
Из системы уравнений (необходимые условия экстремума)
 . Нетрудно видеть, что в точке
. Нетрудно видеть, что в точке  функция
функция  .
. в области, ограниченной линиями
в области, ограниченной линиями 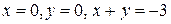 .
.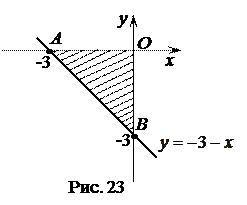
 .
. – стационарная точка,
– стационарная точка,  .
. (рис.23).
(рис.23). :
:  и задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на
и задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на 


 , следовательно
, следовательно  – точка min, в которой
– точка min, в которой  .
. .
. :
: 
 – точка min, в которой
– точка min, в которой  . В точке
. В точке  :
:  .
. , которая задается равенством
, которая задается равенством  , имеем, исключив
, имеем, исключив  в соответствии с уравнением
в соответствии с уравнением  , в которой
, в которой  . На концах
. На концах  – наибольшее значение функции и достигается в точках
– наибольшее значение функции и достигается в точках  ;
;  – наименьшее, в стационарной точке
– наименьшее, в стационарной точке  .
. ;
;
 ;
;
 ;
;
 ;
;
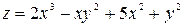 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 , при
, при 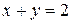 ;
;
 , при
, при  ;
;
 , при
, при  ;
;
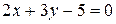 ;
;
 , при
, при  ;
;
 , при
, при  ;
;
 , при
, при  , при
, при  ;
;
 , при
, при  .
.
 :
: ,
, 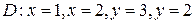 ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
,  ;
;
 ,
, 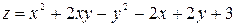 ,
,  .
.






 или
или  . При нахождении этой формулы не требуется, чтобы значения
. При нахождении этой формулы не требуется, чтобы значения  совпадали с
совпадали с 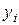 .
. . И определяют, вдоль какой линии они располагаются. Зависимость может быть линейной (вдоль прямой), квадратичной (вдоль параболы), гиперболической, логарифмической, показательной.
. И определяют, вдоль какой линии они располагаются. Зависимость может быть линейной (вдоль прямой), квадратичной (вдоль параболы), гиперболической, логарифмической, показательной. .
. .
. . Найдём минимум этой функции. Для этого решим систему уравнений:
. Найдём минимум этой функции. Для этого решим систему уравнений: .
. (1).
(1).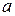 и
и  .
. .
. .
. или
или  (2).
(2). .
.



 . Система имеет вид:
. Система имеет вид:
 и
и  , а уравнение прямой имеет вид:
, а уравнение прямой имеет вид: 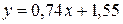 .
.