
|
|
Уравнение прямой, проходящей через две данные точки. Уравнение прямой «в отрезках».Пусть даны две точки М(Х1 ,У1 ) и N(Х2, y2). Найдем уравнение прямой, проходящей через эти точки. Так как эта прямая проходит через точку М, то согласно формуле У – Y1 = K(X – x1), Где K – неизвестный угловой коэффициент. Значение этого коэффициента определим из того условия, что искомая прямая проходит через точку N, а значит, ее координаты удовлетворяют уравнению (1) Y2 – Y1 = K(X2 – X1), Отсюда можно найти угловой коэффициент этой прямой:
Подставим найденное значение K в уравнение (1), и получим
Или после преобразования
Пусть дана прямая
Взаимное расположение прямых. Угол между прямыми. Пусть прямые l1 и l2 относительно прямоугольной декартовой системы координат заданы своими каноническими уравнениями:
Возможны два случая : 1. Прямые Прямые, находясь в одной плоскости, так же могут : 1.1. Совпадать
1.2. Быть параллельными
1.3. Пересекаться не параллельно
1.3.1 Условие перпендикулярности прямых: 2. Прямые Если не выполняется условие 1. Угол между двумя прямыми. Пусть прямые l1 и l2 относительно прямоугольной декартовой системы координат заданы своими каноническими уравнениями:
Полярная система координат. Связь с декартовой системой координат.
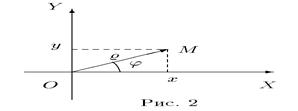
Полярная система координат определяется точкой O, называемой полюсом, и лучом, исходящим из полюса, называемым полярной осью. Полярными координатами ρ и j точки M называются расстояние ρ от полюса до точки M ( ρ = |OM|) и угол j между полярной осью и вектором OM (рис. 2). Угол j называется полярным углом, измеряется в радианах и отсчитывается от полярной оси против часовой стрелки. Полярные координаты точки O: ρ = 0, угол jне определен. У остальных точек ρ > 0 и угол j определен с точностью до 2π. Обычно полагают 0 ≤ j < 2 π или − π < j ≤ π. Если полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс, то декартовы координаты x и y точки M выражаются через ее полярные координаты ρ и j формулами x = ρcosj y = ρsinj . Полярные координаты ρ и j точки M выражаются через ее декартовы координаты x и y формулами:
Замечание. Если не указано положение полюса и полярной оси относительно декартовой системы координат, то считаем, что полюс совпадает с началом прямоугольной декартовой системы координат, а полярная ось — с положительной частью оси абсцисс. Общее уравнение плоскости. Уравнение плоскости «в отрезках». Общим уравнением плоскости называется линейное уравнение первой степени относительно трех переменных: х, у и z, т.е. уравнение вида: Ax + By + Cz + D = 0.
Коэффициенты Частные случаи. 1) Если в уравнении 2) При 3) При Рассмотрим общее уравнение плоскости Ax + By + Cz + D = 0. Перенесем свободный член в правую часть уравнения и разделим обе части уравнения на (–D).
Обозначив
где a, b, c – это отрезки, которые отсекает плоскость от координатных осей.
17. Уравнение плоскости, проходящей через три данные точки. Взаимное расположение плоскостей, угол между плоскостями. Три точки пространства, не лежащие на одной прямой, определяют единственную плоскость. Найдем уравнение плоскости Q, проходящей через три данные точки M1(x1;y1;z1), М2(x2;y2;z2) и М3(х3,y3,z3), не лежащие на одной прямой. Возьмем на плоскости произвольную точку M(x;y;z) и составим векторы
Данное уравнение есть уравнение плоскости, проходящей через три данные точки. Условие параллельности двух плоскостей: Пусть P1:A1x+B1y+C1z+D1=0, P2:A2x+B2y+C2z+D2=0, Плоскости P1 и P2 параллельны тогда и только тогда, когда

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
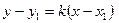 (1)ее уравнение имеет вид:
(1)ее уравнение имеет вид: .
. ,
,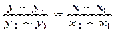 .
.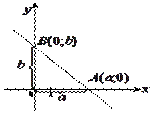
 . Если
. Если  , то, разделив на
, то, разделив на  . Имеем:
. Имеем: 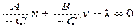 , или
, или 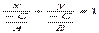 . Обозначив
. Обозначив  ,
, 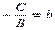 , получим
, получим  – уравнение прямой в отрезках;
– уравнение прямой в отрезках; 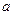 и
и  – отрезки, которые она отсекает на осях координат.
– отрезки, которые она отсекает на осях координат.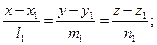


 и
и  лежат в одной плоскости.
лежат в одной плоскости.
 не параллельно
не параллельно 
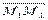
 ,
,  .
.
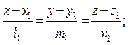



 ;
;  ;
; 

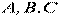 являются координатами нормального вектора плоскости
являются координатами нормального вектора плоскости  . Вектор
. Вектор  перпендикулярен плоскости.
перпендикулярен плоскости. , то плоскость проходит через начало координат.
, то плоскость проходит через начало координат. (
(  ,
,  ) плоскость параллельна оси
) плоскость параллельна оси  (оси
(оси  , оси
, оси  соответственно).
соответственно). (
(  ,
,  ) плоскость параллельна плоскости
) плоскость параллельна плоскости  (плоскости
(плоскости  , плоскости
, плоскости  ).
).

 , получим уравнение плоскости “в отрезках”
, получим уравнение плоскости “в отрезках” ,
, ,
,  ,
,  . Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем
. Эти векторы лежат на плоскости Q, следовательно, они компланарны. Используем условие компланарности трех векторов (их смешанное произведение равно нулю), получаем 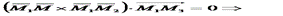 , т. е.
, т. е.
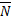 1=(A1,B1,C1);
1=(A1,B1,C1);