
|
|
Векторное произведение векторов и его свойства. Формула для вычисления векторного произведения в декартовой системе координат.Векторным произведением векторов 1) Его модуль равен 2) Вектор 3) Вектор
Векторное произведение векторов
или
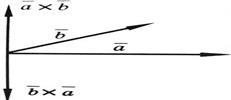
Основные свойства векторного произведения: 1) Векторное произведение 2) При перестановке местами векторов сомножителей векторное произведение меняет знак на противоположный (см. рисунок):
Векторное произведение не обладает свойством переместительности.
3) Скалярным произведением двух векторовна плоскости или в трехмерном пространстве в прямоугольной системе координат называется сумма произведений соответствующих координат векторов То есть, для векторов
Формула скалярного произведения векторов в координатах позволяет заключить, что скалярный квадрат вектора равен сумме квадратов всех его координат: на плоскости Смешанное произведение. Геометрический смысл. Вычисление в декартовых координатах. Смешанное произведение векторов — скалярное произведение вектора Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов. Геометрический смысл смешанного произведения Смешанное произведение Справедливо равенство Необходимым и достаточным условием компланарности трёх векторов является равенство нулю их смешанного произведения. Смешанное произведение трёх векторов, два из которых совпадают, равно нулю. Если три вектора
то смешанное произведение
Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. В декартовых координатах каждая прямая определяется уравнением первой степени и, обратно, каждое уравнение первой степени определяет прямую. Уравнение вида
называется общим уравнением прямой. Угол
Уравнение Если прямая задана общим уравнением
то ее угловой коэффициент определяется по формуле
Уравнение Если прямая проходит через точки
Уравнение
является уравнением прямой, проходящей через две точки Если известны угловые коэффициенты
Признаком параллельности двух прямых является равенство их угловых коэффициентов:
Признаком перпендикулярности двух прямых является соотношение
Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. 
Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
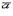 и
и  называется вектор
называется вектор 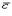 , который определяется следующими условиями:
, который определяется следующими условиями:
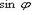 где
где  - угол между векторами
- угол между векторами  и
и  .
.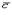 перпендикулярен к плоскости, определяемой перемножаемыми векторами
перпендикулярен к плоскости, определяемой перемножаемыми векторами  и
и  .
. направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы
направлен так, что наблюдателю, смотрящему с его конца на перемножаемые векторы  и
и 
 :
:
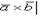


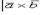


 равно нулю, если векторы
равно нулю, если векторы  и
и  коллинеарны или какой-либо из перемножаемых векторов является нулевым.
коллинеарны или какой-либо из перемножаемых векторов является нулевым.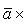





 (распределительное свойство).
(распределительное свойство). и
и  .
. на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид
на плоскости в прямоугольной декартовой системе координат формула для вычисления скалярного произведения имеет вид ,
, , в пространстве
, в пространстве  .
. .
. равно объёму параллелепипеда, построенного на приведённых к общему началу векторах
равно объёму параллелепипеда, построенного на приведённых к общему началу векторах  ,
, 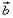 и
и 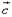 , взятому со знаком плюс, если тройка
, взятому со знаком плюс, если тройка  правая, и со знаком минус, если тройка
правая, и со знаком минус, если тройка  ,
,  и
и 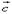 компланарны, то
компланарны, то  равно нулю.
равно нулю.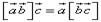 .
. ,
,  и
и  ,
,  ,
,  ,
, равно определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.
равно определителю, строки которого соответственно равны координатам перемножаемых векторов, т.е.

 , определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:
, определяемый, как показано на рис., называется углом наклона прямой к оси Ох. Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой; его обычно обозначают буквой k:

 называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.
называется уравнением прямой с угловым коэффициентом; k - угловой коэффициент, b - величина отрезка, который отсекает прямая на оси Оу, считая от начала координат.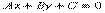 ,
,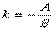 .
. является уравнением прямой, которая проходит через точку
является уравнением прямой, которая проходит через точку 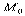 (
( 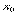 ,
,  ) и имеет угловой коэффициент k.
) и имеет угловой коэффициент k. (
(  ,
,  ),
),  (
(  ,
, 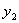 ), то ее угловой коэффициент определяется по формуле
), то ее угловой коэффициент определяется по формуле .
.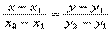
 и
и 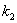 двух прямых, то один из углов
двух прямых, то один из углов  между этими прямыми определяется по формуле
между этими прямыми определяется по формуле .
.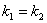 .
. или
или  .
.