
|
|
Задачи контрольной работыВ задачах 3.1.1- 3.1.20 даны координаты вершин треугольника АВС. Найти: · длину стороны АВ; · уравнения сторон АВ и ВС и их угловые коэффициенты; · угол B в радианах; · уравнение медианы АЕ; · уравнение и длину высоты СД; · уравнение окружности, для которой высота СД есть диаметр; · уравнение прямой, проходящей через точку Е параллельно стороне АВ, и точку ее пересечения с высотой СД; · систему линейных неравенств, определяющих треугольник АВС.
Решение типового примера Пример 3.2. Определить вид кривой, построить, найти координаты фокусов и эксцентриситет: Пусть дана кривая Решение: Приведем данное уравнение к каноническому виду. Для этого сгруппируем отдельно члены, содержащие переменные
В каждой из скобок вынесем коэффициент при квадрате переменной, а затем выделим полный квадрат, используя формулы сокращенного умножения
Первые три слагаемые в скобках образуют полный квадрат разности
Аналогичные действия осуществим для переменной
Первые три слагаемые в скобках образуют полный квадрат суммы
Тогда исходное уравнение примет вид:
Введем обозначения:
ПРЕДЕЛЫ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ. Программные вопросы 1) Что называется функцией, числовой последовательностью? 2) Что называется пределом числовой последовательности, функции? 3) Сколько пределов может иметь числовая последовательность? 4) Какие величины называются бесконечно большими, бесконечно малыми? 5) Какая связь существует между бесконечно большими и бесконечно малыми величинами? 6) Какие пределы называют первым и вторым специальными пределами? 7) Какими свойствами обладают пределы? Решение типового примера Пример 4.1.Найти указанные пределы. 1) Решение. 1) Воспользуемся непосредственной подстановкой предельного значения переменной: 2) При непосредственной подстановке получаем неопределенность:
Для того, чтобы избавиться от данного вида неопределенности, разложим числитель и знаменатель дроби, стоящей под знаком предела на множители, используя формулу:
Тогда
Тогда Подставим найденные разложения в исходный предел:
3) При непосредственной подстановке получаем неопределенность:
Для того, чтобы избавиться от данного вида неопределенности, вынесем за скобки в числителе и знаменателе дроби старшую степень переменной:
Так как
Задачи контрольной работы В заданиях 4.1.1 – 4.1.20 найти указанные пределы.
Пример 4.2.Вычислить пределы: а) Решение. а) При непосредственной подстановке получаем неопределенность:
Для того, чтобы избавиться от данного вида неопределенности, домножим числитель и знаменатель дроби, стоящей под знаком предела на величины, сопряженные числителю и знаменателю (т.е. на
б) При непосредственной подстановке получаем неопределенность:
Для того, чтобы избавиться от данного вида неопределенности, введем новую переменную
Однако, непосредственная подстановка опять приводит к неопределенности
в) При непосредственной подстановке получаем неопределенность:
Для того, чтобы избавиться от данного вида неопределенности, домножим и разделим выражение, стоящее под знаком предела на величину, ему сопряженную (т.е. на
Однако, непосредственная подстановка опять приводит к неопределенности

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
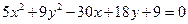 .
. и
и  :
: .
. :
: .
. , следовательно
, следовательно .
. .
. , следовательно
, следовательно .
. ,
, ,
,
 .
. . Произведенную замену будем рассматривать, как преобразование декартовых координат
. Произведенную замену будем рассматривать, как преобразование декартовых координат  в координаты
в координаты  при параллельном сдвиге координатных осей. Причем новое начало координат находится в точке
при параллельном сдвиге координатных осей. Причем новое начало координат находится в точке  . В этой системе координат наше уравнение примет вид:
. В этой системе координат наше уравнение примет вид: .
. Это каноническое уравнение эллипса. Его полуоси
Это каноническое уравнение эллипса. Его полуоси  . Кроме того,
. Кроме того,  , следовательно эксцентриситет
, следовательно эксцентриситет  . остается найти координаты вершин и фокусов эллипса. В новой системе координаты вершин таковы:
. остается найти координаты вершин и фокусов эллипса. В новой системе координаты вершин таковы:  ; координаты фокусов
; координаты фокусов  . Так как старые координаты выражаются через новые по формулам
. Так как старые координаты выражаются через новые по формулам  , то, возвращаясь к первоначальной системе координат получим:
, то, возвращаясь к первоначальной системе координат получим:  ,
,  .
.



















 ; 2)
; 2) 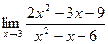 ; 3)
; 3)  .
. .
. .
. , где
, где  - корни соответствующего квадратного уравнения
- корни соответствующего квадратного уравнения  .
. ,
,  ,
, , или
, или  ,
,  .
. или
или  .
. ,
, 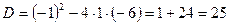 ,
, , или
, или  ,
,  .
. .
. .
. .
. ,
, , то
, то  . Таким образом, после непосредственной подстановки окончательно получаем:
. Таким образом, после непосредственной подстановки окончательно получаем:
 ;
;
 , b)
, b)  , c)
, c)  .
.
 ;
;
 ;
;
 , c)
, c)  ;
;
 , c)
, c)  ;
;
 , c)
, c)  ;
;
 , c)
, c)  ;
;
 , c)
, c)  ;
;
 ;
;
 , c)
, c)  ;
;
 ;
;
 ;
;
 ;
;
 ;
;
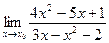 ;
;
 ;
;
 ;
;
 ;
;
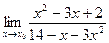 ;
;
 ; б)
; б)  ; в)
; в)  .
. .
. и
и  ):
):

 .
. .
. , где
, где  (т.е
(т.е  есть наименьшее общее кратное показателей радикалов, стоящих в числителе и в знаменателе). В нашем случае
есть наименьшее общее кратное показателей радикалов, стоящих в числителе и в знаменателе). В нашем случае  . Кроме того,
. Кроме того,  следовательно
следовательно  , или
, или  . Таким образом, мы получаем
. Таким образом, мы получаем .
. , которую мы устраним, разложив числитель и знаменатель дроби на множители, используя формулы сокращенного умножения:
, которую мы устраним, разложив числитель и знаменатель дроби на множители, используя формулы сокращенного умножения:
 .
. .
. ):
):
 .
. , которую мы устраним, разделив числитель и знаменатель дроби на
, которую мы устраним, разделив числитель и знаменатель дроби на 
 .
.