
|
|
ЭЛЕМЕНТЫ ВЕКТОРНОЙ АЛГЕБРЫ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕЭлементы векторной алгебры на плоскости Программные вопросы 1. Сумма и разность двух векторов. 2. Коллинеарность и компланарность векторов. 3. Проекция вектора на ось. 4. Разложение вектора в системе орт на плоскости и в пространстве. Координаты вектора. 5. Свойства скалярного произведения векторов. 6. Угол между векторами. Длина вектора по его координатам. 7. Условие перпендикулярности двух векторов. 8. Вектор, перпендикулярный двум данным векторам. 9. Площадь треугольника, построенного на двух векторах. 10. Объём пирамиды с вершинами в заданных точках. Решение типового примера Пример 2.1. Даны координаты точек Требуется: 1) записать векторы 2) найти орт вектора 3) изобразить векторы 4) найти вектора Решение. 1) Известно, что произвольный вектор
где Если заданы точки
Воспользовавшись (2) и координатами точек
Если вектор
Используя формулу (3), получаем длины векторов
2) Известно, что орт вектора
Воспользовавшись формулами (4), получим:
3) Найдем векторы
Таким образом,
Таким образом, Найдем векторы Задачи контрольной работы Даны координаты точек 1) записать векторы 2) найти орт вектора 3) изобразить векторы 4) найти вектора
Элементы векторной алгебры в пространстве Решение типового примера Пример 2.2. Даны координаты вершин пирамиды ABCD. Пусть А(0; 0; 1), В( 2; 3; 5), С(6; 2; 3), D(3; 7; 2). Требуется: 1) Записать векторы 2) Найти угол между векторами 3) Найти проекцию вектора 4) Найти площадь грани АВС; 5) Найти объём пирамиды ABCD; Решение. 1. Известно, что произвольный вектор
где
Если заданы точки
то есть
Воспользовавшись формулой (2) и координатами заданных точек A, B, C, D, получим:
Если вектор
Используя формулу (3), получаем модули найденных векторов:
Известна формула
где
У нас
то есть 3. Известно, что
то есть в нашем случае
4. Воспользуемся формулой нахождения площади треугольника, построенного на векторах
где
В нашем примере
Таким образом,
Объём пирамиды, построенной на трёх некомпланарных векторах
где
У нас
то есть Задачи контрольной работы Даны координаты вершин пирамиды ABCD. Требуется: 1) Записать векторы 2) Найти угол между векторами 3) Найти проекцию вектора 4) Найти площадь грани АВС; 5) Найти объём пирамиды ABCD.
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ 1. Метод координат. Виды уравнений прямой на плоскости. 2. Взаимное расположение 2 – х прямых на плоскости. Угол между 2 – мя прямыми. Условие параллельности и перпендикулярности 2 – х прямых на плоскости. 3. Кривые 2 – го порядка: окружность, эллипс, парабола, гипербола. Решение типового примера Пример 3.1. Даны координаты вершин треугольника ABC: A(4; 3), B(16; - 6), C(20; 16). Найти 1) длину стороны АВ: Расстояние d между двумя точками M1(x1; у1 ) и M2(x2; y2) на плоскости определяется формулой Применяя (1), находим длину стороны АВ: 2) уравнения сторон АВ и ВС и их угловые коэффициенты: Уравнение
является уравнением прямой, проходящей через две точки М1 (x1; y 1) и M 2(x2 ; у2) Подставляя в (2) координаты точек A и B, получим уравнение прямой АВ:
Уравнение y = kx + b называется уравнением прямой с угловым коэффициентом; k — угловой коэффициент, b — величина отрезка, который отсекает прямая на оси Оу, считая от начала координат. Если прямая задана общим уравнением Ах+Ву+С=0, то её угловой коэффициент определяется по формуле k = Решив последнее уравнение относительно y, находим уравнение стороны АВ в виде уравнения прямой с угловым коэффициентом: 4y =-3x+24, или y = - Аналогичным образом, подставляя координаты точек B и C в (2), находим уравнение прямой BC: 11x- 2y -188=0 (ВС) откуда k ВС =
3) угол B: Если известны угловые коэффициенты двух прямых k1 и k2, то один из углов φ между этими прямыми определяется по формуле
Искомый угол В образован прямыми АВ и BC, угловые коэффициенты которых известны из предыдущего пункта. Применяя (3), получим
4) уравнение медианы АЕ: Определим координаты точки Е, которая является серединой отрезка BC по формулам координат середины данного отрезка:
Имеем для точки Е: Подставляя в (2) координаты точек А и Е, находим уравнение медианы АЕ:
5) уравнение и длину высоты СД: Уравнение у — y0 = k(x—х0) (5) является уравнением прямой, которая проходит через точку М0 (х0 ; у0) и имеет угловой коэффициент k. Высота СД перпендикулярна стороне АВ. Воспользуемся условием перпендикулярности 2 – х прямых на плоскости. Признаком перпендикулярности двух прямых является соотношение k1k2= —1 или k2= — Иначе говоря, угловые коэффициенты перпендикулярных прямых обратны по абсолютной величине и противоположны по знаку. Отсюда
kCD= — Подставив в (5) координаты точки С и kCD получим уравнение высоты СD:
у — 16 = Для нахождения длины высоты СD определим координаты точки D как точки пересечения прямых АВ и СD, решив совместно систему уравнений, их задающих:
Откуда x = 8, y = 0, т.е. D (8; 0).
6) уравнение окружности, для которой высота СD есть диаметр; Уравнение окружности с центром в точке О(а; b) радиуса R имеет вид:
(x-a)2+(y-b)2=R2 (6)
Если СD есть диаметр, то центр окружности – точка О – есть середина СD . Используя формулы (4) имеем для О:
Таким образом, О(14; 8).
Если СD есть диаметр, то радиус окружности – есть отрезок СО . Используя (1) найдем радиус:
R= Тогда, (x-14)2+(y-8)2=80 – уравнение искомой окружности.
7) уравнение прямой, проходящей через точку Е параллельно стороне АВ, и точку K ее пересечения с высотой СD: Т.к. заданная прямая параллельна стороне АВ, то можем использовать условие параллельности 2 – х прямых на плоскости: Признаком параллельности двух прямых является равенство их угловых коэффициентов k1 =k2, т.е. k = kAB = -3/4. Знаем, что прямая проходит через точку Е с заданным угловым коэффициентом. Можем использовать уравнение (5):
у — 5 = -3/4(x—18); 4у — 20 = -3(x—18); 3x +4у - 2 = 0. (EL) Точку K пересечения EL с высотой СD найдем, решив совместно систему уравнений, задающих эти прямые:
Откуда, x = 8, y = -88/25, т.е. K (8; -88/25). 8) систему линейных неравенств, определяющих треугольник АВС: Используя неравенство треугольника (сумма двух любых сторон треугольника меньше третьей его стороны), получаем систему:
Из п. 2 известны 3x+4y -24=0 (АВ), 11x- 2y -188=0 (ВС). Запишем уравнение АС, используя (2):
Тогда, система линейных неравенств, определяющих треугольник АВС примет вид:
Или

Не нашли, что искали? Воспользуйтесь поиском по сайту: ©2015 - 2026 stydopedia.ru Все материалы защищены законодательством РФ.
|
 . Пусть
. Пусть  .
. и
и  в системе орт
в системе орт  и найти длины этих векторов;
и найти длины этих векторов; ;
; и
и  аналитически и геометрически.
аналитически и геометрически. представляется в системе орт
представляется в системе орт 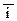 ,
,  по формуле:
по формуле: , (1)
, (1)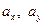 – координаты вектора
– координаты вектора  ,
,  , то для вектора
, то для вектора 
 ,
,  (2)
(2) или
или 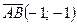 . Тогда
. Тогда  .
. или
или  . Тогда
. Тогда  .
. (3)
(3) и
и  ,
, .
.
 , т.е.
, т.е.  ,
,  (4)
(4)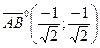 .
.


 .
.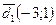 .
.
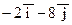 .
. (рис.1).
(рис.1). в системе орт
в системе орт  и найти модули этих векторов;
и найти модули этих векторов; ;
; на вектор
на вектор  ;
; представляется в системе орт
представляется в системе орт 
 (1)
(1) координаты вектора
координаты вектора  в системе координат, порождённой ортами, причём
в системе координат, порождённой ортами, причём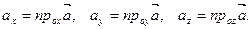
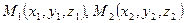 , то для вектора
, то для вектора 

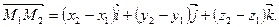 (2)
(2)
 задан формулой (1),то его модуль вычисляется следующим образом:
задан формулой (1),то его модуль вычисляется следующим образом: (3)
(3)

 скалярное произведение векторов
скалярное произведение векторов  , которое можно вычислить следующим образом:
, которое можно вычислить следующим образом:


 .
. ,
,

 векторное произведение векторов, которое можно вычислить по следующему правилу:
векторное произведение векторов, которое можно вычислить по следующему правилу: .
. , причём
, причём
 (кв. ед.).
(кв. ед.). можно найти по формуле
можно найти по формуле
 смешанное произведение векторов, которое вычисляется следующим образом:
смешанное произведение векторов, которое вычисляется следующим образом: .
. , где
, где ,
,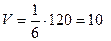 (куб.ед.).
(куб.ед.). (1)
(1)
 (2)
(2) ;
; 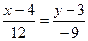 ; 4y-12=-3x+12; или 3x+4y -24=0 (АВ).
; 4y-12=-3x+12; или 3x+4y -24=0 (АВ).
 x+6, откуда k АВ =
x+6, откуда k АВ = 
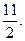
 (3)
(3) = 2.
= 2.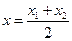 ,
, 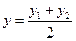 (4)
(4)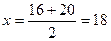 ,
, 
 ;
;  ; x-7y +17=0 (АЕ).
; x-7y +17=0 (АЕ).
 =
= 

 ,
, 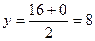 ,
,


 ;
;  ; 13(x-4)=16(y-3); 13x-16y-4=0 (АС).
; 13(x-4)=16(y-3); 13x-16y-4=0 (АС).
